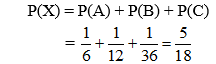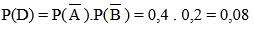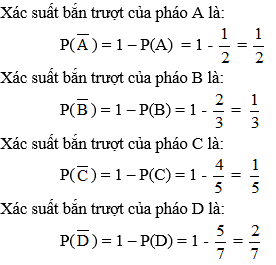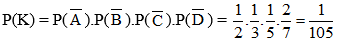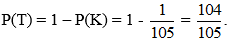30 bài tập biến cố độc lập và biến cố xung khắc 2024 (có đáp án)

Bài tập về biến cố độc lập và biến cố xung khắc

I. Lý thuyết

A. Biến cố độc lập 

1. Định nghĩa:

- Hai biến cố A và B được gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng tới xác suất xảy ra của biến cố kia.

- Nhận xét: Hai biến cố A, B độc lập với nhau thì A và 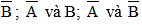 cũng độc lập với nhau.

2. Quy tắc nhân xác suất

- Nếu hai biến cố A và B độc lập với nhau thì

    P(AB) = P(A).P(B)

- Quy tắc nhân xác suất cho nhiều biến cố: Nếu k biến cố A₁, A₂, …,A₃ độc lập với nhau thì

    P(A₁ A₂…A_k) = P(A₁).P(A₂) … P(A_k)

B. Biến cố xung khắc

1. Định nghĩa

- Định nghĩa: Cho hai biến cố A và B. Hai biến cố A và B được gọi là xung khắc nếu biến cố này xảy ra thì biến cố kia không xảy ra.

- Hai biến cố A và B là hai biến cố xung khắc nếu và chỉ nếu Ω_A ∩ Ω_B = ∅.

2. Quy tắc cộng xác suất

- Nếu hai biến cố A và B xung khắc thì xác suất để A hoặc B xảy ra là

    P(A ∪ B) = P(A) + P(B)

- Quy tắc cộng xác suất cho nhiều biến cố:

Cho k biến cố A₁, A₂, …, A_k đôi một xung khắc. Khi đó

    P(A₁ ∪ A₂ ∪ … ∪ A_k) = P(A₁) + P(A₂) + … + P(A_k)

II. Ví dụ minh họa

Ví dụ 1. Tung một con xúc xắc, gọi A là biến cố: “Xuất hiện mặt có chấm số chấm lớn hơn hoặc bằng 4”, B là biến cố: “Xuất hiện mặt có chấm số chấm nhỏ hơn hoặc bằng 2”.

Ta thấy hai biến cố và không cùng xảy ra, do đó A và B là hai biến cố xung khắc.

Ví dụ 2. Một hộp đựng 4 viên bi xanh,3 viên bi đỏ và 2 viên bi vàng.Chọn ngẫu nhiên 2 viên bi. Tính xác suất để chọn được hai viên bi cùng màu.

Hướng dẫn:

Có tất cả: 4 + 3 + 2 = 9 viên bi

X là biến cố “Chọn được 2 bi cùng màu”

Suy ra X = A ∪ B ∪ C và A, B, C là các biến cố đôi một xung khắc.

Theo quy tắc cộng xác suất

Ví dụ 3. Một chiếc máy bay có hai động cơ I và II hoạt động độc lập với nhau. Xác suất để động cơ I và động cơ II chạy tốt lần lượt là 0,6 và 0,8. Hãy tính xác suất để

a) Cả hai động cơ đều chạy tốt

b) Cả hai động cơ đều chạy không tốt

Hướng dẫn

a) Gọi A là biến cố: “Động cơ I chạy tốt”

B là biến cố: “Động cơ II chạy tốt”

C là biến cố: “Cả hai động cơ đều chạy tốt”

Khi đó: C = AB

Vì hai động cơ I và II hoạt động độc lập nên A và B là hai biến cố độc lập.

Áp dụng quy tắc nhân xác suất cho hai biến cố độc lập, ta có

    P(C) = P(A).P(B) = 0,6 . 0,8 = 0,48

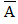
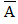
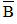
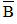
b)  là biến cố đối của biến cố A ⇒ P() = 1 – P(A) = 1 – 0,6 = 0,4

 là biến cố đối của biến cố B ⇒ P() = 1 – P(B) = 1 – 0,8 = 0,2

Gọi D là biến cố: “Cả hai động cơ đều chạy không tốt”

Suy ra D = 

Vì A và B là hai biến cố độc lập nên 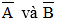 là hai biến cố độc lập.

Áp dụng quy tắc nhân xác suất cho hai biến cố độc lập, ta có

III. Bài tập vận dụng

Câu 1. Bốn khẩu pháo cao xạ A, B, C, D cùng bắn độc lập vào một mục tiêu. Biết xác suất bắn trúng của các khẩu pháo tương ứng là 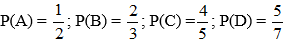. Tính xác suất để mục tiêu bị bắn trúng.

Hướng dẫn

Vì A, B, C, D cùng bắn độc lập nên ta có xác suất mục tiêu không bị bắn trúng là 

Vậy xác suất để mục tiêu bị bắn trúng là

Câu 2. Cho hai biến cố A và B. biết P(A) = 0,21; P(B) = 0,11 và P(A ∪ B) = 0,3. Hỏi A và B có phải là hai biến cố xung khắc không?

Hướng dẫn:

Ta có: P(A) + P(B) = 0,21 + 0,11 = 0,32 ≠ 0,3 = P(A ∪ B)

Suy ra P(A) + P(B) ≠ P(A ∪ B)

Theo quy tắc cộng xác suất của hai biến cố xung khắc, vậy hai biến cố A và B không xung khắc.

Câu 3: Cho P(A) = 0,4; P(B) = 0,5; P(A ∪ B) = 0,6. Hỏi A và B có độc lập hay không?

Hướng dẫn giải:

P(A ∩ B) = P(A) + P(B) – P(A ∪ B) = 0,3 ≠ P(A).P(B) = 0,2.

Vậy A và B không độc lập.

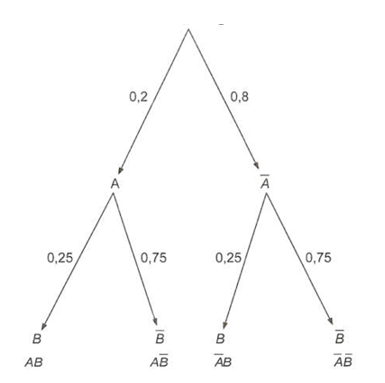
Câu 4: Hai bạn An và Bình không quen biết nhau và đều học xa nhà. Xác suất để bạn An về thăm nhà vào ngày Chủ nhật là 0,2 và của bạn Bình là 0,25. Dùng sơ đồ hình cây để tính xác suất vào ngày Chủ nhật:

a) Cả hai bạn đều về thăm nhà.

b) Có ít nhất một bạn về thăm nhà.

c) Cả hai bạn đều không về thăm nhà.

d) Chỉ có bạn An về thăm nhà.

e) Có đúng một bạn về thăm nhà.

Hướng dẫn giải:

Gọi A và B lần lượt là các biến cố: "Bạn An về thăm nhà vào ngày Chủ nhật" và "Bạn Bình về thăm nhà vào ngày Chủ nhật". A và B là hai biến cố độc lập.

Khi đó $\overline{A}$ là biến cố "Bạn An không về thăm nhà vào ngày Chủ nhật" và $\overline{B}$ là biến cố "Bạn Bình không về thăm nhà vào ngày Chủ nhật".

Ta có sơ đồ hình cây:

a) Cả hai bạn đều về thăm nhà.

P(A ∩ B) = P(AB) = 0,2.0,25 = 0,05.

b) Có ít nhất một bạn về thăm nhà.

P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 0,2 + 0,25 – 0,05 = 0,4.

c) Cả hai bạn đều không về thăm nhà.

$P(\overline{A}\cap \overline{B})=P\left(\overline{A}\overline{B}\right)$ = 0,8.0,75 = 0,6.

d) Chỉ có bạn An về thăm nhà.

$P(A\cap \overline{B})=P\left(A\overline{B}\right)$ = 0,2.0,75 = 0,15.

e) Có đúng một bạn về thăm nhà.

$P(A\overline{B }\cup \overline{A}B)=P\left(A\overline{B}\right)+P\left(\overline{A}B\right)$ = 0,2.0,75 + 0,8.0,25=0,35.

Câu 5. Cho A và B là hai biến cố độc lập.

a) Biết P(A) = 0,3 và P(B) = 0,7. Hãy tính xác suất của các biến cố AB, $\overline{A}B$ và $\overline{A}\overline{B}$.

b) Biết P(A) = 0,8 và P(AB) = 0,4. Hãy tính xác suất của các biến cố B, $\overline{A}B$ và $\overline{A}\overline{B}$.

Hướng dẫn giải:

a) Do A và B là hai biến cố độc lập nên xác suất của biến cố AB là

P(AB) = P(A).P(B) = 0,3.0,7 = 0,21.

Vì $\overline{A}$ là biến cố đối A nên $P\left(\overline{A}\right)=1-P\left(A\right)=0,7$.

Do $\overline{A}$ và B là hai biến cố độc lập nên xác suất của biến cố $\overline{A}B$ là

$P\left(\overline{A}B\right)=P\left(\overline{A}\right).P\left(B\right)=0,7.0,7=0,49.$

Vì $\overline{B}$ là biến cố đối của B nên $P\left(\overline{B}\right)=1-P\left(B\right)=0,3.$

Do $\overline{A}$ và $\overline{B}$ là hai biến cố độc lập nên xác suất của biến cố $\overline{A}\overline{B}$ là

$P\left(\overline{A}\overline{B}\right)=P\left(\overline{A}\right).P\left(\overline{B}\right)=0,7.0,3=0,21.$

b) Do A và B là hai biến cố độc lập nên $P\left(B\right)=\frac{P\left(AB\right)}{P\left(A\right)}=\frac{0,4}{0,8}=0,5.$

Vì $\overline{A}$ à biến cố của A nên $P\left(\overline{A}\right)=1-P\left(A\right)=0,2$.

Do $\overline{A}$ và B là hai biến cố độc lập nên xác suất của biến cố $\overline{A}B$ là

$P\left(\overline{A}B\right)=P\left(\overline{A}\right).P\left(B\right)=0,2.0,5=0,1.$

Vì $\overline{B}$ là biến cố đối của B nên $P\left(\overline{B}\right)=1-P\left(B\right)=0,5.$

Do $\overline{A}$ và $\overline{B}$ là hai biến cố độc lập nên xác suất của biến cố $\overline{A}\overline{B}$ là

$P\left(\overline{A}\overline{B}\right)=P\left(\overline{A}\right).P\left(\overline{B}\right)=0,2.0,5=0,1.$

Câu 6. Có hai lọ hoa. Lọ I cắm 5 bông hoa hồng và 3 bông hoa cúc. Lọ II cắm 4 bông hoa hồng và 5 bông hoa thược dược. Lấy ngẫu nhiên đồng thời từ mỗi lọ một bông hoa. Xét hai biến cố sau:

A: "Lấy được bông hoa hồng từ lọ I", B: "Lấy bông hoa hồng từ lọ II".

Chứng tỏ rằng A và B độc lập.

Hướng dẫn giải:

Dù A có xảy ra (lấy được bông hoa hồng) hay A không xảy ra (lấy được bông hoa cúc) ta đều có P(B) = $\frac{4}{9}$.

Dù B có xảy ra (lấy được được bông hoa hồng) hay B không xảy ra (lấy được bông hoa thược dược) ta đều có P(A) = $\frac{5}{8}$.

Do đó việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra của biến cố kia.

Vậy A và B độc lập.

Câu 7. Một hộp có 7 viên bi màu xanh và 8 viên bi màu đỏ, các viên bi có kích thước và khối lượng như nhau. Lấy viên bi ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên một viên bi trong hộp, ghi lại màu của viên bi lấy ra và bỏ lại viên bi đó vào hộp. Xét các biến cố:

A: “Viên bi màu đỏ được lấy ra ở lần thứ nhất”;

B: “Viên bi màu xanh được lấy ra ở lần thứ hai”.

Hai biến cố A và B có độc lập không? Vì sao?

Hướng dẫn giải:

Trước hết, xác suất của biến cố B khi biến cố A xảy ra bằng $\frac{7}{15}$, xác suất của biến cố B khi biến cố A không xảy ra cũng bằng $\frac{7}{15}$. Do đó việc xảy ra hay không xảy ra của biến cố A không làm ảnh hưởng đến xác suất xảy ra của biến cố B. Mặt khác, xác suất của biến cố A bằng $\frac{8}{15}$, không phụ thuộc vào việc xảy ra hay không xảy ra của biến cố B.

Vậy hai biến cố A và B là độc lập.

Câu 8. Trong một hộp có 8 viên bi xanh và 6 viên bi đỏ. Lấy ngẫu nhiên 2 viên bi trong hộp. Gọi A là biến cố: "Cả hai viên bi có màu xanh"; B là biến cố: "Có một viên bi màu xanh và một viên bi màu đỏ".

a) Tính P(A) và P(B).

b) Tính xác suất để trong hai viên bi lấy ra có ít nhất một viên bi màu xanh.

Hướng dẫn giải:

a) Ta có: $n\left(\Omega \right)=C_{14}^2=91; n\left(A\right)=C_8^2=28;$ n(B) = 8.6 = 48

Vậy $P\left(A\right)=\frac{28}{91}=\frac{4}{13}, P\left(B\right)=\frac{48}{91}.$

b) Xét biến cố C: "Trong hai viên bi lấy ra có ít nhất một viên bi màu xanh", nên C là biến cố hợp của A và B.

Do A và B là hai biến cố xung khắc nên P(C) = P(A) + P(B) = $\frac{28}{91}+\frac{48}{91}=\frac{76}{91}$

Vậy P(C) = $\frac{76}{91}$.

Câu 9. Trong một căn phòng có 36 người, trong đó có 25 người họ Nguyễn và 11 người họ Trần. Chọn ngẫu nhiên hai người trong phòng đó. Tính xác suất để hai người được chọn có cùng họ.

Hướng dẫn giải:

Xét các biến cố sau:

A: "Cả hai người được chọn đều họ Nguyễn"; B: "Cả hai người được chọn đều họ Trần".

C: "Cả hai người được chọn có cùng họ". Khi đó C là biến cố hợp của A và B.

Do A và B xung khắc nên P(C) = P(A ∪ B) = P(A) + P(B).

Ta có: $n\left(\Omega \right)=C_{36}^2=630; n\left(A\right)=C_{25}^2=300; n\left(B\right)=C_{11}^2=55.$

Suy ra P(A) = $\frac{300}{630}$; P(B) = $\frac{55}{630}$

Vậy P(C) = P(A) + P(B) = $\frac{300}{630}+\frac{55}{630}=\frac{71}{126}.$

Câu 10: Hai bạn Sơn và Tùng, mỗi bạn gieo đồng thời hai đồng xu cân đối. Xét hai biến cố sau:

E: “Cả hai đồng xu bạn Sơn gieo đều ra mặt sấp”.

F: “Hai đồng xu bạn Tùng gieo có một sấp, một ngửa”.

Chứng tỏ rằng E và F độc lập.

Lời giải:

Ta có $\Omega$ = {SS; SN; NS; NN}, n($\Omega$) = 4.

E = {SS}, n(E) = 1, suy ra P(E) = $\frac{1}{4}$.

F = {SN; NS}, n(F) = 2, suy ra P(F) = $\frac{2}{4}=\frac{1}{2}$ .

Nếu F xảy ra thì P(E) = $\frac{1}{4}$ ; nếu F không xảy ra thì P(E) = $\frac{1}{4}$.

Nếu E xảy ra thì P(F) = $\frac{1}{2}$ ; nếu E không xảy ra thì P(F) = $\frac{1}{2}$.

Việc xảy ra hay không xảy ra của biến cố này không ảnh hưởng tới xác suất xảy ra của biến cố kia.

Vậy E và F độc lập.

Xem thêm các dạng câu hỏi và bài tập liên quan khác:

175 Bài tập về xác suất của biến cố (có đáp án năm 2023)

70 Bài tập về phép thử và biến cố (có đáp án năm 2023)

50 Bài tập về Xác định biến cố và tính xác suất của biến cố (2024) mới nhất có đáp án 

85 Bài tập về nhị thức Niu-tơn (có đáp án năm 2023)

70 Bài tập về một số phương trình lượng giác thường gặp (có đáp án năm 2024)