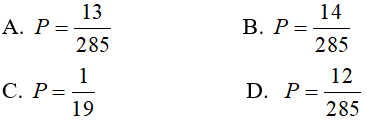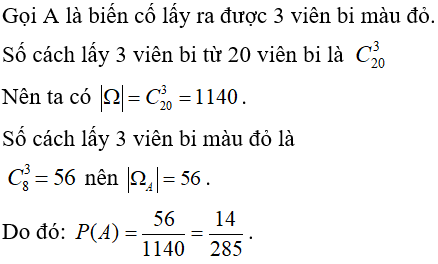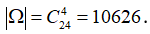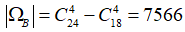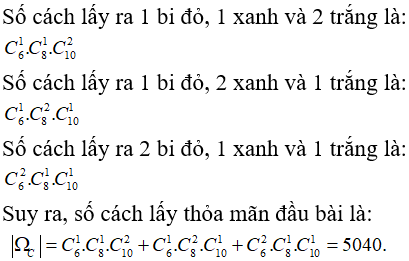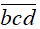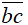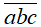Bài giảng Toán 11 Bài 4: Phép thử và biến cố
Kiến thức cần nhớ
I. Phép thử, không gian mẫu
1. Phép thử.
Một trong những khái niệm cơ bản của lí thuyết xác suất là phép thử. Một thí nghiệm, một phép đo, hay một sự quan sát hiện tượng nào đó… được hiểu là phép thử.
- Ví dụ 1. Gieo ba đồng tiền xu liên tiếp, chọn ba cây tú lơ khơ từ bộ bài 52 cây tứ lơ khơ, chọn 3 bông hoa từ 10 bông hoa trong lọ… đây đều là phép thử.
- Khi gieo một đồng tiền, ta không thể đoán trước được mặt xuất hiện là sấp hay ngửa. Đó là ví dụ về phép thử ngẫu nhiên.
- Tổng quát. Phép thử ngẫu nhiên là phép thử mà ta không đoán trước được kết quả của nó, mặc dù đã biết tập hợp tất cả các kết quả có thể có của phép thử đó.
2. Không gian mẫu.
Tập hợp các kết quả có thể xảy ra của một phép thử được gọi là không gian mẫu của phép thử và kí hiệu là (đọc là ô-mê-ga).
- Ví dụ 2. Nếu phép thử là gieo một con súc sắc một lần, thì không gian mẫu gồm 6 phần tử là: = {1; 2; 3; 4; 5; 6}.
- Ví dụ 3. Nếu phép thử là gieo một đồng tiền ba lần thì không gian mẫu gồm tám phần tử là:
{SSS; SSN; SNS; SNN; NSS; NSN; NNS; NNN} .
II. Biến cố.
- Một cách tổng quát, mỗi biến cố liên quan đến một phép thử được mô tả bởi một tập con của không gian mẫu.
- Định nghĩa: Biến cố là một tập con của không gian mẫu.
Ta thường kí hiệu các biến cố bằng các chữ in hoa A; B; C…
- Tập được gọi là biến cố không thể (gọi tắt là biến cố không). Còn tập được gọi là biến cố chắc chắn.
- Ví dụ 4. Gieo con súc sắc liên tiếp hai lần thì biến cố: “lần thứ nhất ra mặt 5 chấm, lần thứ 2 ra mặt 8 chấm” là biến cố không. (vì súc sắc không có mặt 8 chấm)
Còn biến cố: “Tổng số chấm hai lần gieo lớn hơn 1 và nhỏ hơn 13” là biến cố chắc chắn.
- Ta nói rằng biến cố A xảy ra trong một phép thử nào đó khi và chỉ khi các kết quả của phép thử đó là một phần tử của A (hay thuận lợi cho A).
Như vậy, biến cố không thể không bao giờ xảy ra. Trong khi đó, biến cố chắc chắn luôn luôn xảy ra.
III. Phép toán trên các biến cố.
Giả sử A là biến cố liên quan đến một phép thử
- Tập \A được gọi là biến cố đối của biến cố A, kí hiệu là .
xảy ra khi và chỉ khi A không xảy ra.
- Ví dụ 5. Nếu phép thử là chọn một học sinh trong lớp làm lớp trường thì:
Biến cố A: “bạn đó là nữ”.
Biến cố B: “bạn đó là nam”.
Ta thấy, B là biến cố đối của biến cố A: .
- Giả sử A và B là hai biến cố liên quan đến một phép thử. Ta có định nghĩa:
Tập được gọi là hợp của các biến cố A và B.
Tập được gọi là giao của các biến cố A và B.
Nếu thì ta còn nói A và B xung khắc.
- Biến cố xảy ra khi và chỉ khi A xảy ra hoặc B xảy ra.
Biến cố xảy ra khi và chỉ khi A và B đồng thời xảy ra.
Biến cố còn được viết là A.B.
A và B xung khắc khi và chỉ khi chúng không khi nào cùng xảy ra.
- Ta có bảng sau:
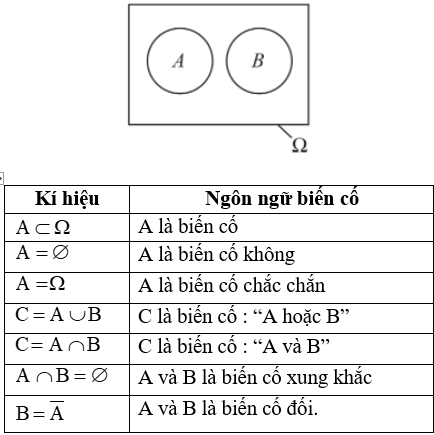
- Ví dụ 6. Xét phép thử: gieo súc sắc hai lần liên tiếp, với các biến cố:
A: “Kết quả hai lần gieo giống nhau”.
B. “Lần đầu xuất hiện mặt 5 chấm”.
Liệt kê các kết quả thuận lợi cho các biến A và B.
Lời giải:
A = {(1; 1); (2; 2); (3; 3); (4; 4); (5; 5); (6; 6)}.
B = {(5; 1); (5; 2); (5; 3); (5; 4); (5; 5); (5; 6)}.
Các dạng toán về phép thử và biến cố
Dạng toán 1. Xác định không gian mẫu của phép thử và các phần tử của không gian mẫu.
Phương pháp:
+ Xác định phép thử
+ Mô tả các kết quả xuất hiện trong phép thử bằng cách sử dụng các phép đếm (quy tắc cộng, quy tắc nhân) hoán vị, chỉnh hợp, tổ hợp, từ đó xác định được không gian mẫu và tính được số phần tử của không gian mẫu.
Dạng 2. Bài tập xác định biến cố và liệt kê các kết quả thuận lợi của biến cố.
Phương pháp:
Giả sử T là phép thử có không gian mẫu là . Gọi là một tập con nào đó của
+ Mỗi khả năng của phép thử T có kết quả được mô tả bởi được gọi là một biến cố A liên quan đến phép thử T (hay biến cố A trong phép thử T).
+ Biến cố A xảy ra khi và chỉ khi kết quả của T thuộc tập
+ Mỗi phần tử của được gọi là một kết quả thuận lợi cho A.
Bài tập tự luyện
I. Bài tập trắc nghiệm
Bài 1: Cho hai đường thẳng song song a và b. Trên đường thẳng a lấy 6 điểm phân biệt. Trên đường thẳng b lấy 5 điểm phân biệt. Chọn ngẫu nhiên 3 điểm. Xác định số phần tử của biến cố A: "Ba điểm được chọn tạo thành một tam giác".
A. 135
B. 165
C. 990
D. 360
Lời giải:
Bài 2: Có ba chiếc hộp: hộp thứ nhất chứa 6 bi xanh được đánh số từ 1 đến 6, hộp thứ hai chứa 5 bi đỏ được đánh số từ 1 đến 5, hộp thứ ba chứa 4 bi vàng được đánh số từ 1 đến 4. Lấy ngẫu nhiên ba viên bi. Tính số phần tử của biến cố A: "Ba bi được chọn vừa khác màu vừa khác số"
A. 120
B. 64
C. 60
D. 84
Lời giải:
Ba bi khác màu nên phải chọn từ mỗi hộp 1 viên bi.
Chọn từ hộp thứ ba 1 viên: có 4 cách chọn.
Chọn từ hộp thứ hai 1 viên có số khác với viên bi đã chọn từ hộp ba: có 4 cách chọn
Chọn từ hộp thứ nhất 1 viên bi có số khác với số của hai viên đã chọn từ hộp một và hai: có 4 cách chọn.
Vậy |ΩA| = 43 = 64.
Bài 3: Một nhóm bạn có 4 bạn gồm 2 bạn nam Mạnh, Dũng và hai nữ là Hoa, Lan được xếp ngẫu nhiên trên một ghế dài. Kí hiệu (MDHL) là cách sắp xếp theo thứ tự: Mạnh, Dũng, Hoa, Lan
a) Tính số phần tử của không gian mẫu
A. 6
B. 24
C. 1
D. 4
b) Xác định biến cố M:”xếp hai nam ngồi cạnh nhau”
A. M={(MDHL),(HMDL),(HLMD)}
B. M={(MDHL),(LMDH),(LHMD)}
C. M={(MDHL),(MDLH),(HMDL),(LMDH),(HLMD),(LHMD)}
D. M={(MDHL),(DMHL),(MDLH),(DMLH),(HMDL),(HDML),(LMDH),(LDMH),(HLMD),(HLDM),(LHMD),(LHDM)}
c) Tìm số phần tử của biến cố N:”xếp nam và nữ ngồi xen kẽ nhau”
A. 24
B. 4
C. 8
D. 6
Lời giải:
a. Mỗi cách sắp xếp 4 bạn vào 4 chỗ ngồi là một hoán vị của 4 phần tử. Vì vậy số phần tử của không gian mẫu là 4! =24
b. Đánh số ghế theo thứ tự 1,2,3,4. Hai bạn nam ngồi cạnh nhau ở vị trí ( 1 và 2) hoặc (2 và 3) hoặc (3 và 4). Nếu hai bạn nam đổi chỗ cho nhau( giữ nguyên chỗ hai bạn nữ) thì Ta có một cách xếp mới. Vì vậy cần chọn phương án D
c. Trường hợp 1: bạn nam ngồi đầu.
Khi đó 2 bạn nam xếp vào 2 chỗ ( số ghế 1 và 3) có 2! cách, nữ xếp vào hai chỗ còn lại ( ghế số 2 và 4) có 2! cách
Suy ra: số cách xếp là 2!.2! = 4
Trường hợp 2: bạn nữ ngồi đầu. Tương tự có 4 cách xếp . Vậy theo quy tắc cộng số phần tử của biến cố N là 4+4=8
Bài 4: Gieo ngẫu nhiên ba đồng xu phân biệt một lần. Kí hiệu S, N lần lượt chỉ đồng xu lật sấp, lật ngửa
a) Hãy mô tả không gian mẫu
A. Ω={S,N,S}
B. Ω={SSS,SSN,SNS,NSS}
C. Ω={SSS,SSN,SNS,NSS,NNS,NSN,SNN,NNN}
D. Ω={NNN,NSN,SNS}
b) Xác định biến cố C:”có ít nhất hai đồng tiền xuất hiện mặt ngửa”
A. C={NNS,NSN,SNN}
B. C={NNS,NSN,SNN,NNN}
C. C={N,N,S}
D. C={N,N,N}
Lời giải:
a. Mỗi phần tử của không gian mẫu chỉ rõ ba đồng tiền xuất hiện ngẫu nhiên mặt sấp hay mặt ngửa.
Vì vậy cần chọn phương án C:
Ω = {SSS, SSN, SNS, NSS, NNS, NSN, SNN, NNN}
b. Biến cố C: “ Có ít nhất hai đồng tiền xuất hiện mặt ngửa” tức là có thể có hai hoặc ba đồng tiền xuất hiện mặt ngửa.
Vì vậy chọn phương án B: C = {NNS, NSN, SNN, NNN}.
Bài 5: Xét phép thử tung con súc sắc 6 mặt hai lần. Cho các biến cố:
A: “Số chấm xuất hiện ở cả hai lần tung giống nhau”
B: “ Tổng số chấm xuất hiện ở hai lần tung chia hết cho 3”
Tính |ΩA| + |ΩB|?
A. 18
B. 12
C. 16
D. 20
Lời giải:
* Ta có: Các kết quả thuận lợi để số chấm xuất hiện ở cả hai lần tung giống nhau là:
A = { (1, 1); (2, 2); (3,3); (4, 4); (5,5); (6, 6)}.
⇒ |ΩA| = 6
* Các kết quả thuận lợi để tổng số chấm xuất hiện ở hai lần tung chia hết cho 3 là:
B = { (1; 2); (2;1); (1; 5); (5; 1); (4; 2); (2; 4); (3; 3); (3; 6); (6;3); (4;5); (5; 4); (6; 6)}
⇒ |ΩB| = 12
⇒ |ΩA| + |ΩB| = 6 + 12 = 18
Bài 6: Bộ bài tú - lơ khơ có 52 quân bài. Rút ngẫu nhiên ra 4 quân bài. Tính xác suất của các biến cố A: “Rút ra được tứ quý K”.
Lời giải:
Bài 7: Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi. Tìm xác suất để 3 viên bi lấy ra đều màu đỏ.
Lời giải:
Bài 8. Gieo một con súc sắc cân đối, đồng chất và quan sát số chấm xuất hiện
a) Hãy mô tả không gian mẫu
A. Ω={2,4,6}
B. Ω={1,3,5}
C. Ω={1,2,3,4}
D. Ω={1,2,3,4,5,6}
b) Xác định biến cố A: ”Xuất hiện mặt có số chấm không nhỏ hơn 2”
A. A={1,2}
B. A={2,3}
C. A={2,3,4,5,6}
D. A={3,4,5,6}
Lời giải:
a) Quan sát con súc sắc có 6 mặt ghi số chấm 1,2,3,4,5,6. Vì vậy không gian mẫu Ω={1,2,3,4,5,6}. Chọn đáp án D
b) Biến cố A xảy ra khi mặt có số chấm không nhỏ hơn 2 xuất hiện
Vậy A={2, 3, 4, 5, 6}.
Chọn đáp án C
Bài 9. Gieo một con súc sắc sau đó gieo một đồng tiền. Quan sát số chấm xuất hiện trên con súc sắc và sự xuất hiện của mặt sấp (S), mặt ngửa (N) của đồng tiền.
a) Hãy mô tả không gian mẫu
A. Ω={1S,2N,3S,4N,5S,6N}
B. Ω={1N,2S,3N,4S,5N,6S}
C. Ω={1S,2,S,3S,4S,5S,6S,1N,2N,3N,4N,5N,6N}
D. Ω={SS,SN,NS}
b) Xác định biến cố M:”con súc sắc xuất hiện mặt chẵn chấm và đông tiền xuất hiện mặt sấp”
A. M={2S}
B. M={4S}
C. M={6S}
D. M={2S,4S,6S}
Lời giải:
a) Gieo con súc sắc độc lập với đồng tiền nên các khả năng có thể xảy ra là: Ω = {1S, 2S, 3S, 4S, 5S, 6S, 1N, 2N, 3N, 4N, 5N, 6N}
b) Biến cố M:”con súc sắc xuất hiện mặt chẵn chấm và đồng tiền xuất hiện mặt sấp” nên M = {2S, 4S, 6S}.
Chọn đáp án C
b) Chọn đáp án là D
Bài 10. Gieo một đồng xu cân đối và đồng chất liên tiếp cho đến khi lần đầu tiên xuất hiện mặt sấp hoặc cả năm lần ngửa thì dừng lại.
a. Mô tả không gian mẫu.
b. Xác định các biến cố:
A: “Số lần gieo không vượt quá ba”
B: “Có ít nhất 2 lần gieo xuất hiện mặt ngửa”
Lời giải:
Kí hiệu mặt sấp là S, mặt ngửa là N.
a. Ta có Ω = {S; NS; NNS; NNNS; NNNNS;" NNNNN" }⇒|Ω|=6.
b. A = {S; NS; NNS} ⇒ |ΩA| = 3.
B = {NNS; NNNS; NNNNS; NNNN} ⇒ |ΩB| = 4.
II. Bài tập tự luận có giải
Bài 1:Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của
1. Không gian mẫu
2. Các biến cố:
a) A: “ 4 viên bi lấy ra có đúng hai viên bi màu trắng”.
b) B : “ 4 viên bi lấy ra có ít nhất một viên bi màu đỏ”.
c) C: “ 4 viên bi lấy ra có đủ 3 màu”.
Lời giải:
1. Trong hộp có tất cả: 6 + 8 + 10 = 24 viên bi
Ta có, số phần tử của không gian mẫu chính là số cách lấy 4 viên bi từ 24 viên bi:
2. a) Số cách chọn 4 viên bi trong đó có đúng hai viên bị màu trắng, 2 viên bi còn lại màu đỏ hoặc xanh là: 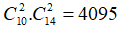
Suy ra |ΩA| = 4095.
b) Số cách lấy 4 viên bi mà không có viên bi màu đỏ được chọn là 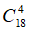
Suy ra số cách lấy 4 viên bi lấy ra có ít nhất một viên bi màu đỏ:
c)
Bài 2: Gieo hai đồng tiền một lần. Kí hiệu S,N để chỉ đông tiền lật sấp, lật ngửa
a) Mô tả không gian mẫu
b) Xác định biến cố M: “hai đồng tiền xuất hiện hai mặt không giống nhau”
Lời giải:
1.a. Gieo hai đồng tiền một lần.
Mô tả không gian mẫu: Ω = {SN, NS, SS, NN}
1.b. Biến cố M: “hai đồng tiền xuất hiện hai mặt không giống nhau” nên
M = {NS, SN}
Bài 3: Chọn ngẫu nhiên một số tự nhiên có 4 chữ số đôi một khác nhau. Tính số phần tử của
a. Không gian mẫu?
b. Biến cố A: “Số được chọn chia hết cho 5”
Lời giải:
Gọi 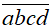
a. Số các số tự nhiên có bốn chữ số đôi một khác nhau là:
* có 9 cách chọn a.
* Sau khi chọn a, còn 9 số khác a nên có 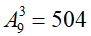
Suy ra |Ω| = 9.504 = 4536.
b) *TH1: nếu d = 5
Có 8 cách chọn a (a khác 0 và a khác d).
Với mỗi cách chọn a có, 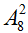
Có 8.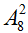
*TH2: Nếu d = 0, có 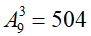
Nên có 504 số có 4 chữ số khác nhau chia hết cho 5 có chữ số hàng đơn vị là 0.
Vậy số có 4 chữ số khác nhau và chia hết cho 5 là: |Ω| = 448 + 504 = 952.
Bài 4: Từ các chữ số 1,2,3,4 ta lập các số tự nhiên có 3 chữ số khác nhau.
a) Tính số phần tử không gian mẫu
b) Phát biểu biến cố A={123,234,124,134} dưới dạng mệnh đề
Lời giải:
a. Gọi số tự nhiên có 3 chữ số khác nhau được tạo ra từ các số 1;2;3;4 là
Mỗi số tự nhiên có 3 chữ số thỏa mãn đầu bài là 1 chỉnh hợp chập 3 của 4 phần tử nên có 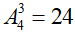
Vậy số phần tử của không gian mẫu là |Ω| = 24.
b. Phát biểu biến cố A = {123, 234, 124, 134} dưới dạng mệnh đề: Số tự nhiên có ba chữ số được thành lập từ các số 1; 2; 3; 4 có chữ số đứng sau lớn hơn chữ số đứng trước
Bài 5: Gieo một đồng tiền ba lần
a) Mô tả không gian mẫu.
b) Xác định các biến cố:
A: "Lần đầu xuất hiện mặt sấp"
B: "Mặt sấp xảy ra đúng một lần"
C: "Mặt ngửa xảy ra ít nhất một lần"
Lời giải:
a) Phép thử T được xét là: "Gieo một đồng tiền ba lần". Có thể liệt kê các phần tử của không gian mẫu của phép thử T nhờ sơ đồ cây sau đây:
Không gian (KG) mẫu:
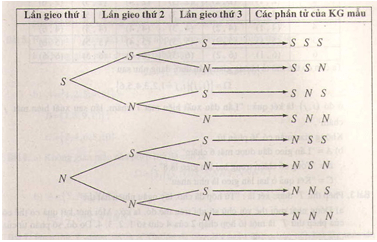
Do đó Ω = {SSS, SSN, SNS, SNN, NSS, NSN, NNS, NNN}.
b) A = {SSS, SSN, SNS, SNN}
B = {SNN, NSN, NNS}
C = {SSN, SNS, SNN, NSS, NSN, NNS, NNN} = Ω \ {SSS}.
Bài 6 Gieo một con súc sắc hai lần
a) Mô tả không gian mẫu.
b) Phát biểu các biến cố sau dưới dạng mệnh đề:
A = {(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
B = {(2, 6), (6, 2), (3, 5), (5, 3), (4, 4)}
C = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}.
Bài 7 Phép thử T được xét là: "Gieo một con súc sắc hai lần".
a) Các phần tử của không gian mẫu của phép thử T được liệt kê trong bảng sau đây.
Lời giải:
Trong bảng này, cột I là các mặt i chấm có thể xảy ra ở lần gieo thứ nhất, i = 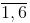
Dòng II (dòng trên cùng) là các mặt j chấm có thể xảy ra ở lần gieo thứ 2, j = 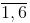
Mỗi ô (i, j) (giao của dòng i và cột j, 1 ≤ i, j ≤ 6) biểu thị một kết quả có thể có của phép thử T là: Lần gieo thứ nhất ra mặt i chấm, lần gieo thứ 2 ra mặt j chấm.
Không gian mẫu:

Ta còn có thể mô tả không gian mẫu dưới dạng như sau:
Ω = {(i, j) | i, j = 1, 2, 3, 4, 5, 6}
Ở đó (i, j) là kết quả: "Lần đầu xuất hiện mặt i chấm, lần sau xuất hiện mặt j chấm".
Không gian mẫu có 36 phần tử.
b) A = "Lần gieo đầu được mặt 6 chấm"
B = "Tổng số chấm trong hai lần gieo là 8"
C = "Kết quả ở hai lần gieo là như nhau"
Bài 8 Một hộp chứa bốn cái thẻ được đánh số 1, 2, 3, 4. Lấy ngẫu nhiên hai thẻ
a) Mô tả không gian mẫu.
b) Xác định các biến cố sau.
A: "Tổng các số trên hai thẻ là số chẵn"
B: "Tích các số trên hai thẻ là số chẵn"
Lời giải:
a. Mô tả không gian mẫu bằng cách liệt kê các phần tử của không gian mẫu.
b. A là tập con của không gian mẫu sao cho tổng các số trên hai thẻ là số chẵn.
B là tập con của không gian mẫu sao cho tích các số trên hai thẻ là số chẵn
Bài 9 Gieo một đồng tiền ba lần:
a) Mô tả không gian mẫu.
b) Xác định các biến cố
III. Bài tập vận dụng
Bài 1 Hai xạ thủ cùng bắn vào bia. Kí hiệu Ak là biến cố: "Người thứ k bắn trúng", k = 1, 2.
a) Hãy biểu diễn các biến cố sau qua các biến cố A1A2
A: "Không ai bắn trúng"
B: "Cả hai đểu bắn trúng"
C: "Có đúng một người bắn trúng"
D: "Có ít nhất một người bắn trúng"
b) Chứng tỏ rằng A = ![]() ; B và C xung khắc.
; B và C xung khắc.
Bài 2 Phép thử T được xét là: "Hai xạ thủ cùng bắn vào bia".
Theo đề ra ta có ![]() = "Người thứ k không bắn trúng", k = 1, 2.
= "Người thứ k không bắn trúng", k = 1, 2.
a) A = "Không ai bắn trúng" = "Người thứ nhất không bắn trúng và người thứ hai không bắn trúng". Suy ra A = ![]() .
.![]()
b) Tương tự, ta có B = "Cả hai đều bắn trúng" = ![]() .
.![]()
Bài 3 Từ một hộp chứa 10 cái thẻ, trong đó các thẻ đánh số 1, 2, 3, 4, 5 màu đỏ, thẻ đánh số 6 màu xanh và các thẻ đánh số 7, 8, 9, 10 màu trắng. Lấy ngẫu nhiên một thẻ.
a) Mô tả không gian mẫu.
b) Kí hiệu A, B, C là các biến cố sau:
A: "Lấy được thẻ màu đỏ"
B: "Lấy được thẻ màu trắng"
C: "Lấy được thẻ ghi số chẵn"
Bài 4 Hãy biểu diễn các biến cố A, B, C bởi các tập hợp con tương ứng của không gian mẫu.
Bài 5 Gieo một đồng tiền liên tiếp cho đến khi lần đầu tiên xuất hiện mặt sấp hoặc cả bốn lần ngửa thì dừng lại.
a) Mô tả không gian mẫu.
b) Xác định các biến cố
Bài 6 Từ một hộp chứa năm quả cầu được đánh số 1, 2, 3, 4, 5, lấy ngẫu nhiên liên tiếp hai lần mỗi lần một quả và xếp theo thứ tự từ trái sang phải.
a) Mô tả không gian mẫu.
b) Xác định các biến cố sau:
A: "Chữ số sau lớn hơn chữ số trước"
B: "Chữ số trước gấp đôi chữ số sau"
C: "Hai chữ số bằng nhau".
Bài 7 Gieo một đồng tiền ba lần:
a) Mô tả không gian mẫu.
b) Xác định các biến cố:
A: "Lần đầu xuất hiện mặt sấp";
B: "Mặt sấp xảy ra đúng một lần";
C: "Mặt ngửa xảy ra ít nhất một lần".
Bài 8 Gieo một con súc sắc hai lần.
a) Mô tả không gian mẫu.
b) Phát biểu các biến cố sau dười dạng mệnh đề:
A = {(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)};
B = {(2, 6), (6, 2), (3, 5), (5, 3), (4, 4)};
C = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}.
Bài 9 Hai xạ thủ cùng bắn vào bia.Kí hiệu Ak là biến cố: "Người thứ k bắn trúng", k = 1, 2.
a) Hãy biểu diễn các biến cố sau qua các biến cố A1 A2 :
A: "Không ai bắn trúng";
B: "Cả hai đểu bắn trúng";
C: "Có đúng một người bắn trúng";
D: "Có ít nhất một người bắn trúng".
Bài 10
a) Mô tả không gian mẫu.
b) Kí hiệu A, B, C là các biến cố sau:
A: "Lấy được thẻ màu đỏ";
B: "Lấy được thẻ màu trằng";
C: "Lấy được thẻ ghi số chẵn".
Hãy biểu diễn các biến cố A, B, C bởi các tập hợp con tương ứng của không gian mẫu.