85 Bài tập về nhị thức Niu-tơn (có đáp án năm 2023) - Toán 11

Bài giảng Toán 11 Bài 3: Nhị thức Niu-tơn

Kiến thức cần nhớ

I. Công thức nhị thức Niu- tơn

Ta có:

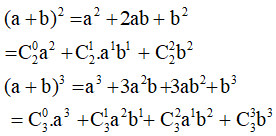
- Công thức nhị thức Niu – tơn.

$$\begin{gathered} {(a\text{\hspace{0.17em}\hspace{0.17em}}+b)}^n=C_n^0{a}^n+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^1.a^{n-1}b \\ +\text{\hspace{0.17em}}\mathrm{...}+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^k.a^{n-k}{b}^k\text{\hspace{0.17em}}+\text{}\mathrm{....}+ \\ \text{}{C}_n^{n-1}a{b}^{n-1}+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^n{b}^n \end{gathered}$$

- Hệ quả:

Với a = b = 1 ta có: $2^n=C_n^0+\text{\hspace{0.17em}}{C}_n^1+\text{}\mathrm{...}\text{}+\text{\hspace{0.17em}}{C}_n^n$

Với a = 1; b = – 1 ta có: $0=C_n^0-\text{\hspace{0.17em}}{C}_n^1+\text{}\mathrm{...}$$+\text{}{(-1)}^k.C_n^k+\text{}\mathrm{...}\text{}+{(-1)}^n\text{\hspace{0.17em}}{C}_n^n$

- Chú ý:

Trong biểu thức ở vế phải của công thức (1):

a) Số các hạng tử là n + 1.

b) Các hạng tử có số mũ của a giảm dần từ n đến 0; số mũ của b tăng dần từ 0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n (quy ước $a^0=b^0=1$).

c) Các hệ số của mỗi cặp hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.

- Ví dụ 1. Khai triển biểu thức: (a – b)⁵.

Lời giải:

Áp dụng công thức nhị thức Niu – tơn ta có:

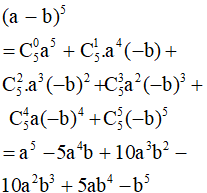
- Ví dụ 2. Khai triển biểu thức: (3x – 2)⁴.

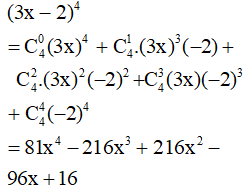
II. Tam giác Pa- xcan

Trong công thức nhị thức Niu – tơn ở mục I, cho n = 0; 1; … và xếp các hệ số thành dòng, ta nhận được tam giác sau đây, gọi là tam giác Pa- xcan.

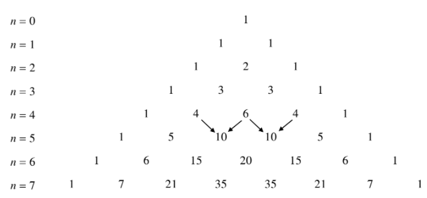
- Nhận xét:

Từ công thức $C_n^k=C_{n-1}^{k-1}+C_{n-1}^k$ suy ra cách tính các số ở mỗi dòng dựa vào các số ở dòng trước nó.

Ví dụ 3. $C_6^2=C_5^1+C_5^2=5+10=15$.

Các dạng bài toán về nhị thức Niu-tơn

Dạng 1. Tìm hệ số, số hạng trong khai triển không có điều kiện.

+ Bước 1: Viết khai triển dạng tổng quát.

+ Bước 2: Dựa vào giả thiết yêu cầu tìm hệ số của m x giải phương trình m f k k.

+ Bước 3: Thay vào biểu thức của T và kết luận.

Dạng 2. Tìm hệ số, số hạng trong khai triển có điều kiện.

+ Bước 1: Tìm n dựa vào điều kiện đề bài cho.

+ Bước 2: Quy về dạng 1 đã biết.

Dạng 3. Tìm hệ số, số hạng trong khai triển nhiều hạng tử.

+ Bước 1: Viết khai triển thu gọn về 2 hạng tử.

+ Bước 2: Dựa vào chỉ số mũ của x để biện luận tìm i và k.

+ Bước 3: Kết luận về hệ số của số hạng cần tìm.

Bài tập tự luyện

1. Bài tập vận dụng

Bài 1. Viết khai triển theo công thức nhị thức Niu- tơn.

a) (2x – 1)⁶.

b) (2x + 2y)⁵.

Lời giải:

Theo khai triển nhị thức Niu- tơn ta có:

a)

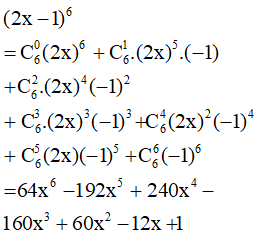
b)

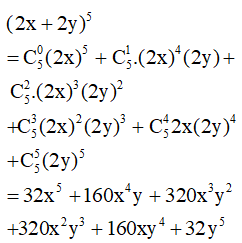
Bài 2. Tìm hệ số chứa x⁴ trong khai triển biểu thức ${\left(x-\frac{1}{x}\right)}^{10}$.

Lời giải:

Số hạng thứ k + 1 trong khai triển là:

$\begin{array}{l}{T}_{k+\text{}1}=C_{10}^k.x^{10-k}.{\left(\frac{-1}{x}\right)}^k\\ =C_{10}^k.{\left(-1\right)}^k.x^{10-2k}\end{array}$

Để số hạng này chứa x⁴ thì điều kiện là:

10 – 2k = 4 nên k = 3.

Vậy hệ số chứa x⁴ trong khai triển đã cho là: $C_{10}^3.{(-1)}^3=-120$.

Bài 3. Tìm số hạng thứ 8 trong khai triển (2x + 3y)¹²

Lời giải:

Số hạng thứ k + 1 trong khai triển là: 

$$\begin{gathered} T_{k+\text{}1}=C_{12}^k.{\left(2x\right)}^{12-k}.{\left(3y\right)}^k \\ =C_{12}^k.2^{12-k}{.3}^k.{\left(x\right)}^{12-k}.y^k \end{gathered}$$

Suy ra, số hạng thứ 8 trong khai triển ứng với k + 1 = 8 nên k = 7.

Vậy số hạng thứ 8 trong khai triển là:

$$\begin{gathered} T_8=C_{12}^7{.2}^5{.3}^7.x^5.y^7 \\ =55427328x^5.y^7 \end{gathered}$$

Bài 4. Biết hệ số của x³ trong khai triển của (2 – 4x)ⁿ là –10 240.  Tìm n.

Lời giải:

Số hạng thứ k + 1 trong khai triển là:

$$\begin{gathered} T_{k+1}=C_n^k{.2}^{n-k}.{(-4x)}^k \\ =C_n^k{.2}^{n-k}.{(-4)}^k{x}^k \end{gathered}$$

Để số hạng này chứa x³ thì k = 3.

2. Bài tập tự luyện có hướng dẫn