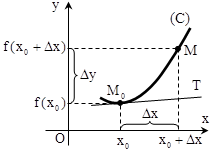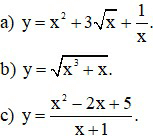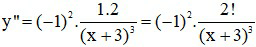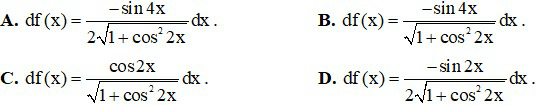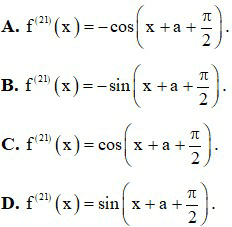20 Bài toán về vi phân, đạo hàm cấp cao và ý nghĩa của đạo hàm (2024) hay, chi tiết, có đáp án

Các bài toán về vi phân, đạo hàm cấp cao và ý nghĩa của đạo hàm

Lý thuyết

1. Vi phân

- Cho hàm số y = f(x) xác định trên (a ; b) và có đạo hàm tại x ∈ (a;b). Giả sử ∆x là số gia của x sao cho x + ∆x ∈ (a;b).

- Tích f'(x).∆x (hay y.∆x) được gọi là vi phân của hàm số y = f(x) tại x, ứng với số gia ∆x, kí hiệu là df(x) hay dy.

Vậy ta có: dy = y'.∆x hoặc df(x) = f'(x).∆x.

2. Đạo hàm cấp cao

Cho hàm số y = f(x) có đạo hàm f’(x). Hàm số f’(x) còn gọi là đạo hàm cấp 1 của hàm số f(x). Nếu hàm số f’(x) có đạo hàm thì đạo hàm đó được gọi là đạo hàm cấp 2 của hàm số f(x), kí hiệu là y’’ hay f’’(x). Đạo hàm của đạo hàm cấp 2 được gọi là đạo hàm cấp 3 của hàm số f(x), kí hiệu là y’’’ hay f’’’(x). Tương tự, ta gọi đạo hàm của đạo hàm cấp (n – 1) là đạo hàm cấp (n) của hàm số f(x), kí hiệu là y⁽ⁿ⁾ hay f⁽ⁿ⁾(x), tức là ta có: 

y⁽ⁿ⁾ = (y⁽ⁿ⁻¹⁾)' (n ∈ N, n > 1).

3. Ý nghĩa của đạo hàm

- Ý nghĩa hình học

+ Tiếp tuyến của đường cong phẳng: 

Cho đường cong phẳng (C) và một điểm cố định M₀ trên (C), M là điểm di động trên (C). Khi đó M₀ M là một cát tuyến của (C).

Định nghĩa: Nếu cát tuyến M₀ M có vị trí giới hạn M₀T khi điểm M di chuyển trên (C) và dần tới điểm M₀ thì đường thẳng M₀T được gọi là tiếp tuyến của đường cong (C) tại điểm M₀ . Điểm M₀ được gọi là tiếp điểm.

+ Ý nghĩa hình học của đạo hàm:

Cho hàm số y = f(x) xác định trên khoảng (a; b) và có đạo hàm tại x₀ ∈ (a;b), gọi (C) là đồ thị hàm số đó.

Định lí 1: Đạo hàm của hàm số f(x) tại điểm x₀ là hệ số góc của tiếp tuyến M₀T của (C) tại điểm M₀ (x₀; f(x₀)) 

Phương trình tiếp tuyến:

Định lí 2: Phương trình tiếp tuyến của đồ thị (C) của hàm số y = f(x) tại điểm M₀ (x₀; f(x₀)) là: y = f’(x₀).(x – x₀) + f(x₀)

- Ý nghĩa vật lí

Vận tốc tức thời: Xét chuyển động thẳng xác định bởi phương trình: s = f(t), với f(t) là hàm số có đạo hàm. Khi đó, vận tốc tức thời của chất điểm tại thời điểm t₀ là đạo hàm của hàm số s = f(t) tại t₀ .

v(t₀) = s’(t₀) = f’(t₀)

Cường độ tức thời: Điện lượng Q truyền trong dây dẫn xác định bởi phương trình: Q = f(t), với f(t) là hàm số có đạo hàm. Khi đó, cường độ tức thời của dòng điện tại thời điểm t₀ là đạo hàm của hàm số Q = f(t) tại t₀ .

I(t₀) = Q’(t₀) = f’(t₀) 

4. Ý nghĩa cơ học của đạo hàm cấp hai

Xét chuyển động thẳng xác định bởi phương trình: s = f(t) với f(t) là hàm số có đạo hàm.

Khi đó, gia tốc tức thời a của chuyển động tại thời điểm t là đạo hàm cấp hai của hàm số
 s = f(t) tại t là a(t) = f’’(t) .

Các dạng bài tập

Dạng 1: Tìm vi phân của hàm số

Phương pháp giải:

Áp dụng định nghĩa để tìm vi phân của hàm số y = f(x) là: dy = f’(x)dx

Ví dụ minh họa:

Ví dụ 1: Tìm vi phân của hàm số 

Lời giải

a)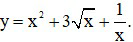  

Ta có: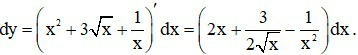  

b)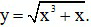  

Ta có :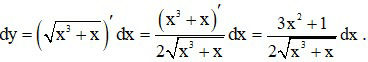  

c)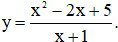  

Ta có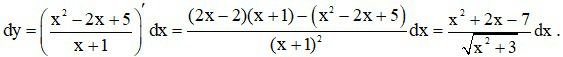  

Ví dụ 2: Tìm vi phân của hàm số

a) y = cos 3x.sin 2x.

b) y = f(x) = sin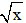 + cos

Lời giải

a) y = cos 3x.sin 2x.

y’ = (cos 3x)’sin 2x + cos 3x(sin 2x)’ 

= – 3sin 3x.sin 2x + 2cos 3x.cos 2x

Suy ra dy = (– 3sin3x.sin2x + 2 cos3x.cos2x)dx

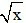
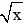
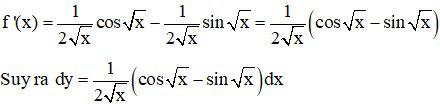
b) y = f(x) = sin + cos 

Dạng 2: Tính đạo hàm cấp cao của hàm số

Phương pháp giải: 

Tính đạo hàm cấp 2 là đạo hàm của đạo hàm cấp 1

Tính đạo hàm cấp 3 là đạo hàm của đạo hàm cấp 2

Tương tự: Tính đạo hàm cấp n là đạo hàm của đạo hàm cấp n – 1.

Ví dụ minh họa:

Ví dụ 1: Tính đạo hàm đến cấp đã chỉ ra:

a) y = xsin 2x, (y’’’) 

b) y = cos² x,  (y’’’)

c)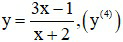  

Lời giải

a) y = xsin2x, (y’’’) 

Ta có y’ = x’sin 2x + x .(sin 2x)’ = sin 2x + 2xcos 2x

y’’ = (sin 2x)’ + (2x)’cos 2x + 2x(cos 2x)’ = 4cos2x – 4xsin 2x 

y’’’ = 4(cos 2x)’ – (4x)sin 2x – 4x(sin 2x)’ 

= – 8sin 2x – 4sin 2x – 8cos 2x

= – 12sin 2x – 8cos 2x 

b) y = cos²x,  (y’’’)

Ta có: y = cos²x = ½(1 + cos2x)

y’ = – sin 2x

y’’ = – 2cos 2x

y’’’ = 4sin 2x

c)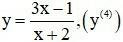  

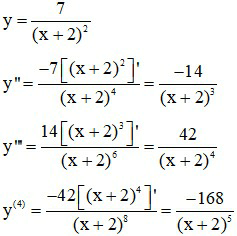
Ví dụ 2: Tính đạo hàm cấp n của hàm số

a) y = x⁴ + 4 x³ – 3x² + 1

b)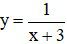  

Lời giải

a) y = x⁴ + 4 x³ – 3x² + 1

y’ = 4x³ + 12 x² – 6x 

y’’ = 12x² + 24x – 6 

y’’’ = 24 x + 24

y⁽⁴⁾ = 24 

Suy ra y⁽⁵⁾ = 0, … y⁽ⁿ⁾ = 0.

b)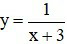  

Ta có: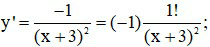  

Dự đoán: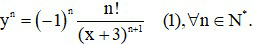  

Chứng minh (1) bằng phương pháp quy nạp:

* n = 1: (1) hiển nhiên đúng.

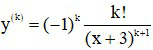
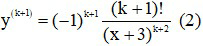
* Giả sử (1) đúng với n = k ≥ 1, nghĩa là ta có:  ta phải chứng minh (1) cũng đúng với n = k + 1, nghĩa là ta phải chứng minh:  

Thật vậy:

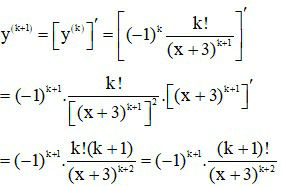
Vậy (2) đúng nghĩa là (1) đúng với n = k + 1.

Theo nguyên lí quy nạp ta suy ra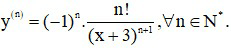  

Dạng 3: Ý nghĩa cơ học của đạo hàm cấp 2

Phương pháp giải:

Xét chuyển động thẳng xác định bởi phương trình: s = f(t) với f(t) là hàm số có đạo hàm.

Để tính gia tốc tức thời a của chuyển động tại thời điểm t là đạo hàm cấp hai của hàm số
 s = f(t) tại t:

- Đạo hàm f(t) đến cấp 2

- Gia tốc a(t) = f’’(t)

Ví dụ minh họa:

Ví dụ 1. Một chất điểm chuyển động thẳng được xác định bởi phương trình: s = t³ – 3t² + 5t + 2, trong đó t tính bằng giây và s tính bằng mét. Tính gia tốc của chuyển động khi t = 3.

Lời giải

Gia tốc chuyển động tại t = 3s là s"(3)

Ta có: s’(t) = 3t² – 6t + 5

s’’(t) = 6t – 6

Vậy s’’(3) = 6.3 – 6 = 12 m/s². 

Ví dụ 2. Một chất điểm chuyển động thẳng xác định bởi phương trình s = t³ – 2t² + 4t + 1 trong đó t là giây, s là mét. Tính gia tốc của chuyển động khi t = 2 là:

Lời giải

Gia tốc chuyển động tại t = 2s là s"(2)

Ta có: s’(t) = 3t² – 6t + 4

s’’(t) = 6t – 6

Vậy s’’(2) = 6.2 – 6 = 6 m/s².

Dạng 4. Ý nghĩa vật lý của đạo hàm của đạo hàm 

Phương pháp giải:

Lưu ý hai kết quả sau để áp dụng:

-  Vận tốc tức thời tại thời điểm t₀ của chất điểm chuyển động với phương trình s = s(t) là v(t₀) = s’(t₀).

- Cường độ tức thời tại thời điểm t₀ của một dòng điện với điện lượng Q = Q(t) là I(t₀) = Q’(t₀).

Ví dụ minh họa:

Ví dụ 1: Một chất điểm chuyển động có phương trình chuyển động là: s = f(t) = t² + 4t + 6 (t được tính bằng giây, s được tính bằng mét)

a) Tính đạo hàm của hàm số f(t) tại điểm t₀ .

b) Tính vận tốc tức thời của chuyển động tại thời điểm t = 5.

Lời giải

a) Ta có: f’(t) = 2t + 4.

Vậy f’(t₀) = 2t_­0 + 4.

b) Vận tốc tức thời của chuyển động tại thời điểm t = 5 là v = f’(5) = 2.5 + 4 = 14 (m/s).

Ví dụ 2: Cho biết điện lượng trong một dây dẫn theo thời gian biểu thị bởi hàm số Q = 6t + 5 (t được tính bằng giây, Q được tính bằng Coulomb). Tính cường độ của dòng điện trong dây dẫn tại thời điểm t = 10.

Lời giải

Vì Q’(t) = 6 nên cường độ của dòng điện trong dây dẫn tại thời điểm t = 10 là I  = Q’(10) = 6.

Bài tập tự luyện (có đáp án)

Câu 1. Cho hàm số y = f(x) = (x – 1)² . Biểu thức nào sau đây chỉ vi phân của hàm số f(x)?

A. dy = 2(x – 1) dx                                  B. dy = (x – 1)²dx     

C. dy = 2(x – 1)                                       D. dy = 2(x – 1) dx.

Câu 2. Xét hàm số 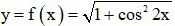. Chọn câu đúng:

Câu 3. Cho hàm số 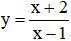 . Vi phân của hàm số là:

Câu 4. Cho hàm số f(x) = x³ + 2x, giá trị của f’’(1) bằng

A. 6.                      B. 8.                          C. 3.                          D. 2.

Câu 5. Cho hàm số 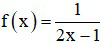 . Tính f’’(– 1).

Câu 6. Cho hàm số f(x) = cos2x. Tính P = f''(π).

A. P = 4.                B. P = 0.                    C. P = – 4.                D. P = – 1.

Câu 7. Cho hàm số: 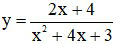. Phương trình y’’ = 0 có nghiệm là:

A. x = -4.               B. x = – 2.                 C. x = 0.                    D. x = 2.

Câu 8. Cho hàm số y = sin 2x. Khẳng định nào sau đây là đúng?

A. y² – (y’)² = 4.                                      B. 4y + y’’ = 0.         

C. 4y – y’’ = 0.                                        D. y = y’.tan 2x.

Câu 9. Cho hàm số y = sin²x. Khẳng định nào sau đây đúng?

A.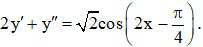                    

B. 2y + y’. tan x = 0.

C. 4y- y’’ = 2.                                         

D. 4 y’ + y’’’ = 0.

Câu 10. Cho hàm số 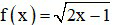. Tính f’’’(1).

A. 3.                      B. -3.                         C. 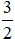                         D. 0.

Câu 11. Đạo hàm cấp 21 của hàm số f(x) = cos (x + a) là

Câu 12. Một chất điểm chuyển động có phương trình chuyển động là: s = f(t) = t² + t + 6 (t được tính bằng giây, s được tính bằng mét). Vận tốc tức thời của chuyển động tại thời điểm t = 2 là

A. 5 (m/s).             B. 6 (m/s).                 C. 7 (m/s).                 D. 4 (m/s).

Câu 13. Cho chuyển động thẳng xác định bởi phương trình 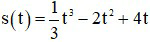 trong đó t được tính bằng giây và s được tính bằng mét. Sau bao lâu thì chuyển động dừng lại?

A. 1 (s).                 B. 3 (s).                     C. 2 (s).                     D. 4 (s).

Câu 14. Cho biết điện lượng trong một dây dẫn theo thời gian biểu thị bởi hàm số Q = 3t² + 6t + 5 (t được tính bằng giây, Q được tính bằng Coulomb). Tính cường độ của dòng điện trong dây dẫn tại thời điểm t = 1.

A. 5 (A).                B. 12 (A).                  C. 7 (A).                    D. 4 (A).

Câu 15. Một vật chuyển động theo quy luật 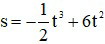 với t (giây)là khoảng thời gian từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển trong thời gian đó. Hỏi trong khoảng thời gian 6 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất vật đạt được bằng bao nhiêu?

A. 24 (m/s).           B. 108 (m/s).             C. 64 (m/s).               D. 18 (m/s).

Bảng đáp án