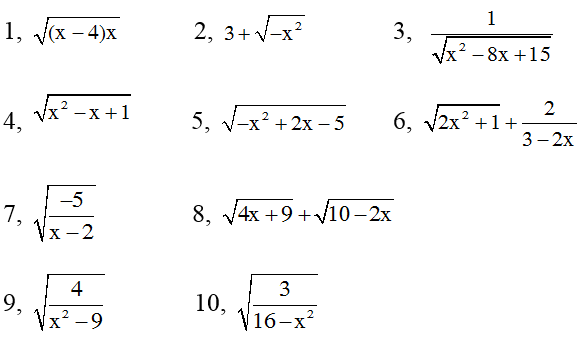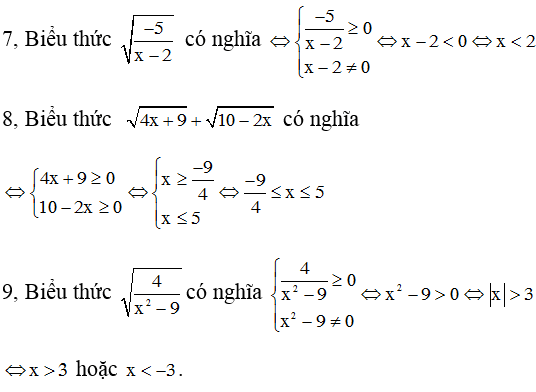Tìm điều kiện để biểu thức căn có nghĩa
Phương pháp giải
+) xác định (hay có nghĩa) khi .
+) Các tính chất của bất đẳng thức:
1) , nếu .
2) , nếu .
3) , với mọi .
+) Điều kiện để phân thức có nghĩa là mẫu thức khác 0.
Ví dụ minh họa
Ví dụ 1:Tìm x để biểu thức có nghĩa
Lời giải:
có nghĩa khi 5 - 2x ≥ 0 ⇔ 5 ≥ 2x ⇔ x ≤ 5/2
Vậy với x ≤ 5/2 thì biểu thức đã cho có nghĩa.
Ví dụ 2: Tìm x để biểu thức có nghĩa?
Lời giải:
Bài tập vận dụng (có đáp án)
Bài 1: Tìm x để các biểu thức sau có nghĩa
Hướng dẫn giải
Bài 2: Tìm x để mỗi căn thức sau có nghĩa:
a); c)
b) d)
Hướng dẫn giải:
a) Ta có:
có nghĩa khi và chỉ khi:
.
b) Ta có
có nghĩa khi và chỉ khi:
c) Ta có:
có nghĩa khi và chỉ khi:
d)
Ta có: , với mọi số thực
, (Cộng cả 2 vế của bất đẳng thức trên với )
, mà
Vậy căn thức trên luôn có nghĩa với mọi số thực .
Bài 3: Tìm x để căn thức sau có nghĩa:
a)
b)
c)
d)
Hướng dẫn giải
a) Ta có: có nghĩa khi:
-2x + 3 0
Vậy thì căn đã cho có nghĩa
b) Ta có: có nghĩa khi
Vì 2 > 0 và với mọi x nên
khi
Vậy thì căn đã cho có nghĩa
c) Ta có: có nghĩa khi
Vì 4 > 0 nên để thì
Vậy thì căn đã cho có nghĩa
d) Ta có: ≥ 0 với mọi x
nên + 6 > 0 với mọi x
Mà -5 < 0
< 0 với mọi x
Do đó không tồn tại giá trị nào của x để
Vậy không có giá trị nào của x để căn thức đã cho có nghĩa.
Bài 4: Tìm x để mỗi căn thức sau có nghĩa:
a); c)
b) d)
Hướng dẫn giải:
a)
có nghĩa khi và chỉ khi:
b)
có nghĩa khi và chỉ khi:
c)
có nghĩa khi và chỉ khi
mà tức là
d)
Vì với mọi số thực x nên .
Vậy căn thức trên luôn có nghĩa
Xem thêm các dạng Toán lớp 9 đầy đủ, chi tiết và hay khác:
50 Bài tập Căn thức bậc hai và hằng đẳng thức √ A 2 = | A | (có đáp án năm 2023) - Toán 9
50 Bài tập Biến đổi đơn giản biểu thức căn thức bậc hai (có đáp án năm 2023) - Toán 9
50 Bài tập Rút gọn biểu thức chứa căn thức bậc hai (có đáp án năm 2023) - Toán 9