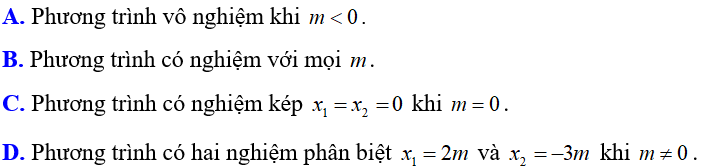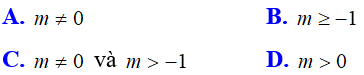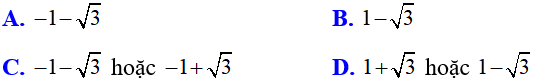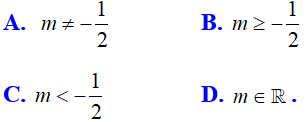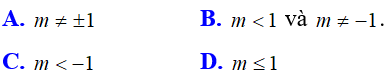Cách giải và biện luận phương trình bậc hai theo tham số m
1. Phương pháp giải
Giải phương trình: ax2 + bx + c = 0, trong đó a, b, c là các biểu thức phụ thuộc vào m.
Bước 1: Xác định các hệ số a, b, c (hoặc a, b', c ).
Bước 2: Giải phương trình theo m:
+) Với giá trị của m mà a = 0, giải phương trình bậc nhất.
+) Với giá trị của m mà a ≠ 0, giải phương trình bậc hai: Tính Δ = b2 - 4ac (hoặc Δ' = b'2 - 4ac), xét các trường hợp của Δ chứa tham số và tìm nghiệm theo tham số.
Bước 3: Kết luận.
Biện luận phương trình:
- Phương trình có nghiệm khi:
+) Với giá trị của m mà a = 0, phương trình bậc nhất có nghiệm.
+) Với giá trị của m mà a ≠ 0, phương trình bậc hai có nghiệm.
- Phương trình có một nghiệm khi:
+) Với giá trị của m mà a = 0, phương trình bậc nhất có nghiệm.
+) Với giá trị của m mà a ≠ 0, phương trình bậc hai có nghiệm kép.
- Phương trình có hai nghiệm phân biệt khi: Giá trị của m mà a ≠ 0, phương trình bậc hai có hai nghiệm phân biệt.
2. Các ví dụ điển hình
Ví dụ 1: Cho phương trình x2 + mx - 6m2 = 0 với m là tham số. Chọn khẳng định sai:
Lời giải
Chọn A
Ví dụ 2: Cho phương trình mx2 - 2(m + 1)x + m + 2 = 0. Chọn kết luận đúng.
Lời giải
Chọn B
Ví dụ 3: Khi phương trình x2 + (m + 1)x - m = 0 có nghiệm kép, giá trị của nghiệm kép là:
Lời giải
Chọn C
3. Bài tập vận dụng (có đáp án)
Bài 1: Phương trình mx2 + 2(m + 1)x + m + 1 = 0 (m là tham số) có nghiệm khi nào?
Lời giải:
Đáp án B
Bài 2: Tìm nghiệm của phương trình 2x2 - (m + 4)x - m = 0 khi phương trình có nghiệm kép.
Lời giải:
Đáp án C
Bài 3: Tìm giá trị lớn nhất của tham số m để phương trình x2 - 12x + m = 0 có nghiệm. Nghiệm của phương trình khi đó là:
Lời giải:
Đáp án D
Bài 4: Phương trình (2m + 1)x2 + (4m2 - 1)x - 4m2 - 2m = 0 có nghiệm khi:
Lời giải:
Đáp án D
Bài 5: Có bao nhiêu giá trị nguyên của tham số m, -10 ≤ m ≤ 10 để phương trình mx2 - mx + 1 = 0 có nghiệm ?
Lời giải:
Đáp án D
Bài 6: Số các giá trị nguyên âm của tham số m để phương trình x2 - 4x - m = 0 không nhận x = 2 - √5 làm nghiệm là:
Lời giải:
Đáp án A
Bài 7: Số các giá trị nguyên không âm của tham số m để phương trình x2 - (2m + 1)x + m2 + 2 = 0 vô nghiệm.
Lời giải:
Đáp án B
Bài 8: Tập nghiệm của phương trình mx2 + 4(m - 1)x + 4(m - 3) = 0 có một phần tử khi:
Lời giải:
Đáp án B
Bài 9: Cho phương trình 4x2 + 2(2m + 1)x + m2 = 0. Chọn khẳng định đúng.
Lời giải:
Đáp án A
Bài 10: Tìm m để phương trình (m2 - 1)x2 + 2(m + 1)x + 1 = 0 vô nghiệm.
Lời giải:
Đáp án D
Xem thêm các dạng bài tập Toán chi tiết và hay khác:
50 Bài tập Giải hệ phương trình bằng phương pháp thế (có đáp án năm 2023)
50 Bài tập Giải hệ phương trình bằng phương pháp cộng đại số (có đáp án năm 2023)
50 Bài tập Phương trình bậc hai một ẩn (có đáp án năm 2023)