Phương pháp đặt ẩn và giải hệ bất phương trình (2024) chi tiết nhất

Để giải hệ bất phương trình bậc nhất hai ẩn từ một bài tập cụ thể, ta cần xác định các bước sau đây:
Bước 1: Xác định công thức tổng quát của hệ bất phương trình.
- Đầu tiên, viết công thức của hệ bất phương trình bậc nhất hai ẩn theo dạng ax + by ≥ c và dx + ey ≥ f, với a, b, c, d, e, f là các hệ số cụ thể.
Bước 2: Đặt biến và xác định miền nghiệm.
- Đặt biến x và y để tìm miền nghiệm của hệ bất phương trình.
- Dựa trên điều kiện ràng buộc của hệ bất phương trình, xác định miền nghiệm của biến x và y. Miền nghiệm có thể là một tập hợp các giá trị hoặc một khoảng giới hạn của biến.
Bước 3: Giải hệ và xác định nghiệm.
- Giải hệ bất phương trình bậc nhất hai ẩn bằng cách tìm giá trị của x và y thỏa mãn cả hai bất phương trình.
- Xác định nghiệm của hệ bất phương trình, có thể là một tập hợp các cặp giá trị (x, y) thỏa mãn hay một cặp giá trị cụ thể.
Bước 4: Kiểm tra nghiệm.
- Kiểm tra nghiệm bằng cách thay giá trị của x và y vào từng bất phương trình ban đầu để xác minh xem chúng có thoả mãn hay không.
Lưu ý: Khi giải hệ bất phương trình bậc nhất hai ẩn, cần chú ý đến các trường hợp đặc biệt như hệ vô nghiệm, hệ có miền nghiệm rỗng hoặc hệ có vô số nghiệm.

II. Bài tập vận dụng 

Câu 1. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn ?

A.$\left\{\begin{array}{l}x+3y\ge 0\\ 2x\le 0\end{array}\right.$

B.$\left\{\begin{array}{l}{x}^2+3y\ge 2\\ 2x+y\le -1\end{array}\right.$

C.$\left\{\begin{array}{l}4x+3y-1\ge 0\\ x+y^3>0\end{array}\right.$

D. $\left\{\begin{array}{l}-x^2+3y\ge 5\\ x+y^3\le 1\end{array}\right.$

Đáp án đúng là: A

Các hệ bất phương trình  $\left\{\begin{array}{l}{x}^2+3y\ge 2\\ 2x+y\le -1\end{array}\right.$; $\left\{\begin{array}{l}4x+3y-1\ge 0\\ x+y^3>0\end{array}\right.$ ; $\left\{\begin{array}{l}-x^2+3y\ge 5\\ x+y^3\le 1\end{array}\right.$  đều chứa các bất phương trình bậc hai hoặc bậc ba như : x² + 3y ≥ 2 ; x + y³ > 0 ; – x² + 3y ≥ 5.

Do đó, các hệ bất phương trình  $\left\{\begin{array}{l}{x}^2+3y\ge 2\\ 2x+y\le -1\end{array}\right.$; $\left\{\begin{array}{l}4x+3y-1\ge 0\\ x+y^3>0\end{array}\right.$ ;  $\left\{\begin{array}{l}-x^2+3y\ge 5\\ x+y^3\le 1\end{array}\right.$ không phải là hệ bất phương trình bậc nhất hai ẩn.

Hệ $\left\{\begin{array}{l}x+3y\ge 0\\ 2x\le 0\end{array}\right.$ có hai bất phương trình x + 3y ≥ 0 và 2x ≤ 0 đều là các bất phương trình bậc nhất hai ẩn.

Vậy ta chọn đáp án A.

Câu 2. Trong các khẳng định sau, khẳng định nào đúng?

A. Điểm O(0 ; 0) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+3y\ge 0\\ 2x\le 0\end{array}\right.$

B. Điểm M(1 ; 0) thuộc miền nghiệm của hệ bất phương trình  $\left\{\begin{array}{l}-x+3y\ge 0\\ 2x\le 0\end{array}\right.$

C. Điểm N(0 ; –1) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+3y\ge 0\\ 2x\le 0\end{array}\right.$

D. Điểm P(1 ; 1) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+3y\ge 0\\ 2x\le 0\end{array}\right.$

Đáp án đúng là: A

+ Vì –0 + 3.0 = 0 và 2.0 = 0 nên cặp số (0; 0) là nghiệm của cả hai bất phương trình –x + 3y ≥ 0 và 2x ≤ 0.

Suy ra điểm O(0; 0) thuộc miền nghiệm của hệ $\left\{\begin{array}{l}-x+3y\ge 0\\ 2x\le 0\end{array}\right.$.

Vậy khẳng định A là đúng.

+ Vì –1 + 3.0 = –1 < 0 và 2. (–1)  = –2 < 0 nên cặp số (1 ; 0) không là nghiệm của bất phương trình –x + 3y ≥ 0.

Suy ra điểm M(1 ; 0) không thuộc miền nghiệm của hệ $\left\{\begin{array}{l}-x+3y\ge 0\\ 2x\le 0\end{array}\right.$.

Vậy khẳng định B là sai.

+ Vì –0 + 3. (–1) = –3 < 0 và 2. 0  = 0 nên cặp số (0; –1) không là nghiệm của bất phương trình –x + 3y ≥ 0.

Suy ra điểm N(0 ; –1) không thuộc miền nghiệm của hệ $\left\{\begin{array}{l}-x+3y\ge 0\\ 2x\le 0\end{array}\right.$.

Vậy khẳng định C là sai.

+ Vì –1 + 3. 1 = 2 > 0 và 2. 1  = 2 > 0 nên cặp số (1; 1) không là nghiệm của bất phương trình 2x ≤ 0.

Suy ra điểm P(1; 1) không thuộc miền nghiệm của hệ $\left\{\begin{array}{l}-x+3y\ge 0\\ 2x\le 0\end{array}\right.$.

Vậy khẳng định D là sai.

Vậy ta chọn đáp án A.

Câu 3. Tìm khẳng định sai trong các khẳng định sau:

A. Hệ $\left\{\begin{array}{l}x+y\ge -1\\ y^2-1\le 0\end{array}\right.$ không phải là hệ bất phương trình bậc nhất hai ẩn;

B. Hệ $\left\{\begin{array}{l}x\ge 1+y\\ 5x+y<0\end{array}\right.$ là hệ bất phương trình bậc nhất hai ẩn;

C. Hệ $\left\{\begin{array}{l}x+1+y>0\\ x^2+y<0\end{array}\right.$ là hệ bất phương trình bậc nhất hai ẩn;

D. Hệ $\left\{\begin{array}{l}\frac{1}{2}x+2y<7\\ x+3y\le 0\end{array}\right.$ là hệ bất phương trình bậc nhất hai ẩn;

Đáp án đúng là: C

+ Vì $\left\{\begin{array}{l}x+y\ge -1\\ y^2-1\le 0\end{array}\right.$ chứa bất phương trình bậc hai y² – 1 ≤ 0 nên hệ này không phải là hệ bất phương trình bậc nhất hai ẩn.

Do đó khẳng định A đúng.

+ Vì $\left\{\begin{array}{l}x\ge 1+y\\ 5x+y<0\end{array}\right.$ chứa hai bất phương trình x ≥ 1 + y và 5x + y < 0 đều là các bất phương trình bậc nhất hai ẩn, nên hệ này là hệ bất phương trình bậc nhất hai ẩn.

Do đó khẳng định B đúng.

+ Vì $\left\{\begin{array}{l}x+1+y>0\\ x^2+y<0\end{array}\right.$ chứa bất phương trình bậc hai x² + y < 0 nên hệ này không phải là hệ bất phương trình bậc nhất hai ẩn.

Do đó khẳng định C sai.

+ Vì $\left\{\begin{array}{l}\frac{1}{2}x+2y<7\\ x+3y\le 0\end{array}\right.$chứa hai bất phương trình $\frac{1}{2}x+y<7$ và x + 3y ≤ 0 đều là các bất phương trình bậc nhất hai ẩn nên hệ này là hệ bất phương trình bậc nhất hai ẩn.

Do đó khẳng định D đúng.

Vậy ta chọn đáp án C.

Câu 4. Cho hệ bất phương trình $\left\{\begin{array}{l}-x+2y\ge 2\\ 2x+y\le -1\end{array}\right.$. Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?

A. M(0; 1);         

B. N(–1; 1);        

C. P(–1; 4);        

D. Q(1; 3).

Đáp án đúng là: B

+ Ta có : –0 + 2.1 = 2 và 2.0 + 1 = 1 > –1.

Do đó cặp số (0; 1) không là nghiệm của bất phương trình 2x + y ≤ –1.

Vậy nên cặp số (0; 1) không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+2y\ge 2\\ 2x+y\le -1\end{array}\right.$.

Suy ra điểm M(0; 1) không thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+2y\ge 2\\ 2x+y\le -1\end{array}\right.$

+ Ta có : –(–1) +2.1 = 3 > 2 và 2.(–1) + 1 = –1.

Do đó cặp số (–1; 1) là nghiệm của cả hai bất phương trình –x + 3y ≥2 và 2x + y ≤ –1.

Vậy nên, cặp số (–1; 1) là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+2y\ge 2\\ 2x+y\le -1\end{array}\right.$.

Suy ra điểm N(–1; 1) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+2y\ge 2\\ 2x+y\le -1\end{array}\right.$.

+ Ta có : –(–1) + 2.4 = 9 > 2 và 2.(–1) + 4 = 2 > –1.

Do đó cặp số (–1; 4) không là nghiệm của bất phương trình 2x + y ≤ –1.

Vậy nên cặp số (–1; 4) không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+2y\ge 2\\ 2x+y\le -1\end{array}\right.$.

Suy ra điểm P(–1; 4) không thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+2y\ge 2\\ 2x+y\le -1\end{array}\right.$

+ Ta có : –1 + 2.3 = 5 > 2 và 2.1 + 3 = 5 > –1.

Do đó cặp số (1; 3) không là nghiệm của bất phương trình 2x + y ≤ –1.

Vậy nên cặp số (1; 3) không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+2y\ge 2\\ 2x+y\le -1\end{array}\right.$.

Suy ra điểm Q(1; 3) không thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x+2y\ge 2\\ 2x+y\le -1\end{array}\right.$

Vậy điểm N(–1; 1) thuộc miền nghiệm của hệ bất phương trình đã cho nên ta chọn đáp án B.

Câu 5. Cho hệ bất phương trình $\left\{\begin{array}{l}-3x+y>-2\\ x+2y\le 1\end{array}\right.$. Và các điểm sau: M(–1 ; 2), N(0; –1), O(0; 0). Có mấy điểm thuộc miền nghiệm của hệ bất phương trình đã cho?

A. 0;

B. 1;  

C. 2;

D. 3.

Đáp án đúng là: C

+ Ta có : –3. (–1)  + 2 = 5 > –2 và –1 + 2.2 = 3 > 1.

Do đó cặp số (–1 ; 2) không là nghiệm của bất phương trình x + 2y ≤ 1.

Vậy nên cặp số (–1 ; 2) không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-3x+y>-2\\ x+2y\le 1\end{array}\right.$.

Suy ra điểm M(–1 ; 2) không thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-3x+y>-2\\ x+2y\le 1\end{array}\right.$.

+ Ta có : –3. 0 +  (–1)= –1 > –2 và 0 + 2. (–1) = –2 < 1.

Do đó cặp số (0; –1) là nghiệm của cả hai bất phương trình –3x  + y > –2 và x + 2y ≤ 1.

Vậy nên cặp số (0; –1) là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-3x+y>-2\\ x+2y\le 1\end{array}\right.$.

Suy ra điểm M(0; –1)  thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-3x+y>-2\\ x+2y\le 1\end{array}\right.$.

+ Ta có : –3. 0  + 0 = 0 > –2 và 0 + 2.0 = 0 < 1.

Do đó cặp số (0 ; 0) là nghiệm của cả hai bất phương trình –3x  + y > –2 và x + 2y ≤ 1.

Vậy nên cặp số (0 ; 0) là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-3x+y>-2\\ x+2y\le 1\end{array}\right.$.

Suy ra điểm O(0 ; 0) thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-3x+y>-2\\ x+2y\le 1\end{array}\right.$.

Vậy hai điểm M(0; –1)  và O(0 ; 0) thuộc miền nghiệm của hệ $\left\{\begin{array}{l}-3x+y>-2\\ x+2y\le 1\end{array}\right.$.

Do đó ta chọn đáp án C.

Câu 6. Cặp số (0; –3) là nghiệm của hệ bất phương trình nào sau đây?

A. $\left\{\begin{array}{l}x-y\le 1\\ x+3y\le 3x-4\end{array}\right.$

B. $\left\{\begin{array}{l}2x-y>0\\ 2x+y>1\end{array}\right.$

C. $\left\{\begin{array}{l}-x-4y>-3\\ 2x+y\le 2\end{array}\right.$

D. $\left\{\begin{array}{l}2x-y\le -3\\ 5y\ge -1\end{array}\right.$

Đáp án đúng là: C

+ Ta có : 0 – (–3)= 3 > 1 và 0 + 3. (–3) < 3.0 – 4  (–9 < –4) là mệnh đề đúng.

Do đó cặp số (0; –3) không là nghiệm của bất phương trình x  – y  ≤ –1.

Vậy nên cặp số (0; –3) không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x-y\le 1\\ x+3y\le 3x-4\end{array}\right.$.

+ Ta có : 2.0 – (–3)= 3 > 0 và 2.0 + (–3) = – 3 < 1.

Do đó cặp số (0; –3) không là nghiệm của bất phương trình 2x  + y  > 1.

Vậy nên cặp số (0; –3) không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}2x-y>0\\ 2x+y>1\end{array}\right.$.

+ Ta có : –0 – 4.(–3)= 12 > – 3 và 2.0 + (–3) = – 3 < 2.

Do đó cặp số (0; –3) là nghiệm của cả hai bất phương trình –x –4y > –3 và 2x  + y  ≤ 2.

Vậy nên cặp số (0; –3) là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x-4y>-3\\ 2x+y\le 2\end{array}\right.$.

+ Ta có : 2.0 – (–3)= 3 > – 3 và 5. (–3) = – 15 <– 1.

Do đó cặp số (0; –3) không là nghiệm của cả hai bất phương trình 2x  – y  ≤ –3 và 5y ≥ –1.

Vậy nên cặp số (0; –3) không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}2x-y\le -3\\ 5y\ge -1\end{array}\right.$.

Vậy nên cặp số (0; –3) là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}-x-4y>-3\\ 2x+y\le 2\end{array}\right.$

Do đó ta chọn đáp án C.

Câu 7. Cho hai điểm M(1; 0) và N(–2; –1) và hệ bất phương trình $\left\{\begin{array}{l}2x\le 1\\ 2x+5y<3\end{array}\right.$. Trong hai điểm M và N, điểm nào thuộc miền nghiệm của hệ đã cho?

A. Cả M và N đều không thuộc miền nghiệm của hệ đã cho.

B. Điểm M thuộc miền nghiệm còn N không thuộc miền nghiệm của hệ đã cho.

C. Điểm M không thuộc miền nghiệm còn N thuộc miền nghiệm của hệ đã cho.

D. Cả hai điểm M và N đều thuộc miền nghiệm của hệ đã cho.

Đáp án đúng là: C

+ Ta có : 2.1 = 2 > 1 và 2. 1 + 5. 0 = 2 < 3.

Do đó cặp số (1; 0) không là nghiệm của bất phương trình 2x  ≤ 1.

Suy ra cặp số (1; 0) không là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}2x\le 1\\ 2x+5y<3\end{array}\right.$.

Vậy nên, điểm M(1; 0) không thuộc miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}2x\le 1\\ 2x+5y<3\end{array}\right.$

+ Ta có : 2. (–2) = –4 < 1 và 2. (–2) + 5. (–1) = –9 < 3.

Do đó cặp số (–2; –1) là nghiệm của của hai bất phương trình 2x  ≤ 1 và 2x + 5y < 3.

Suy ra cặp số (–2; –1) là nghiệm của hệ bất phương trình $\left\{\begin{array}{l}2x\le 1\\ 2x+5y<3\end{array}\right.$.

Vậy nên, điểm N(–2; –1) thuộc miền nghiệm của hệ bất phương trình  $\left\{\begin{array}{l}2x\le 1\\ 2x+5y<3\end{array}\right.$.

Do đó điểm M không thuộc miền nghiệm, điểm N thuộc miền nghiệm của hệ đã cho. Vậy ta chọn đáp án C.

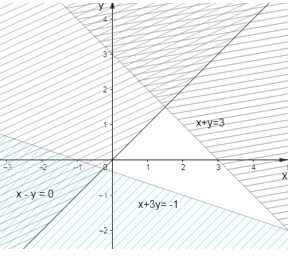
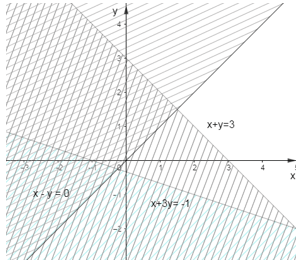
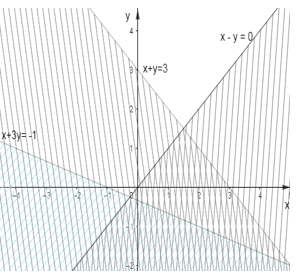
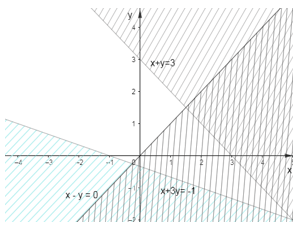
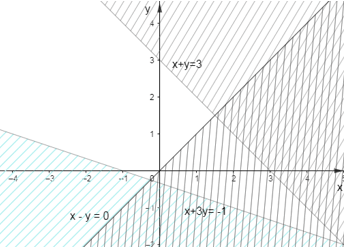
Câu 8. Miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x-y<0\\ x+3y>-1\\ x+y<3\end{array}\right.$ là miền không gạch chéo (không kể bờ) của hình vẽ nào trong các hình vẽ sau?

A.

B.

C.

D.

Đáp án đúng là: D

+ Ta có 0 – 1=  –1 < 0 nên điểm (0 ; 1) thuộc miền nghiệm của bất phương trình x – y < 0 .

Do đó miền nghiệm của bất phương trình x – y < 0 là nửa mặt phẳng bờ là đường thẳng x – y = 0, chứa điểm (0; 1) (không chứa bờ).

+ Ta có 0 + 3.0 = 0 > –1 nên điểm O(0 ; 0) thuộc miền nghiệm của bất phương trình x + 3y > –1 .

Do đó miền nghiệm của bất phương trình x + 3y > –1 là nửa mặt phẳng bờ là đường thẳng x + 3y = –1, chứa điểm O (không chứa bờ).

+ Ta có 0 + 0 = 0 < 3 nên điểm O(0 ; 0) thuộc miền nghiệm của bất phương trình x + y < 3.

Do đó miền nghiệm của bất phương trình x + y < 3 là nửa mặt phẳng có bờ là đường thẳng x + y = 3, chứa điểm O (không chứa bờ).

Ta có hình ảnh biểu diễn miền nghiệm của hệ là miền không gạch chéo trong hình sau:

Do đó ta chọn đáp án D.

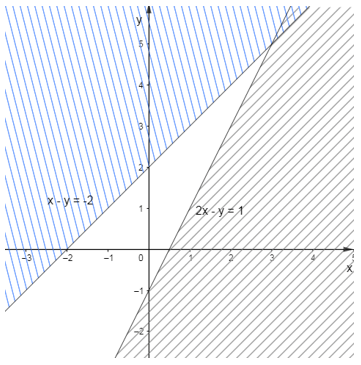
Câu 9. Miền không gạch chéo trong hình vẽ dưới đây (không chứa bờ), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?

A. $\left\{\begin{array}{l}x-y\ge -2\\ 2x-y\ge 1\end{array}\right.$  

B. $\left\{\begin{array}{l}x-y>-2\\ 2x-y<1\end{array}\right.$

C. $\left\{\begin{array}{l}x-y<-2\\ 2x-y>1\end{array}\right.$

D. $\left\{\begin{array}{l}x-y<-2\\ 2x-y<1\end{array}\right.$

Đáp án đúng là: B

Đường thẳng x – y = –2 chia mặt phẳng tọa độ thành hai nửa mặt phẳng.

Xét điểm O(0; 0), ta có : 0 – 0 = 0 > –2 .

Mặt khác điểm O thuộc miền nghiệm của hệ bất phương trình cần tìm. Do đó ta có bất phương trình thứ nhất của hệ là x – y > –2.

Đường thẳng 2x – y = 1 chia mặt phẳng tọa độ thành hai nửa mặt phẳng.

Xét điểm O(0; 0), ta có : 2.0 – 0 = 0 < 1 .

Mặt khác điểm O thuộc miền nghiệm của hệ bất phương trình cần tìm. Do đó ta có bất phương trình thứ hai của hệ là 2x – y < 1.

Suy ra hệ cần tìm là: $\left\{\begin{array}{l}x-y>-2\\ 2x-y<1\end{array}\right.$

Ta chọn đáp án B.

Xem thêm các dạng bài tập hay, có đáp án: