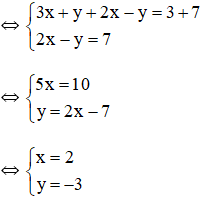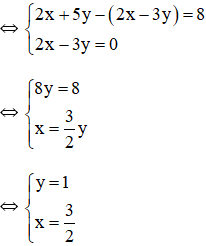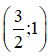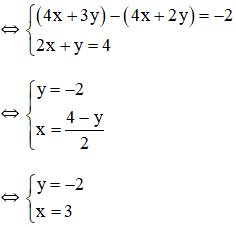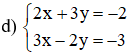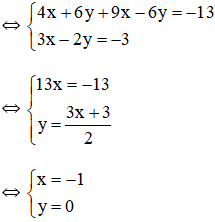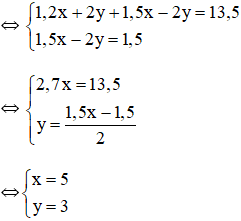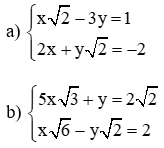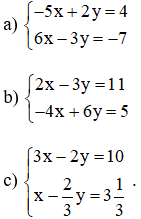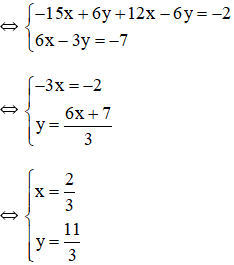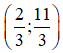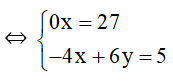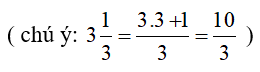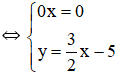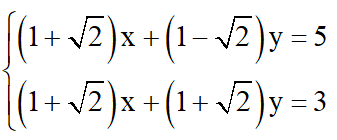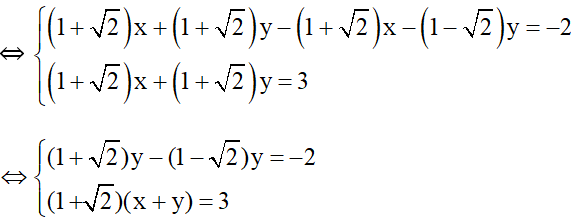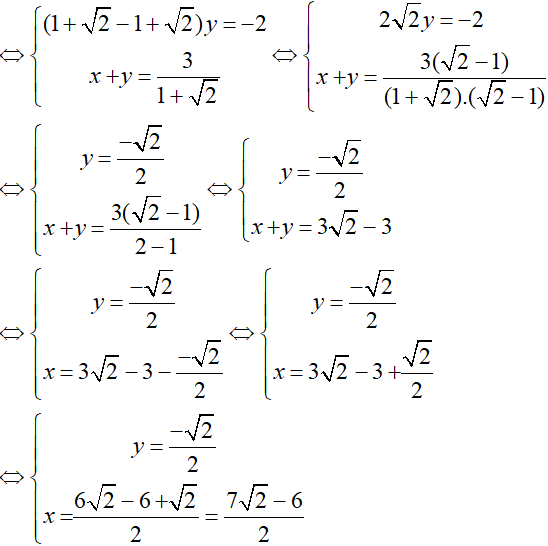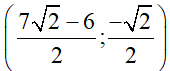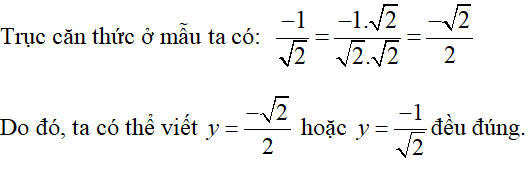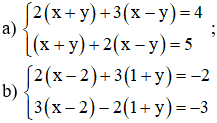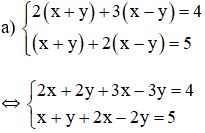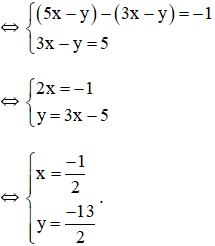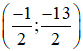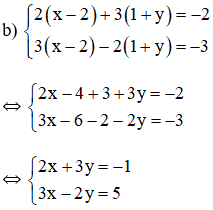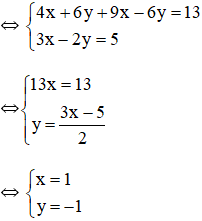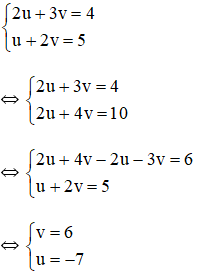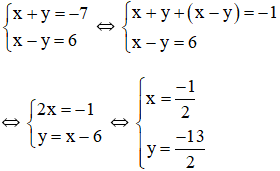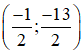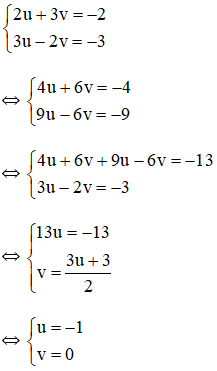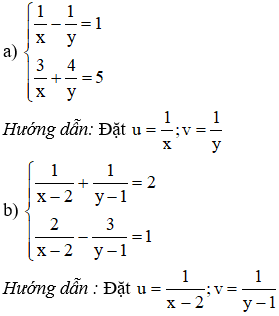50 Bài tập Giải hệ phương trình bằng phương pháp cộng đại số (có đáp án năm 2024) - Toán 9

Giải hệ phương trình bằng phương pháp cộng đại số

Kiến thức cần nhớ 

1. Quy tắc cộng đại số

Định nghĩa: Quy tắc cộng đại số dùng để biến đổi một hệ phương trình thành hệ phương trình tương đương.

Các bước cộng đại số:

Bước 1: Cộng hay trừ từng vế của hai phương trình đã cho để được phương trình mới.

Bước 2: Dùng phương trình mới đấy thay thế cho một trong hai phương trình của hệ (và giữ nguyên phương trình kia)

Ví dụ 1: Xét hệ phương trình $\left\{\begin{array}{l}2\mathrm{x}-\mathrm{y}=5\\ 3\mathrm{x}+\mathrm{y}=10\end{array}\right.$(I). Áp dụng quy tắc cộng đại số để biến đổi hệ phương trình.

Ta có: $\left\{\begin{array}{l}2\mathrm{x}-\mathrm{y}=5 \left(1\right)\\ 3\mathrm{x}+\mathrm{y}=10 \left(2\right)\end{array}\right.$.

Cộng vế với vế của phương trình (1) với phương trình (2) ta được hệ mới:

$$\begin{gathered} \left\{\begin{array}{l}\left(2\mathrm{x}-\mathrm{y}\right)+\left(3\mathrm{x}+\mathrm{y}\right)=5+10\\ 2\mathrm{x}-\mathrm{y}=5\end{array}\right. \\ \iff \left\{\begin{array}{l}2\mathrm{x}-\mathrm{y}+3\mathrm{x}+\mathrm{y}=15\\ 2\mathrm{x}-\mathrm{y}=5\end{array}\right. \\ \iff \left\{\begin{array}{l}5\mathrm{x}=15\\ 2\mathrm{x}-\mathrm{y}=5\end{array}\right. \end{gathered}$$

2. Giải hệ phương trình bằng phương pháp cộng đại số

a) Trường hợp thứ nhất: Các hệ số của cùng một ẩn nào đó trong hệ phương trình đã bằng nhau hoặc đối nhau

Bước 1: Cộng (trừ) vế với với của hai phương trình ban đầu với nhau đề được phương trình mới.

Bước 2: Viết lại hệ phương trình mới với một phương trình là phương trình mới sau khi đã cộng (trừ) đại số và một phương trình là phương trình ban đầu của hệ. Giải hệ phương trình.

Ví dụ 2: Xét hệ phương trình: $\left\{\begin{array}{l}\mathrm{x}+3\mathrm{y}=5\\ 4\mathrm{x}+3\mathrm{y}=11\end{array}\right.$

Ta có: $\left\{\begin{array}{l}\mathrm{x}+3\mathrm{y}=5 \left(1\right)\\ 4\mathrm{x}+3\mathrm{y}=11 \left(2\right)\end{array}\right.$

Trừ vế với vế của phương trình (1) cho phương trình (2) ta được hệ phương trình mới:

$$\begin{gathered} \left\{\begin{array}{l}\left(\mathrm{x}+3\mathrm{y}\right)-\left(4\mathrm{x}+3\mathrm{y}\right)=5-11\\ \mathrm{x}+3\mathrm{y}=5\end{array}\right. \\ \iff \left\{\begin{array}{l}\mathrm{x}+3\mathrm{y}-4\mathrm{x}-3\mathrm{y}=-6\\ \mathrm{x}+3\mathrm{y}=5\end{array}\right. \\ \iff \left\{\begin{array}{l}-3\mathrm{x}=-6\\ \mathrm{x}+3\mathrm{y}=5\end{array}\iff \left\{\begin{array}{l}\mathrm{x}=\left(-6\right):\left(-3\right)\\ \mathrm{x}+3\mathrm{y}=5\end{array}\right.\right. \\ \iff \left\{\begin{array}{l}\mathrm{x}=2\\ 2+3\mathrm{y}=5\end{array}\iff \left\{\begin{array}{l}\mathrm{x}=2\\ 3\mathrm{y}=5-2\end{array}\right.\right. \\ \iff \left\{\begin{array}{l}\mathrm{x}=2\\ 3\mathrm{y}=3\end{array}\iff \left\{\begin{array}{l}\mathrm{x}=2\\ \mathrm{y}=1\end{array}\right.\right. \end{gathered}$$

Vậy hệ phương trình đã cho có nghiệm (x; y) là (2; 1).

b) Trường hợp thứ 2: Các hệ số của mỗi ẩn trong phương trình không bằng nhau hoặc không đối nhau

Bước 1: Nhân hai vế của mỗi phương trình với các số thích hợp sao cho với một ẩn nào đó các hệ số bằng nhau hoặc đối nhau.

Bước 2: Cộng (trừ) vế với với của hai phương trình ban đầu với nhau đề được phương trình mới.

Bước 3: Viết lại hệ phương trình mới với một phương trình là phương trình mới sau khi đã cộng (trừ) đại số và một phương trình là phương trình ban đầu của hệ. Giải hệ phương trình.

Ví dụ 3: Xét hệ phương trình $\left\{\begin{array}{l}2\mathrm{x}+3\mathrm{y}=5 \left(1\right)\\ 3\mathrm{x}+2\mathrm{y}=7 \left(2\right)\end{array}\right.$

Nhân hai vế của phương trình (1) với 3 và hai vế của phương trình (2) với 2 ta được hệ mới

$$\begin{gathered} \left\{\begin{array}{l}3.\left(2\mathrm{x}+3\mathrm{y}\right)=3.5\\ 2.\left(3\mathrm{x}+2\mathrm{y}\right)=2.7\end{array}\right. \\ \iff \left\{\begin{array}{l}6\mathrm{x}+9\mathrm{y}=15\\ 6\mathrm{x}+4\mathrm{y}=14\end{array}\right. \end{gathered}$$

Bài tập tự luyện 

Bài 1: Giải các hệ phương trình sau bằng phương pháp cộng đại số:

Lời giải

(Các phần giải thích học sinh không phải trình bày).

 (Vì hệ số của y ở 2 pt đối nhau nên cộng từng vế của 2 pt).

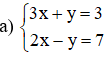
Vậy hệ phương trình có nghiệm duy nhất (2; -3).

 (Hệ số của x ở 2 pt bằng nhau nên ta trừ từng vế của 2pt)

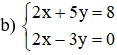
Vậy hệ phương trình có nghiệm duy nhất 

 (Nhân cả hai vế của pt 2 với 2 để hệ số của x bằng nhau)

 (Hệ số của x bằng nhau nên ta trừ từng vế của 2 pt)

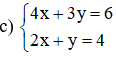
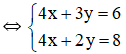
Vậy hệ phương trình có nghiệm duy nhất (3; -2).

(Nhân hai vế pt 1 với 2, pt 2 với 3 để hệ số của y đối nhau)

 (Hệ số của y đối nhau nên cộng từng vế hai phương trình).

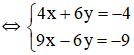
Vậy hệ phương trình có nghiệm duy nhất (-1; 0).

 (Nhân hai vế pt 1 với 4 để hệ số của y đối nhau)

 (Hệ số của y đối nhau nên ta cộng từng vế 2pt)

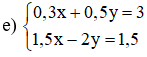
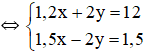
Vậy hệ phương trình có nghiệm duy nhất (5; 3).

Bài 2: Giải các hệ phương trình sau bằng phương pháp cộng đại số:

Lời giải

a) $\left\{\begin{array}{l}x\sqrt{2}-3y=1\\ 2x+y\sqrt{2}=-2\end{array}\right.$

$\iff \left\{\begin{array}{l}2x-3\sqrt{2}y=\sqrt{2}\\ 2x+y\sqrt{2}=-2\end{array}\right.$ (nhân của hai vế phương trình thứ nhất với $\sqrt{2}$)

$\iff \left\{\begin{array}{l}2x-3\sqrt{2}y=\sqrt{2}\\ \left(2x-3\sqrt{2}y\right)-\left(2x+\sqrt{2}y\right)=\sqrt{2}+2\end{array}\right.$ (trừ vế với vế của phương trình thứ nhất với phương trình thứ hai).

$\iff \left\{\begin{array}{l}2x-3\sqrt{2}y=\sqrt{2}\\ 2x-3\sqrt{2}y-2x-\sqrt{2}y=\sqrt{2}+2\end{array}\right.$

$\iff \left\{\begin{array}{l}2x-3\sqrt{2}y=\sqrt{2}\\ -4\sqrt{2}y=\sqrt{2}+2\end{array}\right.$

$\iff \left\{\begin{array}{l}2x-3\sqrt{2}y=\sqrt{2}\\ y=\frac{\sqrt{2}+2}{-4\sqrt{2}}\end{array}\right.$

$\iff \left\{\begin{array}{l}2x-3\sqrt{2}y=\sqrt{2}\\ y=-\frac{1+\sqrt{2}}{4}\end{array}\right.$

$\iff \left\{\begin{array}{l}2x-3\sqrt{2}.\left(-\frac{1+\sqrt{2}}{4}\right)=\sqrt{2}\\ y=-\frac{1+\sqrt{2}}{4}\end{array}\right.$

$\iff \left\{\begin{array}{l}2x+\frac{6+3\sqrt{2}}{4}=\sqrt{2}\\ y=-\frac{1+\sqrt{2}}{4}\end{array}\right.$

$\iff \left\{\begin{array}{l}2x=\sqrt{2}-\frac{6+3\sqrt{2}}{4}\\ y=-\frac{1+\sqrt{2}}{4}\end{array}\right.$

$\iff \left\{\begin{array}{l}2x=\frac{-6+\sqrt{2}}{4}\\ y=-\frac{1+\sqrt{2}}{4}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{-6+\sqrt{2}}{8}\\ y=-\frac{1+\sqrt{2}}{4}\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(\frac{\sqrt{2}-6}{8};\frac{-\sqrt{2}-1}{4}\right)$

b)$\left\{\begin{array}{l}5x\sqrt{3}+y=2\sqrt{2}\\ x\sqrt{6}-y\sqrt{2}=2\end{array}\right.$ (nhân cả hai vế phương trình 1 với $\sqrt{2}$)

$\iff \left\{\begin{array}{l}5x\sqrt{3}.\sqrt{2}+\sqrt{2}y=2\sqrt{2}.\sqrt{2}\\ x\sqrt{6}-y\sqrt{2}=2\end{array}\right.$

$\iff \left\{\begin{array}{l}5x\sqrt{6}+\sqrt{2}y=4\\ x\sqrt{6}-\sqrt{2}y=2\end{array}\right.$

$\iff \left\{\begin{array}{l}x\sqrt{6}-\sqrt{2}y=2\\ \left(5x\sqrt{6}+\sqrt{2}y\right)+\left(x\sqrt{6}-\sqrt{2}y\right)=4+2\end{array}\right.$

$\iff \left\{\begin{array}{l}x\sqrt{6}-\sqrt{2}y=2\\ 5x\sqrt{6}+\sqrt{2}y+x\sqrt{6}-\sqrt{2}y=6\end{array}\right.$

$\iff \left\{\begin{array}{l}x\sqrt{6}-\sqrt{2}y=2\\ 6\sqrt{6}x=6\end{array}\right.$

$\iff \left\{\begin{array}{l}x\sqrt{6}-\sqrt{2}y=2\\ x=6:6\sqrt{6}\end{array}\right.$

$\iff \left\{\begin{array}{l}x\sqrt{6}-\sqrt{2}y=2\\ x=\frac{\sqrt{6}}{6}\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{\sqrt{6}}{6}\\ \sqrt{6}.\frac{\sqrt{6}}{6}-\sqrt{2}y=2\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{\sqrt{6}}{6}\\ 1-\sqrt{2}y=2\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{\sqrt{6}}{6}\\ \sqrt{2}y=-1\end{array}\right.$

$\iff \left\{\begin{array}{l}x=\frac{\sqrt{6}}{6}\\ y=\frac{-\sqrt{2}}{2}\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(\frac{\sqrt{6}}{6};\frac{-\sqrt{2}}{2}\right)$.

Bài 3: Giải các hệ phương trình sau bằng phương pháp cộng đại số:

Lời giải

(Các phần giải thích học sinh không phải trình bày).

 (Nhân 2 vế pt 1 với 3; nhân pt 2 với 2 để hệ số của y đối nhau)

 (hệ số của y đối nhau nên ta cộng từ vế 2 pt)

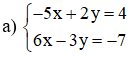
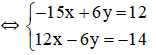
Vậy hệ phương trình có nghiệm duy nhất 

 (Nhân hai vế pt 1 với 2 để hệ số của y đối nhau)

 ( lấy vế cộng vế hai phương trình)

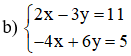
Phương trình 0x = 27 vô nghiệm nên hệ phương trình vô nghiệm.

 (Nhân hai vế pt 2 với 3 để hệ số của y bằng nhau)

 (Trừ từng vế hai phương trình)

Phương trình 0x = 0 nghiệm đúng với mọi x.

Vậy hệ phương trình có vô số nghiệm dạng  (x ∈ R).

Bài 4: Giải hệ phương trình sau:

Lời giải

Lấy phương trình (2) trừ phương trình (1), vế trừ vế ta được:

Vậy hệ phương trình có nghiệm duy nhất 

Lưu ý:

Bài 5: Giải các hệ phương trình sau:

Lời giải

Bài toán này có hai cách giải:

Cách 1: Thu gọn từng phương trình ta sẽ thu được phương trình bậc nhất hai ẩn x và y.

Cách 2: Đặt ẩn phụ.

Cách 1:

 (hệ số của y bằng nhau nên ta trừ từng vế hai phương trình)

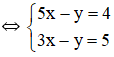
Vậy hệ phương trình có nghiệm duy nhất 

(Nhân hai vế pt 1 với 2; pt 2 với 3 để hệ số của y đối nhau)

 (Hệ số của y đối nhau nên ta cộng từng vế của hai pt)

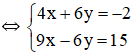
Vậy hệ phương trình có nghiệm duy nhất (1; -1).

Cách 2:

a) Đặt x + y = u và x – y = v (*)

Khi đó hệ phương trình trở thành

Thay u = -7 và v = 6 vào (*) ta được hệ phương trình:

Vậy hệ phương trình có nghiệm 

b) Đặt x – 2 = u và y + 1 = v.

Khi đó hệ phương trình trở thành :

+ u = -1 ⇒ x – 2 = -1 ⇒ x = 1.

+ v = 0 ⇒ y + 1 = 0 ⇒ y = -1.

Vậy hệ phương trình có nghiệm (1; -1).

Bài 6: Ta biết rằng: Một đa thức bằng đa thức 0 khi và chỉ khi tất cả các hệ số của nó bằng 0. Hãy tìm các giá trị của m và n để đa thức sau (với biến số x) bằng đa thức 0:

P(x) = (3m – 5n + 1)x + (4m – n -10)

Lời giải

Đa thức P(x) bằng đa thức 0

Vậy với m = 3 vào n = 2 thì đa thức P(x) bằng đa thức 0.

Bài 7: Xác định a và b để đồ thị của hàm số y = ax + b đi qua hai điểm A và B trong mỗi trường hợp sau:

a) A(2; -2) và B(-1; 3) ;     b) A(-4; -2) và B(2; 1)

c) A(3; -1) và B(-3; 2) ;     d) A(√3; 2) và B(0; 2)

Lời giải

a) Đồ thị hàm số y = ax + b đi qua A(2; -2). Thay x = 2 và y = -2 vào hàm số ta có:

2.a + b = -2 (1)

Đồ thị hàm số y = ax + b đi qua B(-1 ; 3). Thay x = -1; y = 3 vào hàm số ta có:

a.(-1) + b = 3 (2)

Từ (1) và (2) ta có hệ phương trình :

$\left\{\begin{array}{l}2a+b=-2\\ -a+b=3\end{array}\right.\iff \left\{\begin{array}{l}2a+b=-2\\ \left(2a+b\right)-\left(-a+b\right)=-2-3\end{array}\right.$

$\iff \left\{\begin{array}{l}2a+b=-2\\ 2a+b+a-b=-5\end{array}\right.$ $\iff \left\{\begin{array}{l}2a+b=-2\\ 3a=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}2a+b=-2\\ a=-5:3\end{array}\right.$ $\iff \left\{\begin{array}{l}a=\frac{-5}{3}\\ 2.\left(\frac{-5}{3}\right)+b=-2\end{array}\right.$

$\iff \left\{\begin{array}{l}a=\frac{-5}{3}\\ \frac{-10}{3}+b=-2\end{array}\right.$ $\iff \left\{\begin{array}{l}a=\frac{-5}{3}\\ b=-2+\frac{10}{3}\end{array}\right.$

$\iff \left\{\begin{array}{l}a=\frac{-5}{3}\\ b=\frac{4}{3}\end{array}\right.$

Vậy a = $\frac{-5}{3}$; b = $\frac{4}{3}$.

b) Đồ thị hàm số y = ax + b đi qua A(-4; -2). Thay x = -4; y = -2 vào hàm số ta được:

 a.(-4) + b = -2 (3)

Đồ thị hàm số y = ax + b đi qua B(2 ; 1). Thay x = 2 ; y = 1 vào hàm số ta được:

a.2 + b = 1 (4)

Từ (3) và (4) ta có hệ phương trình:

$\left\{\begin{array}{l}-4a+b=-2\\ 2a+b=1\end{array}\right.$ $\iff \left\{\begin{array}{l}\left(-4a+b\right)-\left(2a+b\right)=-2-1\\ 2a+b=1\end{array}\right.$

$\iff \left\{\begin{array}{l}-4a+b-2a-b=-3\\ 2a+b=1\end{array}\right.$

$\iff \left\{\begin{array}{l}-6a=-3\\ 2a+b=1\end{array}\right.$ $\iff \left\{\begin{array}{l}a=\frac{1}{2}\\ 2.\frac{1}{2}+b=1\end{array}\right.$

$\iff \left\{\begin{array}{l}a=\frac{1}{2}\\ 1+b=1\end{array}\right.\iff \left\{\begin{array}{l}a=\frac{1}{2}\\ b=0\end{array}\right.$

Vậy a = $\frac{1}{2}$ và b = 0

c) Đồ thị hàm số y = ax + b đi qua A(3 ; -1). Thay x = 3 và y = -1 vào hàm số ta được:

a.3 + b = -1 (5)

Đồ thị hàm số y = ax + b đi qua B(-3 ; 2). Thay x = -3; y = 2 vào hàm số ta được: 

a.(-3) + b = 2 (6)

Ta có hệ phương trình :

Từ (5) và (6) ta có hệ phương trình:

$\left\{\begin{array}{l}3a+b=-1\\ -3a+b=2\end{array}\right.$ $\iff \left\{\begin{array}{l}3a+b=-1\\ \left(3a+b\right)+\left(-3a+b\right)=-1+2\end{array}\right.$

$\iff \left\{\begin{array}{l}3a+b=-1\\ 3a+b-3a+b=1\end{array}\right.$ $\iff \left\{\begin{array}{l}3a+b=-1\\ 2b=1\end{array}\right.$

$\iff \left\{\begin{array}{l}3a+\frac{1}{2}=-1\\ b=\frac{1}{2}\end{array}\right.$ $\iff \left\{\begin{array}{l}3a=-1-\frac{1}{2}\\ b=\frac{1}{2}\end{array}\right.$

$\iff \left\{\begin{array}{l}3a=\frac{-3}{2}\\ b=\frac{1}{2}\end{array}\right.$ $\iff \left\{\begin{array}{l}a=\frac{-3}{2}:3\\ b=\frac{1}{2}\end{array}\right.\iff \left\{\begin{array}{l}a=\frac{-1}{2}\\ b=\frac{1}{2}\end{array}\right.$

Vậy $a=\frac{-1}{2};b=\frac{1}{2}$

d) Đồ thị hàm số y = ax + b đi qua A $\left(\sqrt{3};2\right)$ .Thay x = $\sqrt{3}$; y = 2 ta có:

a.$\sqrt{3}$ + b = 2 (*)

Đồ thị hàm số y = ax + b đi qua B(0; 2). Thay x = 0 và y = 2 ta có:

a.0 + b = 2 ⇔ b = 2.

Thay b = 2 vào (*) ta được a.$\sqrt{3}$ + 2 = 2 ⇔ a.$\sqrt{3}$ = 0 ⇔ a = 0.

Vậy a = 0 và b = 2.

Bài 8: Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhất hai ẩn rồi giải:

Lời giải

a)$\left\{\begin{array}{l}\frac{1}{x}-\frac{1}{y}=1\\ \frac{3}{x}+\frac{4}{y}=5\end{array}\right.$ (I)

Đặt $\left\{\begin{array}{l}\frac{1}{x}=u\\ \frac{1}{y}=v\end{array}\right.$. Hệ phương trình (I) trở thành $\left\{\begin{array}{l}u-v=1\\ 3u+4v=5\end{array}\right.$

$\iff \left\{\begin{array}{l}3u-3v=3\\ 3u+4v=5\end{array}\right.$ $\iff \left\{\begin{array}{l}u-v=1\\ \left(3u-3v\right)-\left(3u+4v\right)=3-5\end{array}\right.$

$\iff \left\{\begin{array}{l}u-v=1\\ 3u-3v-3u-4v=-2\end{array}\right.$

$\iff \left\{\begin{array}{l}u-v=1\\ -7v=-2\end{array}\right.\iff \left\{\begin{array}{l}u=1+v\\ v=\frac{2}{7}\end{array}\right.$

$\iff \left\{\begin{array}{l}u=1+\frac{2}{7}\\ v=\frac{2}{7}\end{array}\right.\iff \left\{\begin{array}{l}u=\frac{9}{7}\\ v=\frac{2}{7}\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}\frac{1}{x}=\frac{9}{7}\\ \frac{1}{y}=\frac{2}{7}\end{array}\right.$ $\iff \left\{\begin{array}{l}x=\frac{7}{9}\\ y=\frac{7}{2}\end{array}\right.$

Vậy hệ phương trình có nghiệm (x; y) = $\left(\frac{7}{9};\frac{7}{2}\right)$

b)$\left\{\begin{array}{l}\frac{1}{x-2}+\frac{1}{y-1}=2\\ \frac{2}{x-2}-\frac{3}{y-1}=1\end{array}\right.$ (II)

Đặt $\left\{\begin{array}{l}\frac{1}{x-2}=u\\ \frac{1}{y-1}=v\end{array}\right.$. Khi đó hệ (II) trở thành $\left\{\begin{array}{l}u+v=2\\ 2u-3v=1\end{array}\right.$

$\iff \left\{\begin{array}{l}2u+2v=4\\ 2u-3v=1\end{array}\right.$ $\iff \left\{\begin{array}{l}u+v=2\\ \left(2u+2v\right)-\left(2u-3v\right)=4-1\end{array}\right.$

$\iff \left\{\begin{array}{l}u+v=2\\ 2u+2v-2u+3v=3\end{array}\right.$ $\iff \left\{\begin{array}{l}u+v=2\\ 5v=3\end{array}\right.$

$\iff \left\{\begin{array}{l}u+v=2\\ v=\frac{3}{5}\end{array}\right.\iff \left\{\begin{array}{l}u+\frac{3}{5}=2\\ v=\frac{3}{5}\end{array}\right.$

$\iff \left\{\begin{array}{l}u=2-\frac{3}{5}\\ v=\frac{3}{5}\end{array}\right.\iff \left\{\begin{array}{l}u=\frac{7}{5}\\ v=\frac{3}{5}\end{array}\right.$

$\iff \left\{\begin{array}{l}\frac{1}{x-2}=\frac{7}{5}\\ \frac{1}{y-1}=\frac{3}{5}\end{array}\right.\iff \left\{\begin{array}{l}7\left(x-2\right)=5\\ 3\left(y-1\right)=5\end{array}\right.$

$\iff \left\{\begin{array}{l}7x-14=5\\ 3y-3=5\end{array}\right.\iff \left\{\begin{array}{l}7x=14+5\\ 3y=5+3\end{array}\right.$

$\iff \left\{\begin{array}{l}7x=19\\ 3y=8\end{array}\right.\iff \left\{\begin{array}{l}x=\frac{19}{7}\\ y=\frac{8}{3}\end{array}\right.$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(\frac{19}{7};\frac{8}{3}\right)$.

Xem thêm các dạng bài tập toán hay khác:

50 Bài tập Giải bài toán bằng cách lập phương trình (có đáp án năm 2023)

50 Bài tập Hệ thức Vi – ét và ứng dụng (có đáp án năm 2023)

50 Bài tập Phương trình bậc hai một ẩn (có đáp án năm 2023)

50 Bài tập Giải bài toán bằng cách lập hệ phương trình (có đáp án năm 2023)

50 Bài tập Giải hệ phương trình bằng phương pháp cộng đại số (có đáp án năm 2023)