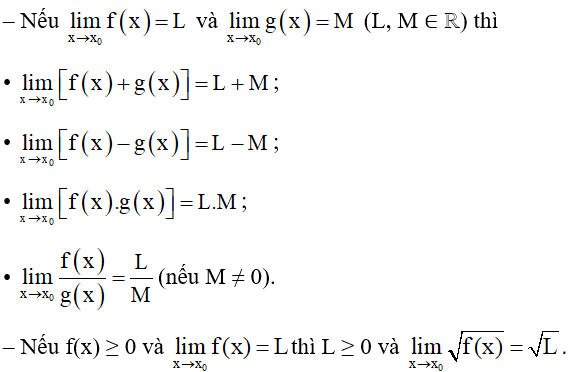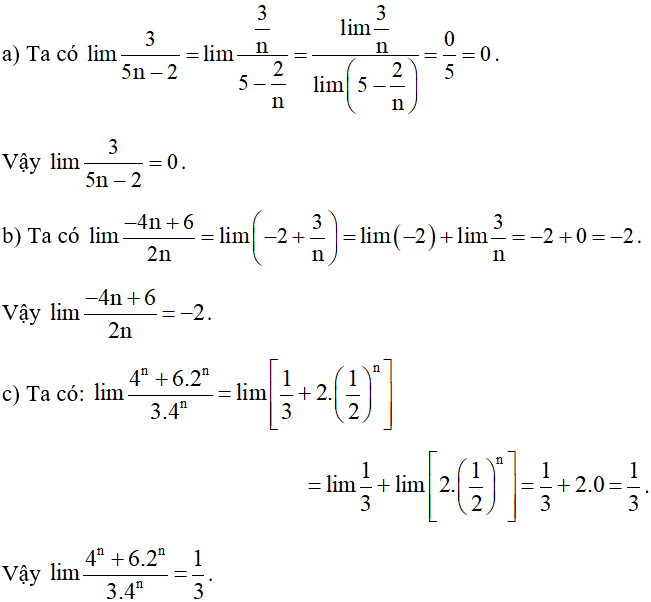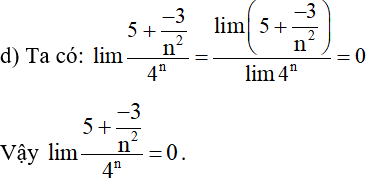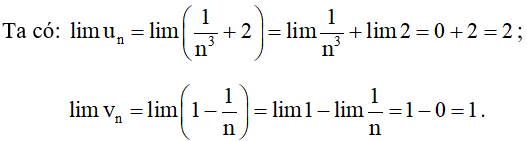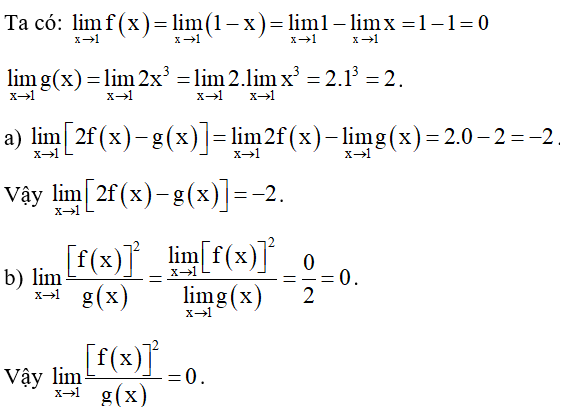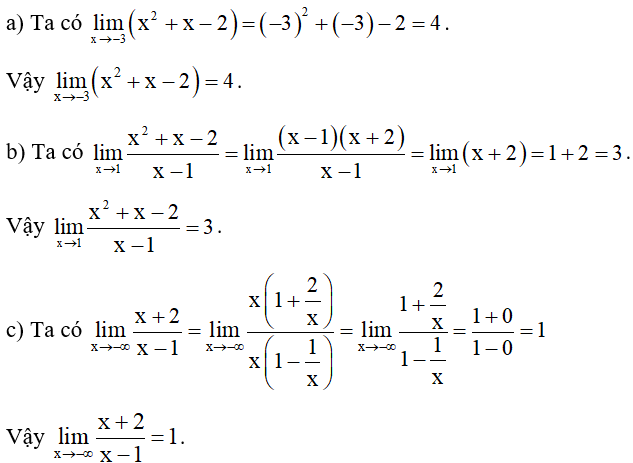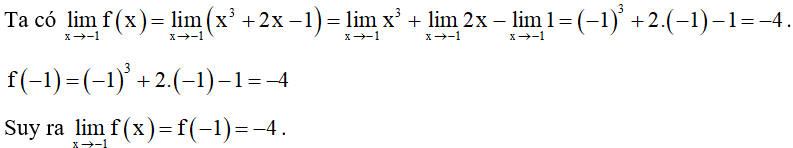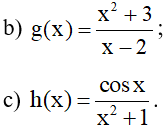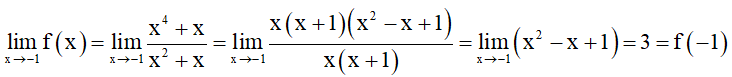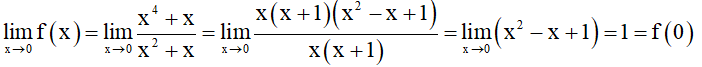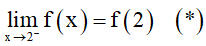Lý thuyết Toán 11 Chương 3: Giới hạn. Hàm số liên tục (Cánh diều)

Lý thuyết Toán 11 Chương 3: Giới hạn. Hàm số liên tục

1. Giới hạn của dãy số

1.1. Giới hạn hữu hạn của dãy số

a) Định nghĩa

– Dãy số (u_n) có giới hạn 0 khi n dần tới dương vô cực nếu |u_n| có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi, kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=0$.

– Dãy số (u_n) có giới hạn hữu hạn là a khi n dần tới dương vô cực nếu 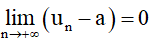 kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=\mathrm{a}$.

Nhận xét: Nếu u_n càng ngày càng gần tới 0 khi n ngày càng lớn thì lim u_n = 0.

Chú ý:

– Ngoài kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=0$, ta cũng sử dụng kí hiệu sau:

lim u_n = 0 hay u_n → 0 khi n → +∞.

– Ngoài kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=\mathrm{a}$, ta cũng sử dụng kí hiệu sau:

lim u_n = a hay u_n → a khi n → +∞.

– Một dãy số có giới hạn thì giới hạn đó là duy nhất.

– Không phải dãy số nào cũng có giới hạn, chẳng hạn như dãy số (u_n) với u_n = (–1)ⁿ.

b) Một số giới hạn cơ bản

Ta thừa nhận các giới hạn sau:

• $\lim \frac{1}{n}=0$; $\lim \frac{1}{n^k}=0$ với k là số nguyên dương cho trước;

• $\lim \frac{\mathrm{c}}{n}=0$; $\lim \frac{\mathrm{c}}{n^k}=0$ với c là hằng số, k là số nguyên dương cho trước;

• Nếu |q| < 1 thì lim qⁿ = 0;

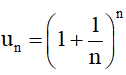
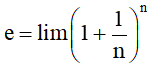
• Dãy số (u_n) với có giới hạn là một số vô tỉ và gọi giới hạn đó là e,

.

Một giá trị gần đúng của e là 2,718281828459045.

1.2. Định lí về giới hạn hữu hạn

a) Nếu lim u_n = a,  lim v_n = b thì:

lim (u_n + v_n) = a + b;

lim (u_n – v_n) = a – b;

lim (u_n . v_n) = a . b;

.

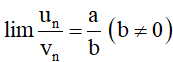
b) Nếu u_n ≥ 0 với mọi n và lim u_n = a thì a ≥ 0 và $\lim \sqrt{u_n}=\sqrt{a}$.

1.3. Tổng của cấp số nhân lùi vô hạn

Cấp số nhân vô hạn u₁, u₁q, …., u₁q^{n – 1}, … có công bội q thỏa mãn |q| < 1 được gọi là cấp số nhân lùi vô hạn.

Tổng của cấp số nhân lùi vô hạn đã cho là:

$S=u_1+u_{1}q+\mathrm{....}+u_1{q}^{n-1}+\mathrm{...}=\frac{u_1}{1-q}$.

1.4. Giới hạn vô cực

Định nghĩa dãy số có giới hạn vô cực:

– Ta nói dãy số (u_n) có giới hạn + ∞ khi n dần tới dương vô cực, nếu u_n có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.

Kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=+\infty$ hay $\lim u_n=+\infty$ hay u_n → + ∞ khi n → + ∞.

– Ta nói dãy số (u_n) có giới hạn –∞ khi n dần tới dương vô cực, nếu .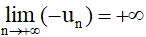

Kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=-\infty$ hay $\lim u_n=-\infty$ hay u_n → – ∞ khi n → + ∞.

Nhận xét:

• lim n^k = + ∞ với k là số nguyên dương cho trước.

• lim qⁿ = + ∞ với q > 1 là số thực cho trước.

• Nếu lim u_n = a và lim |v_n| = + ∞  thì $\lim \frac{u_n}{v_n}=0$.

• Nếu lim u_n = a, a > 0 và lim v_n = 0, v_n > 0 với mọi n  thì $\lim \frac{u_n}{v_n}=+\infty$.

• lim u_n = +∞ ⇔ lim (–u_n) = –∞.

2. Giới hạn của hàm số

2.1. Giới hạn hữu hạn của hàm số tại một điểm

a) Định nghĩa

Cho khoảng K chứa điểm x₀ và hàm số f(x) xác định trên K hoặc trên K\{x₀}. Hàm số f(x) có giới hạn là số L khi x dần tới x₀ nếu với dãy số (x_n) bất kì, x_n ∈ K\{x₀} và x_n → x₀ thì f(x_n) → L.

Kí hiệu 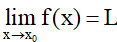 hay f(x) → L khi x → x₀.

Nhận xét: $\underset{x\to x_0}{\lim }x=x_0$; $\underset{x\to x_0}{\lim }c=c$, với c là hằng số.

Chú ý: Hàm số f(x) có thể không xác định tại x = x₀ nhưng vẫn tồn tại giới hạn của hàm số đó khi x dần tới x₀.

b) Phép toán trên giới hạn hữu hạn của hàm số

c) Giới hạn một phía

• Cho hàm số y = f(x) xác định trên khoảng (a; x₀).

Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x dần tới  x₀ nếu với dãy số (x_n) bất kì, a < x_n < x₀ và x_n → x₀, ta có f(x_n) → L.

Kí hiệu .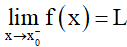

• Cho hàm số y = f(x) xác định trên khoảng (x₀; b).

Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x dần tới x₀ nếu với dãy số (x_n) bất kì, x₀ < x_n < b và x_n → x₀, ta có f(x_n) → L.

Kí hiệu .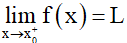

• .

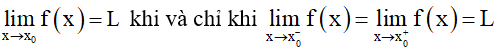
2.2. Giới hạn hữu hạn của hàm số tại vô cực

– Cho hàm số y = f(x) xác định trên khoảng (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới dương vô cực nếu với dãy số (x_n) bất kì, x_n > a và x_n → +∞, ta có f(x_n) → L.

Kí hiệu 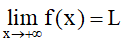 hay f(x) → L khi x → +∞.

– Cho hàm số y = f(x) xác định trên khoảng (–∞; a).

Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới âm vô cực nếu với dãy số (x_n) bất kì, x_n < a và x_n → –∞, ta có f(x_n) → L.

Kí hiệu 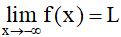 hay f(x) → L khi x → –∞.

Chú ý:

+ Với c, k là các hằng số và k nguyên dương, ta luôn có:

$\underset{x\to +\infty }{\lim }c=c;\underset{x\to -\infty }{\lim }c=c;\underset{x\to +\infty }{\lim }\frac{c}{x^k}=0;\underset{x\to -\infty }{\lim }\frac{c}{x^k}=0.$

+ Các phép toán trên giới hạn hữu hạn của hàm số khi x → x₀ vẫn còn đúng khi x → +∞ hoặc x → –∞.

2.3. Giới hạn vô cực (một phía) của hàm số tại một điểm

– Cho hàm số y = f(x) xác định trên khoảng (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là +∞ khi x → a⁺ nếu với dãy số (x_n) bất kì, x_n > a và x_n → a, ta có f(x_n) → +∞.

Kí hiệu 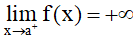 hay f(x) → +∞ khi x → a⁺.

– Các trường hợp 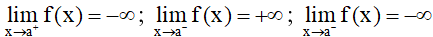 được định nghĩa tương tự.

Chú ý: Ta có các giới hạn cơ bản sau:

$\underset{x\to a^{+}}{\lim }\frac{1}{x-a}=+\infty ;\underset{x\to a^{-}}{\lim }\frac{1}{x-a}=-\infty$.

2.4. Giới hạn vô cực của hàm số tại vô cực

– Cho hàm số y = f(x) xác định trên khoảng (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là  +∞ khi x dần tới dương vô cực nếu với dãy số (x_n) bất kì, x_n > a và x_n → +∞, ta có f(x_n) → +∞.

Kí hiệu 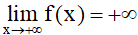 hay f(x) →+∞ khi x →  +∞.

– Các trường hợp 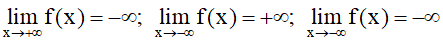 được định nghĩa tương tự.

Chú ý: Ta có ba giới hạn cơ bản sau:

• $\underset{x\to +\infty }{\lim }{x}^k=+\infty$ với k là số nguyên dương.

• $\underset{x\to -\infty }{\lim }{x}^k=+\infty$ k là số nguyên dương chẵn.

• $\underset{x\to -\infty }{\lim }{x}^k=-\infty$ k là số nguyên dương lẻ.

3. Hàm số liên tục

3.1. Khái niệm

a) Hàm số liên tục tại một điểm

Cho hàm số y = f(x) xác định trên khoảng (a; b) và x₀ ∈ (a; b). Hàm số y = f(x) được gọi là liên tục tại x₀ nếu .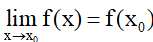

Nhận xét: Hàm số y = f(x) không liên tục tại x₀ được gọi là gián đoạn tại x₀.

b) Hàm số liên tục trên một khoảng hoặc một đoạn

– Hàm số y = f(x) được gọi là liên tục trên khoảng (a; b) nếu hàm số liên tục tại mọi điểm thuộc khoảng đó.

– Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu hàm số liên tục trên khoảng (a; b) và .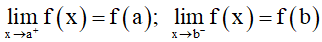

Chú ý: Khái niệm hàm số liên tục trên các tập hợp có dạng (a; b], [a; b), (a; +∞), [a; +∞), (–∞; a), (–∞; a], (–∞;+∞) được định nghĩa tương tự.

Nhận xét: Đồ thị hàm số liên tục trên một khoảng là “đường liền” trên khoảng đó.

3.2. Một số định lí cơ bản

a) Tính liên tục của một số hàm số sơ cấp cơ bản

– Các hàm đa thức và hai hàm số lượng giác y = sinx, y = cosx liên tục trên ℝ.

– Các hàm phân thức hữu tỉ và hai hàm số lượng giác y = tanx, y = cotx liên tục trên từng khoảng xác định của chúng.

– Hàm căn thức $y=\sqrt{x}$ liên tục trên nửa khoảng [0; +∞).

b) Tính liên tục của tổng, hiệu, tích, thương của hai hàm số liên tục

Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x₀. Khi đó:

– Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x) . g(x) liên tục tại x₀;

– Hàm số 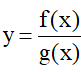 liên tục tại x₀ nếu g(x₀) ≠ 0.

Bài tập tổng hợp Toán 11 Chương 3

Bài 1. Tính các giới hạn sau:

a) $\lim \frac{3}{5n-2}$;

b) $\lim \frac{-4n+6}{2n}$;

c) $\lim \frac{4^n+{6.2}^n}{{3.4}^n}$;

d) $\lim \frac{5+\frac{-3}{n^2}}{4^n}$.

Hướng dẫn giải

Bài 2. Cho $u_n=\frac{1}{n^3}+2$ và $v_n=1-\frac{1}{n}$. Tính các giới hạn:

lim (u_n + v_n); lim(u_n – v_n); lim(u_n.v_n);  $\lim \frac{u_n}{v_n}$.

Hướng dẫn giải

Khi đó:

• lim (u_n + v_n) = lim u_n + lim v_n = 2 + 1 = 3.

• lim (u_n – v_n) = lim u_n – lim v_n = 2 – 1 = 1.

• lim (u_n . v_n) = lim u_n . lim v_n = 2 . 1 = 2

• $\lim \frac{u_n}{v_n}=\frac{\lim u_n}{\lim v_n}=\frac{2}{1}=2$.

Bài 3. Tính tổng của cấp số nhân lùi vô hạn biết u₁ = 1, công bội $q=\frac{2}{3}$.

Hướng dẫn giải

Tổng của cấp số nhân lùi vô hạn với u₁ = 1, công bội $q=\frac{2}{3}$ là:

  $S=u_1+u_{1}q+\mathrm{...}+u_1{q}^{n-1}+\mathrm{...}=\frac{1}{1-\frac{2}{3}}=3$.

Vậy S = 3.

Bài 4. Cho f(x) =1 – x và g(x) = 2x³. Tính các giới hạn sau:

Hướng dẫn giải

Bài 5. Tìm giới hạn của các hàm số sau:

Hướng dẫn giải

Bài 6. Dùng định nghĩa xét tính liên tục của hàm số f(x) = x³ + 2x – 1 tại x₀ = –1.

Hướng dẫn giải

Vậy hàm số đã cho liên tục tại x₀ = –1.

Bài 7. Xét tính liên tục của các hàm số sau trên tập xác định của hàm số đó:

a) f(x) = x + sinx;

Hướng dẫn giải

a) Hàm số f(x) có tập xác định là ℝ.

Hai hàm số x và sinx liên tục trên ℝ nên hàm số f(x) = x + sinx liên tục trên ℝ.

b) Hàm số 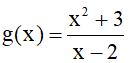 có tập xác định là ℝ\{2}.

Do đó hàm số 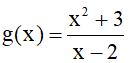 liên tục trên mỗi khoảng (–∞; 2) và (2; +∞).

c) Hàm số h(x) có tập xác định là ℝ.

Vì tử thức cosx liên tục ℝ và mẫu thức x² + 1 ≠ 0 liên tục trên ℝ.

Vậy h(x) liên tục trên ℝ.

Bài 8. Xét tính liêm tục của hàm số 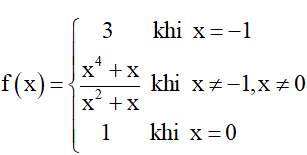  trên tập xác định của nó.

Hướng dẫn giải

Hàm số có TXĐ: D = ℝ.

Hàm số liên tục trên mỗi khoảng (–∞; –1); (–1; 0)  và (0; +∞).

• Tại x = –1, ta có:

⇒ Hàm số f(x) liên tục tại x = –1.

• Tại x = 0, ta có:

⇒ Hàm số f(x) liên tục tại x = 0.

Vậy hàm số f(x) liên tục tại mọi điểm x ∈ ℝ.

Bài 9. Tìm giá trị của tham số m để hàm số 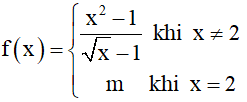 liên tục trên đoạn [0; 2].

Hướng dẫn giải

Hàm số xác định trên [0; 2] và liên tục trên [0; 2).

Khi đó để f(x) liên tục trên đoạn [0; 2] thì hàm số liên tục tại x = 2.

Tức là ta cần có: 

Ta có: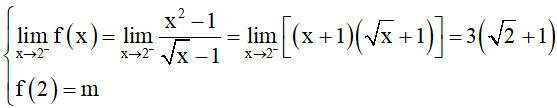     

Do đó (*) xảy ra khi và chỉ khi .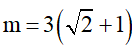

Xem thêm các bài tóm tắt lý thuyết Toán 11 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 2: Giới hạn của hàm số

Lý thuyết Bài 3: Hàm số liên tục

Lý thuyết Bài 1: Đường thẳng và mặt phẳng trong không gian

Lý thuyết Bài 2: Hai đường thẳng song song trong không gian

Lý thuyết Bài 3: Đường thẳng và mặt phẳng song song