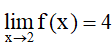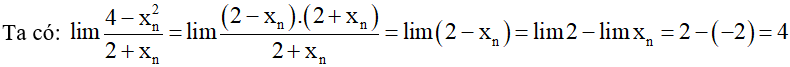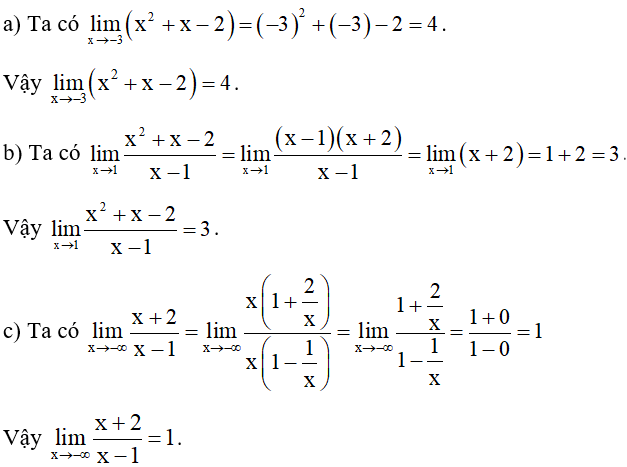Lý thuyết Toán 11 Bài 2: Giới hạn của hàm số (Cánh diều)

Lý thuyết Toán 11 Bài 2: Giới hạn của hàm số

1. Giới hạn hữu hạn của hàm số tại một điểm

1.1. Định nghĩa

Cho khoảng K chứa điểm x₀ và hàm số f(x) xác định trên K hoặc trên K\{x₀}. Hàm số f(x) có giới hạn là số L khi x dần tới x₀ nếu với dãy số (x_n) bất kì, x_n ∈ K\{x₀} và x_n → x₀ thì f(x_n) → L.

Kí hiệu 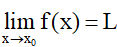 hay f(x) → L khi x → x₀.

Nhận xét: $\underset{x\to x_0}{\lim }x=x_0$; $\underset{x\to x_0}{\lim }c=c$, với c là hằng số.

Chú ý: Hàm số f(x) có thể không xác định tại x = x₀ nhưng vẫn tồn tại giới hạn của hàm số đó khi x dần tới x₀.

Ví dụ 1. Xét hàm số 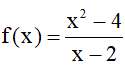 (x ≠ 2). Chứng minh rằng 

Hướng dẫn giải

Giả sử (x_n) là dãy bất kì, thỏa mãn x_n ≠ 2 và lim x_n = 2.

.

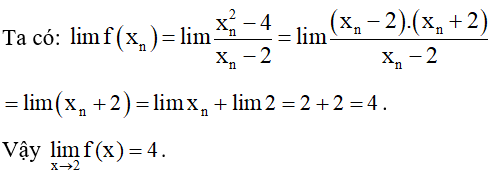
1.2. Phép toán trên giới hạn hữu hạn của hàm số

.

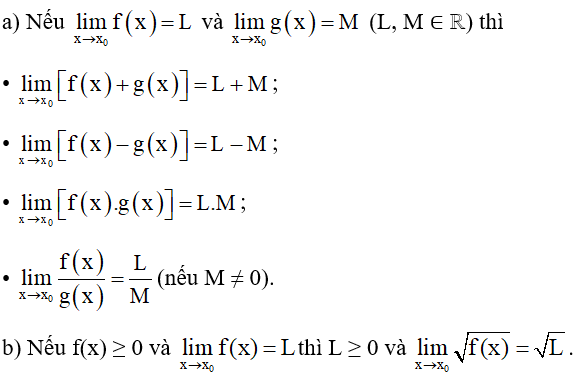
Ví dụ 2. Tìm

a) ;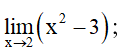

b) $\underset{x\to 0}{\lim }\frac{x+3}{x-4}$.

Hướng dẫn giải

.

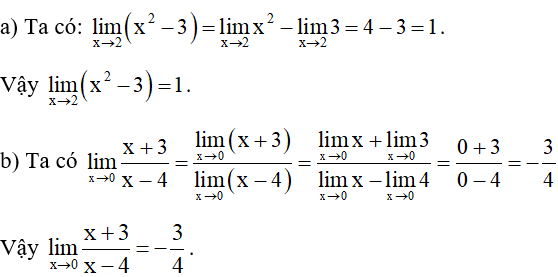
1.3. Giới hạn một phía

• Cho hàm số y = f(x) xác định trên khoảng (a; x₀).

Số L được gọi là giới hạn bên trái của hàm số y = f(x) khi x dần tới  x₀ nếu với dãy số (x_n) bất kì, a < x_n < x₀ và x_n → x₀, ta có f(x_n) → L.

Kí hiệu .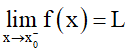

• Cho hàm số y = f(x) xác định trên khoảng (x₀; b).

Số L được gọi là giới hạn bên phải của hàm số y = f(x) khi x dần tới x₀ nếu với dãy số (x_n) bất kì, x₀ < x_n < b và x_n → x₀, ta có f(x_n) → L.

Kí hiệu .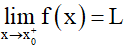

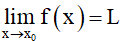
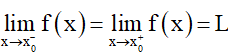
•  khi và chỉ khi .

Ví dụ 3.

.

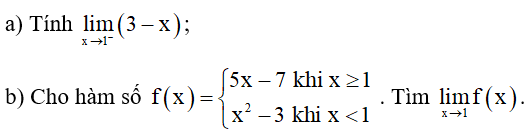
Hướng dẫn giải

.

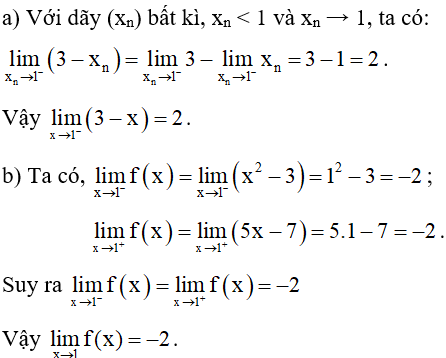
2. Giới hạn hữu hạn của hàm số tại vô cực

– Cho hàm số y = f(x) xác định trên khoảng (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới dương vô cực nếu với dãy số (x_n) bất kì, x_n > a và x_n → +∞, ta có f(x_n) → L.

Kí hiệu 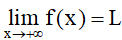 hay f(x) → L khi x → +∞.

– Cho hàm số y = f(x) xác định trên khoảng (–∞; a).

Ta nói hàm số y = f(x) có giới hạn là số L khi x dần tới âm vô cực nếu với dãy số (x_n) bất kì, x_n < a và x_n → –∞, ta có f(x_n) → L.

Kí hiệu 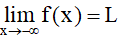 hay f(x) → L khi x → –∞.

Chú ý:

+ Với c, k là các hằng số và k nguyên dương, ta luôn có:

$\underset{x\to +\infty }{\lim }c=c;\underset{x\to -\infty }{\lim }c=c;\underset{x\to +\infty }{\lim }\frac{c}{x^k}=0;\underset{x\to -\infty }{\lim }\frac{c}{x^k}=0.$

+ Các phép toán trên giới hạn hữu hạn của hàm số khi x → x₀ vẫn còn đúng khi x → +∞ hoặc x → –∞.

Ví dụ 4. Tìm $\underset{x\to +\infty }{\lim }c=c;\underset{x\to -\infty }{\lim }c=c;\underset{x\to +\infty }{\lim }\frac{c}{x^k}=0;\underset{x\to -\infty }{\lim }\frac{c}{x^k}=0.$.

Hướng dẫn giải

.

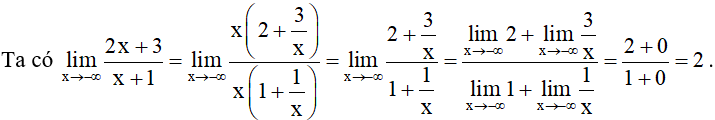
3. Giới hạn vô cực (một phía) của hàm số tại một điểm

– Cho hàm số y = f(x) xác định trên khoảng (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là +∞ khi x → a⁺ nếu với dãy số (x_n) bất kì, x_n > a và x_n → a, ta có f(x_n) → +∞.

Kí hiệu 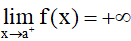 hay f(x) → +∞ khi x → a⁺.

– Các trường hợp 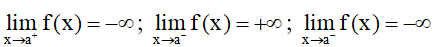;  được định nghĩa tương tự.

Chú ý: Ta có các giới hạn cơ bản sau:

$\underset{x\to a^{+}}{\lim }\frac{1}{x-a}=+\infty ;\underset{x\to a^{-}}{\lim }\frac{1}{x-a}=-\infty$.

Ví dụ 5. Tính $\underset{x\to 3^{-}}{\lim }\frac{1}{x-3}$.

Hướng dẫn giải

Ta có $\underset{x\to 3^{-}}{\lim }\frac{1}{x-3}$.

Vậy $\underset{x\to 3^{-}}{\lim }\frac{1}{x-3}=-\infty$.

4. Giới hạn vô cực của hàm số tại vô cực

– Cho hàm số y = f(x) xác định trên khoảng (a; +∞).

Ta nói hàm số y = f(x) có giới hạn là  +∞ khi x dần tới dương vô cực nếu với dãy số (x_n) bất kì, x_n > a và x_n → +∞, ta có f(x_n) → +∞.

Kí hiệu 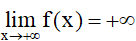 hay f(x) →+∞ khi x →  +∞.

– Các trường hợp 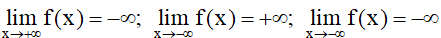 được định nghĩa tương tự.

Chú ý: Ta có ba giới hạn cơ bản sau:

• $\underset{x\to +\infty }{\lim }{x}^k=+\infty$ với k là số nguyên dương.

• $\underset{x\to -\infty }{\lim }{x}^k=+\infty$ k là số nguyên dương chẵn.

• $\underset{x\to -\infty }{\lim }{x}^k=-\infty$ k là số nguyên dương lẻ.

Ví dụ 6. $\underset{x\to +\infty }{\lim }{x}^5=+\infty$; $\underset{x\to -\infty }{\lim }{x}^5=-\infty$.

Bài tập Giới hạn của hàm số

Bài 1. Cho f(x) =1 – x và g(x) = 2x³. Tính các giới hạn sau:

.

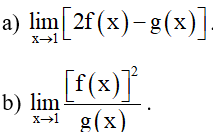
Hướng dẫn giải

.

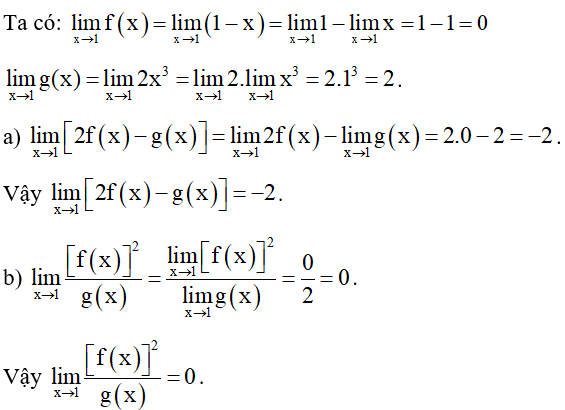
Bài 2. Sử dụng định nghĩa tìm giới hạn của hàm số:

a) $\underset{x\to 1}{\lim }{x}^3$;

b) $\underset{x\to -2}{\lim }\frac{4-x^2}{2+x}$.

Hướng dẫn giải

a) Giả sử (x_n) là một dãy bất kì và x_n → 1 khi n → +∞.

Khi đó $\mathrm{l}{\text{imx}}_n^3=1^3=1$.

Vậy $\underset{x\to 1}{\lim }{x}^3=1$.

b) Giả sử (x_n) là một dãy bất kì thỏa mãn x_n ≠ –2 và x_n → –2 khi n → +∞.

Vậy $\underset{x\to -2}{\lim }\frac{4-x^2}{2+x}=4$.

Bài 3. Tìm giới hạn của các hàm số sau:

a) ;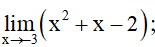

b) $\underset{x\to 1}{\lim }\frac{x^2+x-2}{x-1}$;

c) $\underset{x\to -\infty }{\lim }\frac{x+2}{x-1}$

Hướng dẫn giải

Xem thêm các bài tóm tắt lý thuyết Toán 11 Cánh diều hay, chi tiết khác:

Tổng hợp lý thuyết Toán 11 Chương 2

Lý thuyết Bài 1: Giới hạn của dãy số

Lý thuyết Bài 3: Hàm số liên tục

Tổng hợp lý thuyết Toán 11 Chương 3

Lý thuyết Bài 1: Đường thẳng và mặt phẳng trong không gian