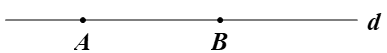Lý thuyết Toán 11 Bài 1: Đường thẳng và mặt phẳng trong không gian
1. Khái niệm mở đầu
Điểm, đường thẳng, mặt phẳng là ba đối tượng cơ bản của hình học không gian. Từ ba đối tượng cơ bản đó và những quan hệ cơ bản giữa chúng, ta tạo nên những vật thể khác nhau (như: hình chóp, hình nón,...) và xây dựng nên hình học không gian để nghiên cứu tính chất của những hình như vậy.
1.1. Mặt phẳng
Nhận xét: Mặt sân vận động cho ta hình ảnh một phần của mặt phẳng trong không gian.
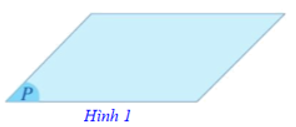
Người ta thường biểu diễn một mặt phẳng bằng một hình bình hành và dùng các chữ cái đặt trong dấu ngoặc đơn ( ) để đặt tên cho mặt phẳng ấy.
Ví dụ 1. Mặt phẳng (P) (Hình 1), mặt phẳng (Q), mặt phẳng (α), mặt phẳng (β),...
Trong thực tiễn có nhiều ví dụ minh họa cho mặt phẳng. Chẳng hạn: tấm gương phẳng, mặt bàn, bảng treo tường (Hình 2), bức tường, mặt ghế, tấm bìa carton,... cho ta hình ảnh một phần mặt phẳng trong không gian.
1.2. Điểm thuộc mặt phẳng
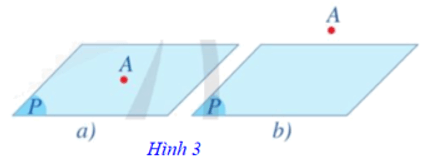
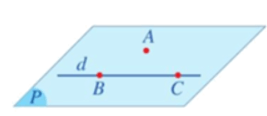
Nhận xét: Với mỗi điểm A và mặt phẳng (P), chỉ xảy ra một trong hai khả năng sau:
⦁ Điểm A thuộc mặt phẳng (P), ta kí hiệu A ∈ (P) (Hình 3a). Ta còn nói “điểm A nằm trong (hay nằm trên) mặt phẳng (P)”; “mặt phẳng (P) đi qua điểm A”;
⦁ Điểm A không thuộc mặt phẳng (P) hay A nằm ngoài (P), ta kí hiệu A ∉ (P) (Hình 3b).
1.3. Hình biểu diễn của một hình trong không gian
a) Khái niệm
Quy ước: Hình được vẽ trong mặt phẳng để giúp ta hình dung được về một hình trong không gian gọi là hình biểu diễn của hình không gian đó.
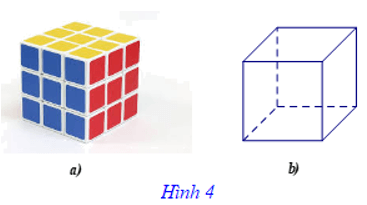
Ví dụ 2. Để hình dung được khối rubik ở Hình 4a), ta vẽ trên mặt phẳng như Hình 4b) minh họa khối rubik đó. Hình 4b) gọi là hình biểu diễn của khối rubik.
b) Quy tắc vẽ hình biểu diễn của một hình trong không gian
Để việc vẽ hình biểu diễn của một hình trong không gian được thuận lợi và thống nhất, ta quy ước như sau:
(1) Đường thẳng được biểu diễn bởi đường thẳng. Đoạn thẳng được biểu diễn bởi đoạn thẳng;
(2) Hai đường thẳng song song (hoặc cắt nhau) được biểu diễn bởi hai đường thẳng song song (hoặc cắt nhau);
(3) Hình biểu diễn giữ nguyên tính liên thuộc giữa điểm với đường thẳng hoặc với đoạn thẳng;
(4) Những đường nhìn thấy được vẽ bằng nét liền, những đường không nhìn thấy được vẽ bằng nét đứt.
Chú ý: Các quy tắc khác sẽ được đề cập sau.
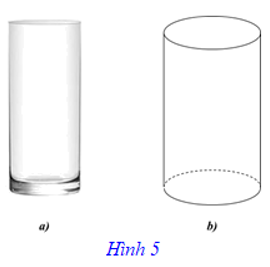
Ví dụ 3. Hình biểu diễn của chiếc ly thủy tinh ở Hình 5a) có thể được vẽ như Hình 5b).
2. Các tính chất thừa nhận của hình học không gian
Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
Tức là, có duy nhất một đường thẳng d đi qua hai điểm A, B phân biệt.
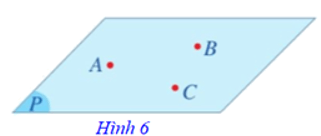
Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
Như vậy, mặt phẳng hoàn toàn xác định khi biết ba điểm A, B, C không thẳng hàng. Mặt phẳng đó được kí hiệu là mp(ABC) hay đơn giản là (ABC) (Hình 6).
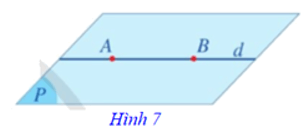
Tính chất 3: Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó.
Như vậy, nếu một đường thẳng d đi qua hai điểm phân biệt A, B của mặt phẳng (P) thì mọi điểm của đường thẳng d đều nằm trong mặt phẳng (P). Khi đó, ta nói d nằm trong (P), hoặc (P) chứa d, hoặc (P) đi qua d, kí hiệu d ⊂ (P) hay (P) ⊃ d (Hình 7).
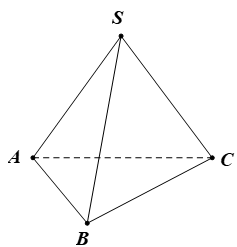
Tính chất 4: Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.
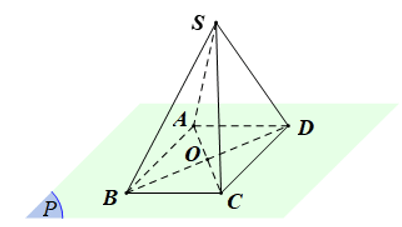
Ví dụ 4. Ở hình bên dưới, điểm S không nằm trên mặt phẳng (ABC) hay bốn điểm S, A, B, C không cùng nằm trên một mặt phẳng.
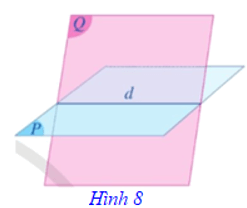
Tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
Nếu hai mặt phẳng phân biệt (P) và (Q) có điểm chung thì chúng có một đường thẳng chung duy nhất d chứa tất cả các điểm chung của hai mặt phẳng đó. Đường thẳng d đó gọi là giao tuyến của hai mặt phẳng (P) và (Q), kí hiệu d = (P) ∩ (Q) (Hình 8).
Ví dụ 5. Trong mặt phẳng (P), cho hình thoi ABCD, ngoài mặt phẳng (P), cho một điểm S. Hãy xác định:
a) Giao tuyến của hai mặt phẳng (SAB) và (SBC).
b) Giao điểm của mặt phẳng (SBD) và đường thẳng AC.
Hướng dẫn giải
a) Ta có S thuộc mặt phẳng (SAB) và S cũng thuộc mặt phẳng (SBC).
Suy ra S nằm trên giao tuyến của hai mặt phẳng (SAB) và (SBC).
Chứng minh tương tự, ta được B nằm trên giao tuyến của hai mặt phẳng (SAB) và (SBC).
Vậy đường thẳng SB là giao tuyến của hai mặt phẳng (SAB) và (SBC).
b) Gọi O là giao điểm của hai đường chéo AC và BD.
Ta có O nằm trên đường thẳng BD.
Mà đường thẳng BD nằm trong mặt phẳng (SBD).
Do đó O thuộc mặt phẳng (SBD).
Mà O cũng thuộc đường thẳng AC.
Vậy O là giao điểm của mặt phẳng (SBD) và đường thẳng AC.
Nhận xét:
⦁ Có thể xác định giao tuyến của hai mặt phẳng bằng cách đi tìm hai điểm chung của chúng. Đường thẳng đi qua hai điểm chung đó là giao tuyến cần tìm.
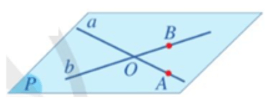
⦁ Để tìm giao điểm của đường thẳng a và mặt phẳng (P) (với giả thiết a cắt (P)), ta có thể làm như sau: Chọn một đường thẳng b thích hợp trong mặt phẳng (P) và tìm giao điểm M của hai đường thẳng a và b. Khi đó, M là giao điểm cần tìm.
Tính chất 6: Trên mỗi mặt phẳng của không gian, các kết quả đã biết của hình học phẳng đều đúng.
Ví dụ 6. Trên mặt phẳng (P) trong không gian, cho đường thẳng a và b.
Khi đó các định lí, tính chất đã học như định lí Thalès, vị trí tương đối giữa hai đường thẳng a và b, góc giữa hai đường thẳng a và b,... đều đúng.
3. Một số cách xác định mặt phẳng
Định lí 1: Cho điểm A không thuộc đường thẳng d. Khi đó, qua điểm A và đường thẳng d có một và chỉ một mặt phẳng, kí hiệu mp(A, d) hoặc (A, d).
Định lí 2: Cho hai đường thẳng a và b cắt nhau. Khi đó, qua a và b có một và chỉ một mặt phẳng, kí hiệu mp(a, b).
Nhận xét: Từ Tính chất 2 và hai định lí trên, ta thấy mặt phẳng hoàn toàn được xác định theo một trong ba cách sau:
⦁ Đi qua ba điểm không thẳng hàng;
⦁ Đi qua một đường thẳng và một điểm nằm ngoài đường thẳng đó;
⦁ Đi qua hai đường thẳng cắt nhau.
Ví dụ 7.
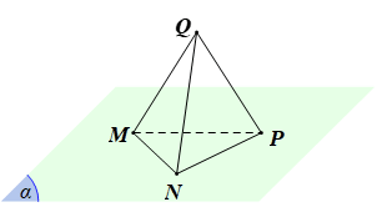
+ Trong mặt phẳng (α), cho tam giác MNP. Tam giác MNP xác định một phần của mặt phẳng (MNP) ≡ (α).
+ Gọi Q là một điểm nằm ngoài mặt phẳng (α). Khi đó đường thẳng MN và điểm Q xác định mặt phẳng (MNQ).
Tương tự, ta có thể xác định được các mặt phẳng (MPQ), (NPQ).
+ Hai đường thẳng MN và PQ không xác định một mặt phẳng vì hai đường thẳng MN và PQ không cắt nhau.
4. Hình chóp và hình tứ diện
4.1. Hình chóp
Quy ước: Từ nay, khi nói đến “tam giác”, ta có thể hiểu là hình gồm ba cạnh của nó hoặc là hình gồm ba cạnh và các điểm nằm trong tam giác đó. Đối với đa giác cũng như thế.
Trong mặt phẳng (P), cho đa giác A1A2...An (n ≥ 3). Lấy điểm S nằm ngoài (P). Nối S với các đỉnh A1, A2, ..., An ta được n tam giác: SA1A2, SA2A3, ..., SAnA1. Hình gồm đa giác A1A2...An và n tam giác SA1A2, SA2A3, ..., SAnA1 gọi là hình chóp, kí hiệu S.A1A2...An.
Chú ý:
⦁ Trong hình chóp S.A1A2...An, ta có:
– Điểm S gọi là đỉnh;
– Đa giác A1A2...An gọi là mặt đáy;
– Các cạnh của mặt đáy gọi là cạnh đáy;
– Các đoạn thẳng SA1, SA2, ..., SAn gọi là các cạnh bên;
– Các tam giác SA1A2, SA2A3, ..., SAnA1 gọi là các mặt bên.
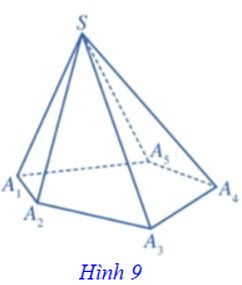
⦁ Nếu đáy của hình chóp là một tam giác, tứ giác, ngũ giác,... thì hình chóp tương ứng gọi là hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác,... Hình 9 minh họa cho hình chóp ngũ giác S.A1A2A3A4A5.
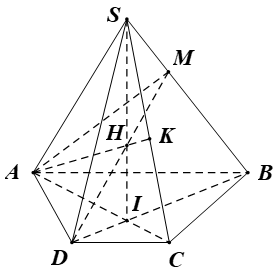
Ví dụ 8. Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi I là giao điểm của AC và BD. Trên cạnh SB lấy điểm M bất kì (M ≠ S, M ≠ B).
a) Xác định giao tuyến của hai mặt phẳng (ADM) và (SAC).
b) Xác định giao điểm của đường thẳng SC và mặt phẳng (ADM).
c) Xác định giao tuyến của hai mặt phẳng (ADM) và (SBC).
Hướng dẫn giải
a) Trong (SBD): gọi H là giao điểm của DM và SI.
Mà DM ⊂ (ADM) và SI ⊂ (SAC).
Suy ra H cùng thuộc hai mặt phẳng (ADM) và (SAC).
Mà A cùng thuộc hai mặt phẳng (ADM) và (SAC).
Vậy AH là giao tuyến của hai mặt phẳng (ADM) và (SAC).
b) Trong (SAC): gọi K là giao điểm của AH và SC.
Mà AH ⊂ (ADM). Do đó K ∈ (ADM).
Vậy K là giao điểm của đường thẳng SC và mặt phẳng (ADM).
c) Ta có K ∈ SC, mà SC ⊂ (SBC).
Do đó K ∈ (SBC).
Suy ra K cùng thuộc hai mặt phẳng (ADM) và (SBC) (1)
Lại có M ∈ SB, mà SB ⊂ (SBC), do đó M ∈ (SBC).
Suy ra M cùng thuộc hai mặt phẳng (ADM) và (SBC) (2)
Từ (1), (2), ta thu được MK là giao tuyến của hai mặt phẳng (ADM) và (SBC).
4.2. Hình tứ diện
Cho bốn điểm A, B, C, D không cùng nằm trong một mặt phẳng. Hình gồm bốn tam giác ABC, ACD, ABD và BCD gọi là hình tứ diện (hay ngắn gọn là tứ diện), kí hiệu là ABCD.
Chú ý:
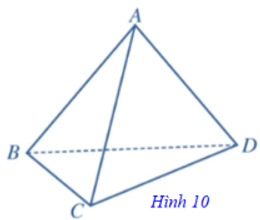
⦁ Trong hình tứ diện ABCD (Hình 10), ta có:
– Các điểm A, B, C, D gọi là các đỉnh.
– Các đoạn thẳng AB, BC, CD, DA, CA, BD gọi là các cạnh. Hai cạnh không có điểm chung gọi là hai cạnh đối diện.
– Các tam giác ABC, ACD, ABD, BCD gọi là các mặt.
– Đỉnh không nằm trên một mặt gọi là đỉnh đối diện với mặt đó.
⦁ Hình tứ diện có các mặt là tam giác đều gọi là hình tứ diện đều.
⦁ Mỗi hình chóp tam giác là một hình tứ diện. Ngược lại, nếu ta quy định rõ đỉnh và mặt đáy trong một hình tứ diện thì hình tứ diện đó trở thành hình chóp tam giác.
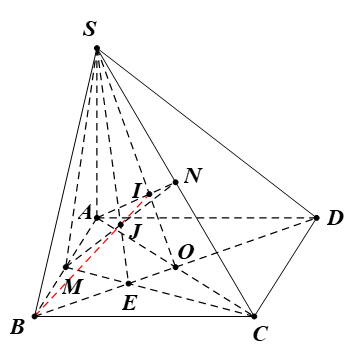
Ví dụ 9. Cho tứ diện ABCD. Trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N, trên cạnh BC lấy điểm O sao cho MN không song song với BD và MO không song song với AC.
a) Xác định H, K lần lượt là giao điểm của các đường thẳng AC, CD với mặt phẳng (OMN).
b) Gọi G là giao điểm của MN và OK. Chứng minh rằng ba điểm B, D, G thẳng hàng.
Hướng dẫn giải
a) Trong (ABC): gọi H là giao điểm của MO và AC.
Mà MO ⊂ (OMN) nên H là giao điểm của AC và (OMN).
Vì H ∈ MO nên H ∈ (OMN).
Trong (ACD): gọi K là giao điểm của NH và CD.
Mà NH ⊂ (OMN).
Do đó K là giao điểm của CD và (OMN).
b) Ta có G là giao điểm của MN và OK.
Mà MN ⊂ (ABD) và OK ⊂ (BCD).
Suy ra G thuộc giao tuyến của hai mặt phẳng (ABD) và (BCD) (1)
Lại có B, D đều cùng thuộc hai mặt phẳng (ABD) và (BCD).
Suy ra BD là giao tuyến của hai mặt phẳng (ABD) và (BCD) (2)
Từ (1), (2), ta thu được ba điểm B, D, G thẳng hàng.
Nhận xét: Để chứng minh ba điểm thẳng hàng, ta có thể chỉ ra ba điểm đó cùng thuộc hai mặt phẳng phân biệt.
Bài tập Đường thẳng và mặt phẳng trong không gian
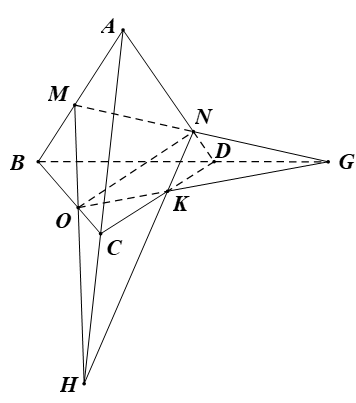
Bài 1. Cho hình chóp S.ABCD. Gọi M, N lần lượt là trung điểm của các cạnh SC và SD. Gọi O là giao điểm AC và BD.
a) Tìm giao tuyến của các cặp mặt phẳng (SAC) và (SBD); (SAB) và (SCD).
b) Tìm giao điểm P của đường thẳng BN với mặt phẳng (SAC).
c) Gọi Q và R lần lượt là trung điểm của SA và SB. Chứng minh rằng bốn điểm M, N, Q, R cùng nằm trên một mặt phẳng.
Hướng dẫn giải
a) Trong (ABCD): O là giao điểm AC và BD.
Mà AC ⊂ (SAC) và BD ⊂ (SBD).
Do đó O cùng thuộc hai mặt phẳng (SAC) và (SBD).
Mà S cùng thuộc hai mặt phẳng (SAC) và (SBD).
Vậy SO là giao tuyến của hai mặt phẳng (SAC) và (SBD).
Trong (ABCD): gọi E là giao điểm của AB và CD.
Mà AB ⊂ (SAB) và CD ⊂ (SCD).
Do đó E cùng thuộc hai mặt phẳng (SAB) và (SCD).
Mà S cùng thuộc hai mặt phẳng (SAB) và (SCD).
Vậy SE là giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Trong (SBD): gọi P là giao điểm của SO và BN.
Mà SO ⊂ (SAC).
Vậy P là giao điểm của đường thẳng BN và mặt phẳng (SAC).
c) Trong (SCD): gọi T là giao điểm của MN và SE.
Tam giác SCD có M, N lần lượt là trung điểm của SC, SD.
Suy ra MN là đường trung bình của tam giác SCD.
Do đó MN // CD.
Xét tam giác SDE, có: MT // DE (chứng minh trên) và N là trung điểm SD.
Suy ra T là trung điểm SE.
Tương tự, ta có QR là đường trung bình của tam giác SAB.
Do đó QR // AB.
Xét tam giác SAE, có: QT // AE (chứng minh trên) và Q là trung điểm SA.
Suy ra QR đi qua trung điểm T của SE.
Như vậy, bốn điểm M, N, Q, R cùng thuộc một mặt phẳng, mặt phẳng này là (QNT)
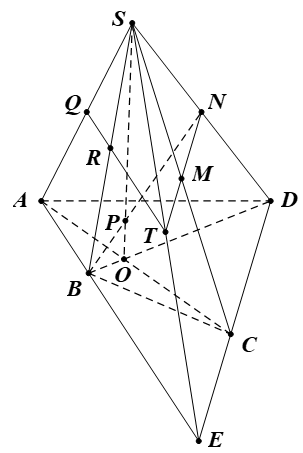
Bài 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của đoạn AB và SC.
a) Xác định giao điểm I của đường thẳng AN và mặt phẳng (SBD).
b) Xác định giao điểm J của đường thẳng MN và mặt phẳng (SBD).
c) Chứng minh ba điểm I, J, B thẳng hàng.
Hướng dẫn giải
a) Trong (ABCD): gọi O là giao điểm của AC và BD.
Trong (SAC): gọi I là giao điểm của AN và SO.
Mà SO ⊂ (SBD).
Vậy I là giao điểm của đường thẳng AN và mặt phẳng (SBD).
b) Trong (ABCD): gọi E là giao điểm của MC và BD.
Trong (SMC): gọi J là giao điểm của MN và SE.
Mà SE ⊂ (SBD).
Vậy J là giao điểm của đường thẳng MN và mặt phẳng (SBD).
c) Ta có ba điểm I, J, B lần lượt nằm trên các đường thẳng AN, MN, AM.
Suy ra ba điểm I, J, B đều thuộc mặt phẳng (AMN).
Mà ba điểm I, J, B đều thuộc (SBD).
Do đó ba điểm I, J, B đều nằm trên đường giao tuyến của hai mặt phẳng (AMN) và (SBD).
Vậy ba điểm I, J, B thẳng hàng.
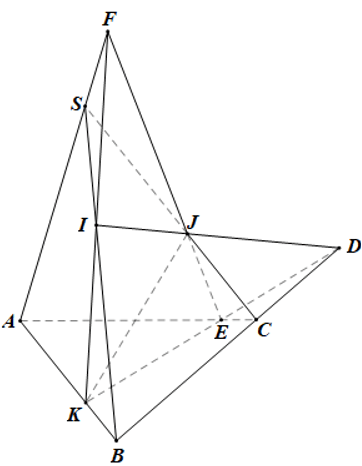
Bài 3. Cho tứ diện S.ABC. Gọi I, J, K lần lượt là các điểm nằm trên các cạnh SB, SC và AB sao cho IJ không song song với BC, IK không song song với SA.
a) Tìm giao điểm D của mặt phẳng (IJK) và đường thẳng BC.
b) Gọi E là giao điểm của DK và AC. Chứng minh ba đường thẳng SA, KI, EJ đồng quy.
Hướng dẫn giải
a) Trong (SBC): gọi D là giao điểm của IJ và BC.
Mà IJ ⊂ (IJK).
Vậy D là giao điểm của mặt phẳng (IJK) và đường thẳng BC.
b) Trong (ABC): gọi F là giao điểm của IK và SA.
Mà IK ⊂ (IJK) và SA ⊂ (SAC).
Suy ra F đều thuộc hai mặt phẳng (IJK) và (SAC) (1)
Lại có E là giao điểm của DK và AC.
Mà DK ⊂ (IJK) và AC ⊂ (SAC).
Suy ra E đều thuộc hai mặt phẳng (IJK) và (SAC) (2)
Mặt khác, J là giao điểm của ID và SC.
Mà ID ⊂ (IJK) và SC ⊂ (SAC).
Suy ra J đều thuộc hai mặt phẳng (IJK) và (SAC) (3)
Từ (1), (2), (3), suy ra ba điểm F, E, J đều nằm trên đường giao tuyến của hai mặt phẳng (IJK) và (SAC).
Khi đó ba điểm F, E, J thẳng hàng.
Vậy ba đường thẳng SA, KI, EJ đồng quy tại F.
Xem thêm các bài tóm tắt lý thuyết Toán 11 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 3: Hàm số liên tục
Tổng hợp lý thuyết Toán 11 Chương 3
Lý thuyết Bài 2: Hai đường thẳng song song trong không gian
Lý thuyết Bài 3: Đường thẳng và mặt phẳng song song
Lý thuyết Bài 4: Hai mặt phẳng song song