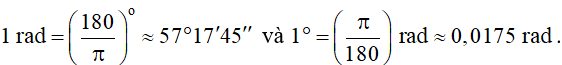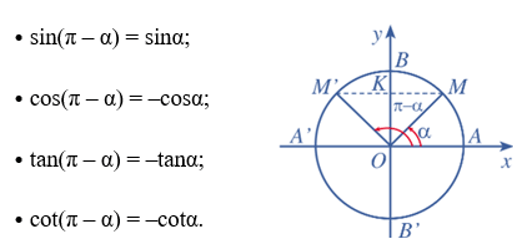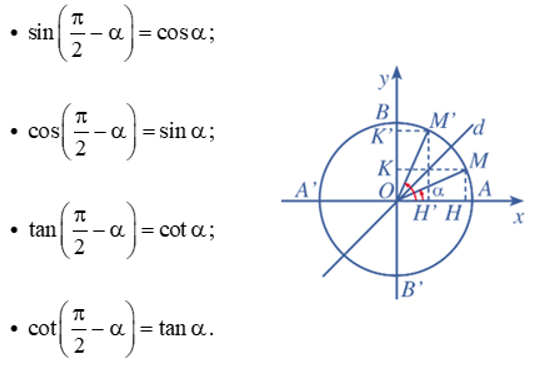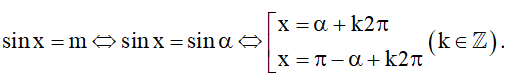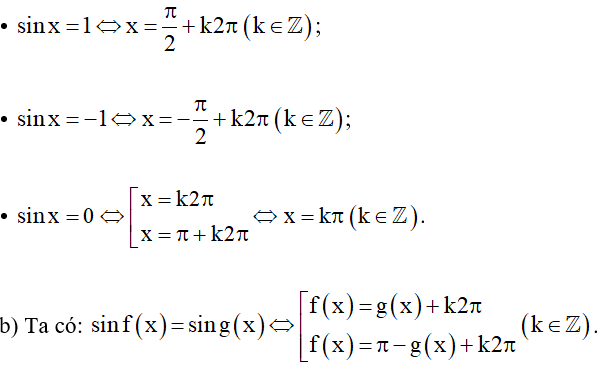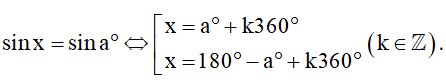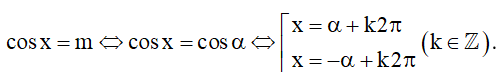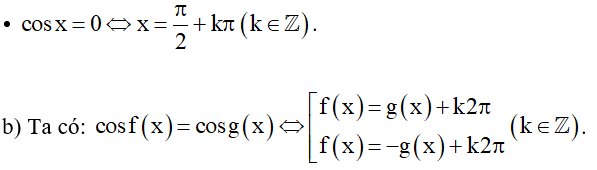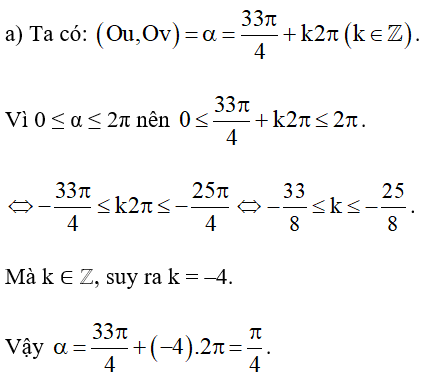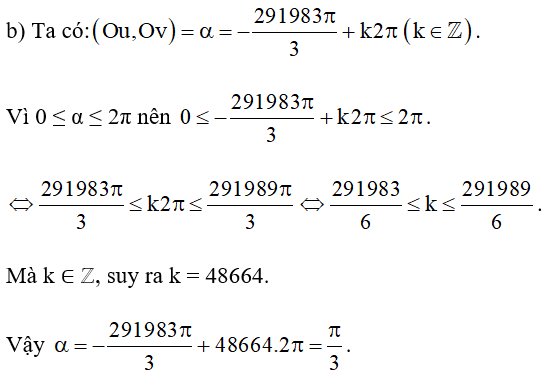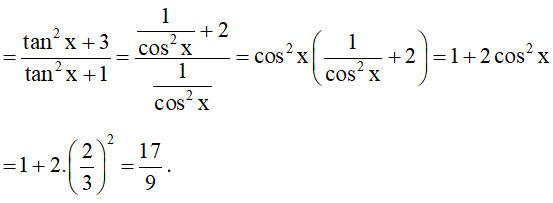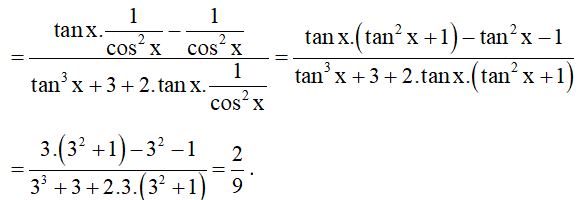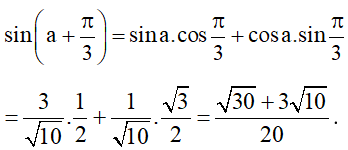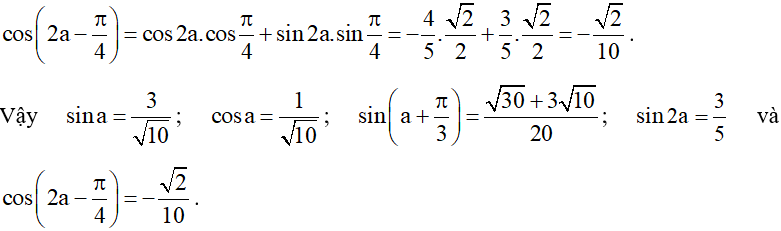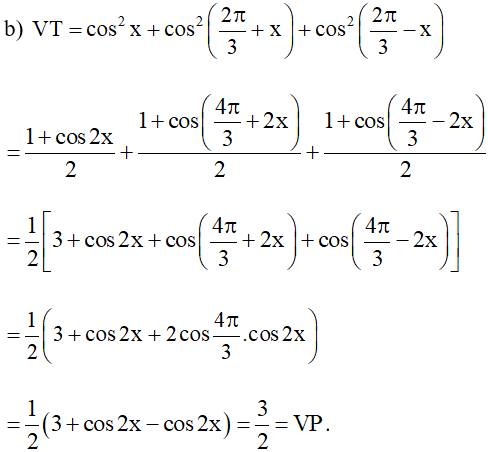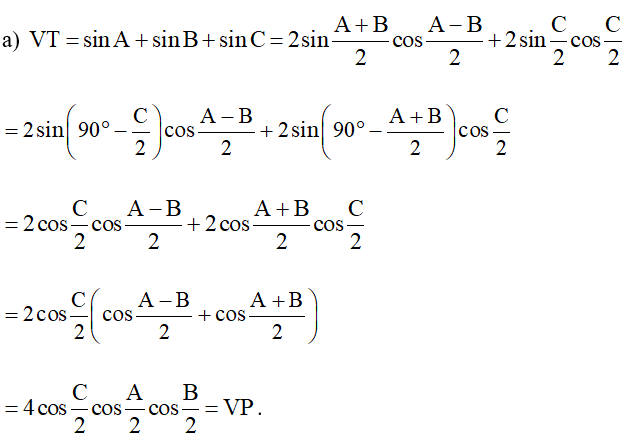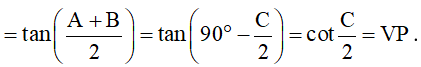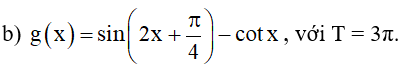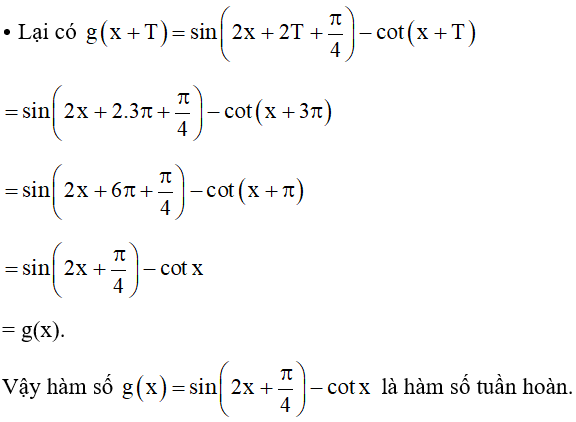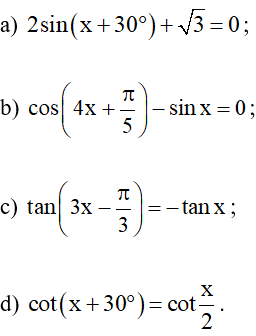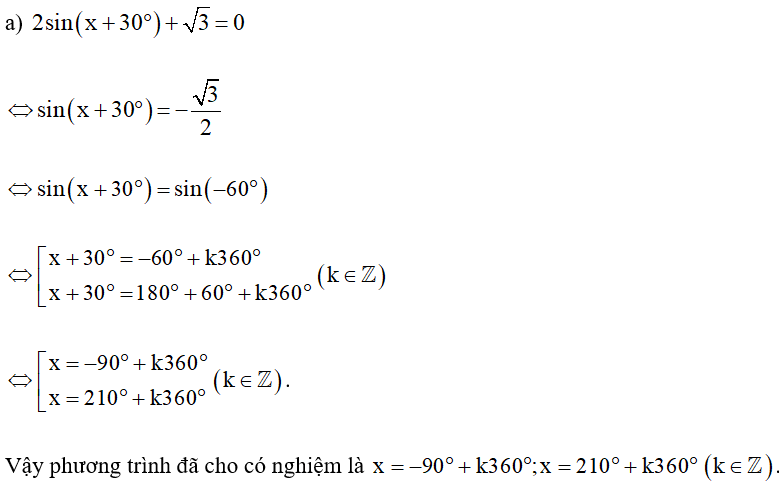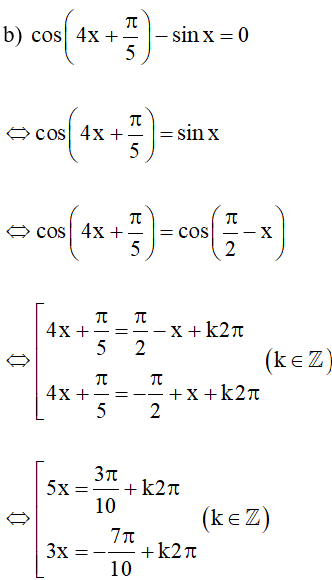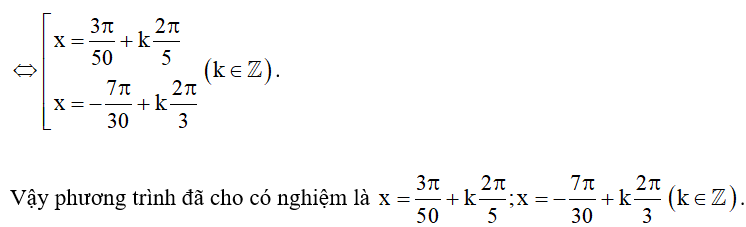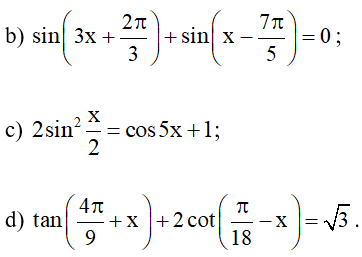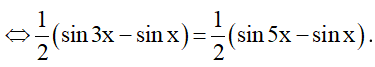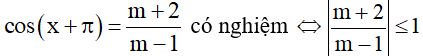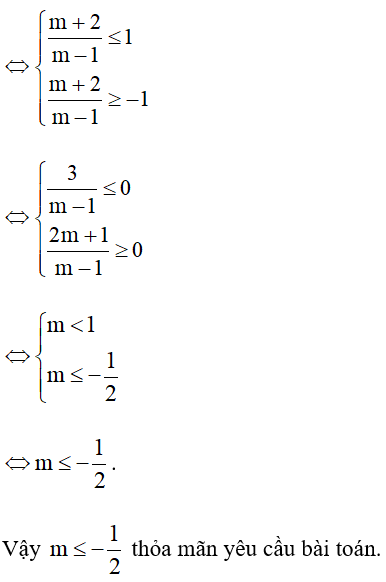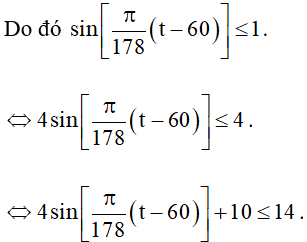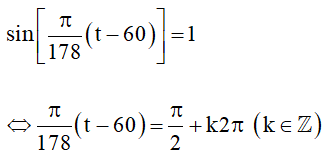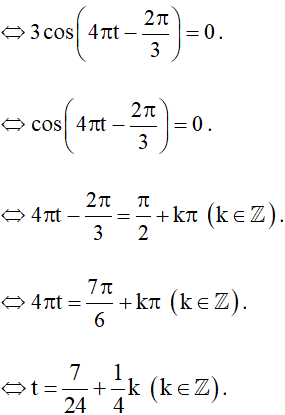Lý thuyết Toán 11 Chương 1: Hàm số lượng giác và phương trình lượng giác (Cánh diều)

Lý thuyết Toán 11 Chương 1: Hàm số lượng giác và phương trình lượng giác

I. Góc lượng giác. Giá trị lượng giác của góc lượng giác

1. Góc lượng giác

1.1. Góc hình học và số đo của chúng

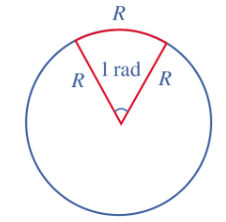
– Góc (còn được gọi là góc hình học) là hình gồm hai tia chung gốc. Mỗi góc có một số đo, đơn vị đo góc (hình học) là độ. Số đo của một góc (hình học) không vượt quá 180°.

– Một đơn vị khác được sử dụng nhiều khi đo góc là radian (đọc là ra-đi-an), viết tắt là rad.

Nhận xét:

Chú ý: Người ta thường không viết chữ radian hay rad sau số đo của góc.

Chẳng hạn, $\frac{\pi }{2}$ rad cũng được viết là $\frac{\pi }{2}$.

1.2. Góc lượng giác và số đo của chúng

a) Khái niệm

Quy ước chọn chiều dương là chiều ngược chiều quay của kim đồng hồ và chiều cùng chiều quay của kim đồng hồ gọi là chiều âm.

Góc lượng giác: Cho hai tia Ou, Ov. Nếu tia Om quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ tia Ou đến trùng với tia Ov thì ta nói: Tia Om quét một góc lượng giác với tia đầu Ou và tia cuối Ov, kí hiệu là (Ou, Ov).

Nhận xét:

– Khi tia Om quay góc a° thì góc lượng giác mà tia đó quét nên có số đo a° (hay $\frac{\pi a}{180}$ rad).

– Mỗi một góc lượng giác đều có một số đo, đơn vị đo góc lượng giác là độ hoặc radian.

– Nếu góc lượng giác (Ou, Ov) có số đo bằng α thì ta kí hiệu là sđ(Ou, Ov) = α hoặc (Ou, Ov) = α.

– Mỗi góc lượng giác gốc O được xác định bởi tia đầu Ou, tia cuối Ov và số đo của góc đó.

b) Tính chất

Định lí: Nếu một góc lượng giác có số đo α° (hay α radian) thì mọi góc lượng giác có cùng tia đầu, tia cuối với góc lượng giác đó có số đo dạng: α° + k360° (hay α + k2π), với k là số nguyên, mỗi góc ứng với một giá trị của k.

Định lí (hệ thức Chasles): Với ba tia tùy ý Ou, Ov, Ow, ta có:

(Ou, Ov) + (Ov, Ow) = (Ou, Ow) + k2π (k ∈ ℤ).

2. Giá trị lượng giác của góc lượng giác

2.1. Đường tròn lượng giác

Trong mặt phẳng tọa độ Oxy, ta quy ước: Chiều ngược chiều quay của kim đồng hồ là chiều dương và chiều quay của kim đồng hồ là chiều âm. Như vậy, mặt phẳng tọa độ Oxy đã được định hướng.

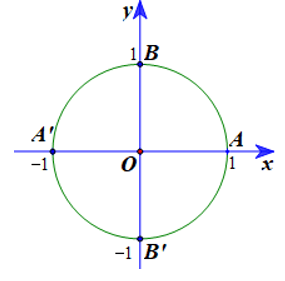
Đường tròn lượng giác: Trong mặt phẳng tọa độ đã được định hướng Oxy, lấy điểm A(1; 0). Đường tròn tâm O bán kính OA = 1 được gọi là đường tròn lượng giác (hay đường tròn đơn vị) gốc A.

Chú ý: Các điểm B(0; 1), A’(–1; 0), B’(0; –1) nằm trên đường tròn lượng giác.

2.2. Giá trị lượng giác của góc lượng giác

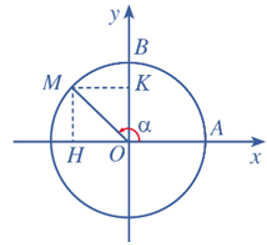
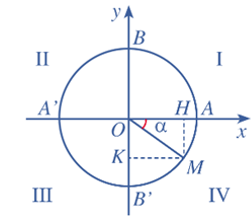
– Trong trường hợp tổng quát, với mỗi góc lượng giác α, lấy điểm M trên đường tròn lượng giác sao cho (OA, OM) = α (Hình vẽ).

Gọi tọa độ của điểm M trong hệ tọa độ Oxy là (x; y).

⦁ Hoành độ x của điểm M gọi là côsin của góc lượng giác α và kí hiệu cosα, cosα = x.

⦁ Tung độ y của điểm M gọi là sin của góc lượng giác α và kí hiệu sinα, sinα = y.

⦁ Nếu cosα ≠ 0 thì tỉ số $\frac{\sin \alpha }{\cos \alpha }$ gọi là tang của góc lượng giác α và kí hiệu tanα, $\tan \alpha =\frac{\sin \alpha }{\cos \alpha }$.

⦁ Nếu sinα ≠ 0 thì tỉ số $\frac{\cos \alpha }{\sin \alpha }$ gọi là côtang của góc lượng giác α và kí hiệu là cotα, $\cot \alpha =\frac{\cos \alpha }{\sin \alpha }$.

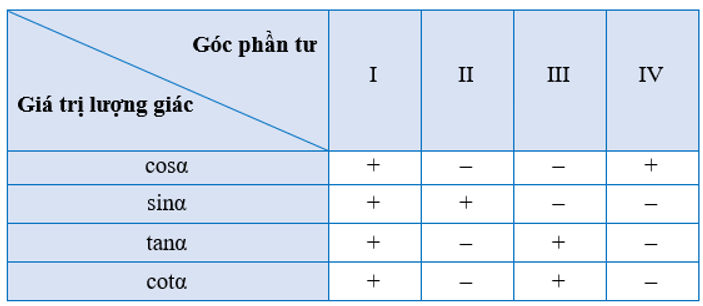
– Dấu của các giá trị lượng giác của góc α = (OA, OM) phụ thuộc vào vị trí điểm M trên đường tròn lượng giác ­(Hình vẽ).

Bảng xác định dấu của các giá trị lượng giác như sau:

Các công thức lượng giác cơ bản:

⦁ cos²α + sin²α = 1, với mọi α;

⦁ $\tan \alpha =\frac{1}{\cot \alpha }$, với cosα ≠ 0, sinα ≠ 0;

⦁ $1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }$, với cosα ≠ 0;

⦁ $1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }$, với sinα ≠ 0.

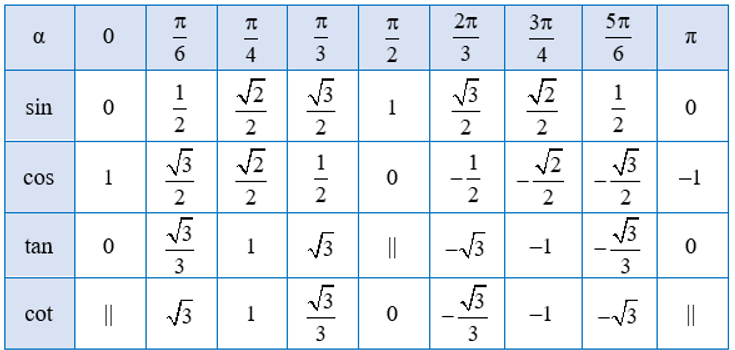
Bảng dưới đây nêu lên các giá trị lượng giác của một số góc đặc biệt:

2.3. Giá trị lượng giác của các góc có liên quan đặc biệt

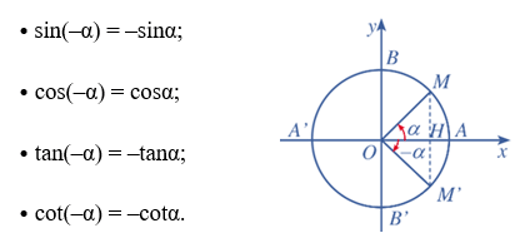
– Hai góc đối nhau (α và – α):

– Hai góc bù nhau (α và π – α):

– Hai góc phụ nhau (α và $\frac{\pi }{2}-\alpha$):

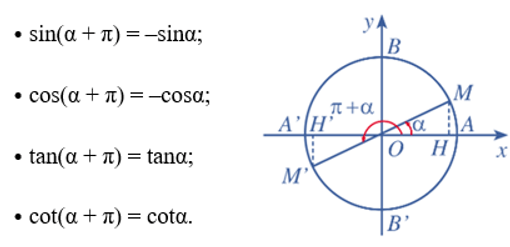
– Hai góc hơn kém nhau π (α và α + π):

2.4. Sử dụng máy tính cầm tay để tính giá trị lượng giác của một góc lượng giác

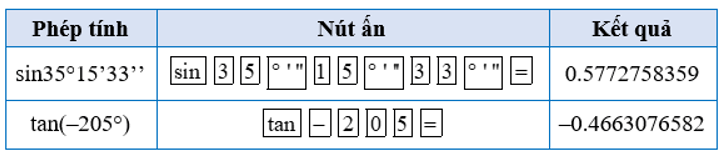
Ta có thể sử dụng máy tính cầm tay để tính giá trị lượng giác (đúng hoặc gần đúng) của một góc lượng giác khi biết số đo của góc đó. Cụ thể như sau:

⦁ Nếu đơn vị của góc lượng giác là độ (°), trước hết, ta chuyển máy tính sang chế độ “độ”.

⦁ Nếu đơn vị của góc lượng giác là radian (rad), trước hết, ta chuyển máy tính sang chế độ “radian”.

II. Các phép biến đổi lượng giác

1. Công thức cộng

⦁ sin(a + b) = sina.cosb + cosa.sinb;

⦁ sin(a – b) = sina.cosb – cosa.sinb.

⦁ cos(a + b) = cosa.cosb – sina.sinb;

⦁ cos(a – b) = cosa.cosb + sina.sinb.

.

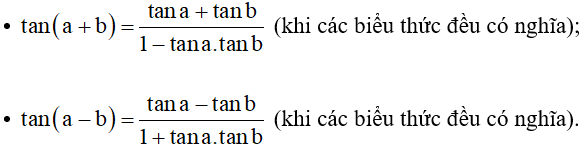
2. Công thức nhân đôi

⦁ sin2a = 2sina.cosa;

⦁ cos2a = cos²a – sin²a;

⦁ $\tan 2a=\frac{2\tan a}{1-{\tan }^{2}a}$ (khi các biểu thức đều có nghĩa).

Nhận xét:

⦁ cos2a = cos²a – sin²a = 2cos²a – 1 = 1 – 2sin²a;

⦁ ${\cos }^{2}a=\frac{1+\cos 2a}{2};{\sin }^{2}a=\frac{1-\cos 2a}{2}$ (thường gọi là công thức hạ bậc).

3. Công thức biến đổi tích thành tổng

.

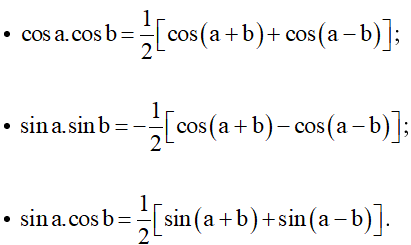
4. Công thức biến đổi tổng thành tích

⦁ $\cos u+\cos v=2.\cos \frac{u+v}{2}.\cos \frac{u-v}{2}$;

⦁$\cos u-\cos v=-2.\sin \frac{u+v}{2}.\sin \frac{u-v}{2}$;

⦁$\sin u+\sin v=2.\sin \frac{u+v}{2}.\cos \frac{u-v}{2}$;

⦁$\sin u-\sin v=2.\cos \frac{u+v}{2}.\sin \frac{u-v}{2}$.

III. Hàm số lượng giác và đồ thị

1. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

1.1. Hàm số chẵn, hàm số lẻ

Cho hàm số y = f(x) với tập xác định D.

⦁ Hàm số y = f(x) được gọi là hàm số chẵn nếu ∀x ∈ D thì –x ∈ D và f(–x) = f(x).

⦁ Hàm số y = f(x) được gọi là hàm số lẻ nếu ∀x ∈ D thì –x ∈ D và f(–x) = –f(x).

Chú ý:

⦁ Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.

⦁ Đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

1.2 Hàm số tuần hoàn

Cho hàm số y = f(x) với tập xác định D. Hàm số y = f(x) được gọi là tuần hoàn nếu tồn tại một số T khác 0 sao cho với mọi x ∈ D, ta có:

⦁ x + T ∈ D và x – T ∈ D;

⦁ f(x + T) = f(x).

Số T dương nhỏ nhất thỏa mãn các tính chất trên (nếu có) được gọi là chu kì của hàm số tuần hoàn đó.

Nhận xét: Cho hàm số tuần hoàn chu kì T. Từ đồ thị hàm số trên đoạn [a; a + T], ta dịch chuyển song song với trục hoành sang phải (hoặc sang trái) theo đoạn có độ dài T thì được đồ thị hàm số trên đoạn [a + T; a + 2T] (hoặc [a – T; a]).

2. Hàm số y = sinx

2.1. Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x với một số thực sinx được gọi là hàm số y = sinx.

Tập xác định của hàm số y = sinx là ℝ.

2.2. Đồ thị của hàm số y = sinx

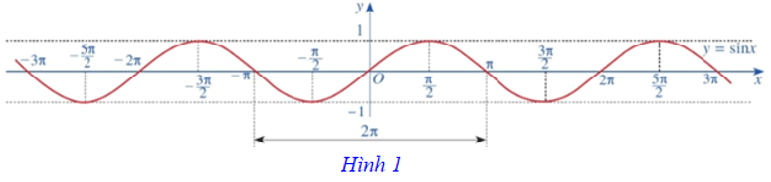
Ta có đồ thị của hàm số y = sinx trên ℝ được biểu diễn ở Hình 1:

2.3. Tính chất của hàm số y = sinx

Hàm số y = sinx có tập giá trị là [–1; 1] và có những tính chất sau:

⦁ Là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O;

⦁ Là hàm số tuần hoàn chu kì 2π;

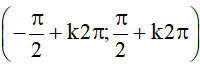
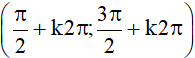
⦁ Là hàm số đồng biến trên mỗi khoảng , nghịch biến trên mỗi khoảng  với k ∈ ℤ.

Nhận xét: Dựa vào đồ thị của hàm số y = sinx (Hình 1), ta thấy sinx = 0 tại những giá trị x = kπ (k ∈ ℤ). Vì vậy, tập hợp các số thực x sao cho sinx ≠ 0 là E = ℝ \ {kπ | k ∈ ℤ}.

3. Hàm số y = cosx

3.1. Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x với một số thực cosx được gọi là hàm số y = cosx.

Tập xác định của hàm số y = cosx là ℝ.

3.2. Đồ thị của hàm số y = cosx

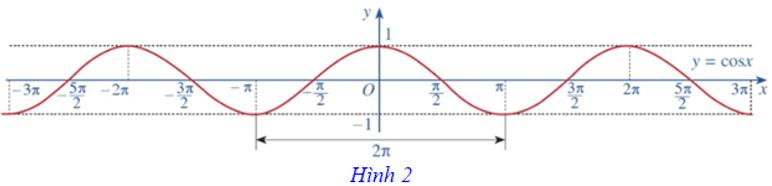
Ta có đồ thị của hàm số y = cosx trên ℝ được biểu diễn ở Hình 2.

3.3. Tính chất của hàm số y = cosx

Hàm số y = cosx có tập giá trị là [–1; 1] và có những tính chất sau:

⦁ Là hàm số chẵn, có đồ thị đối xứng qua trục tung;

⦁ Là hàm số tuần hoàn chu kì 2π;

⦁ Là hàm số đồng biến trên mỗi khoảng (–π + k2π; k2π), nghịch biến trên mỗi khoảng (k2π; π + k2π) với k ∈ ℤ.

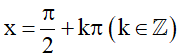
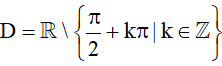
Nhận xét: Dựa vào đồ thị của hàm số y = cosx (Hình 2), ta thấy cosx = 0 tại những giá trị . Vì vậy, tập hợp các số thực x sao cho cosx ≠ 0 là .

4. Hàm số y = tanx

4.1. Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x ∈ D với một số thực tanx được gọi là hàm số y = tanx. Tập xác định của hàm số y = tanx là .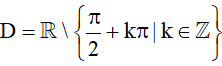

4.2. Đồ thị của hàm số y = tanx

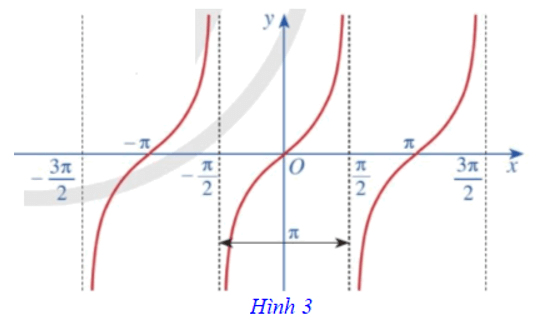
Ta có đồ thị hàm số y = tanx trên D được biểu diễn ở Hình 3.

4.3. Tính chất của hàm số y = tanx

Hàm số y = tanx có tập giá trị là ℝ và có những tính chất sau:

⦁ Là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O;

⦁ Là hàm số tuần hoàn chu kì π;

⦁ Là hàm số đồng biến trên mỗi khoảng 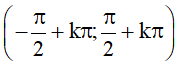 với k ∈ ℤ.

5. Hàm số y = cotx

3.5.1. Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x ∈ E với một số thực cotx được gọi là hàm số y = cotx. Tập xác định của hàm số y = cotx là E = ℝ \ {kπ | k ∈ ℤ}.

5.2. Đồ thị của hàm số y = cotx

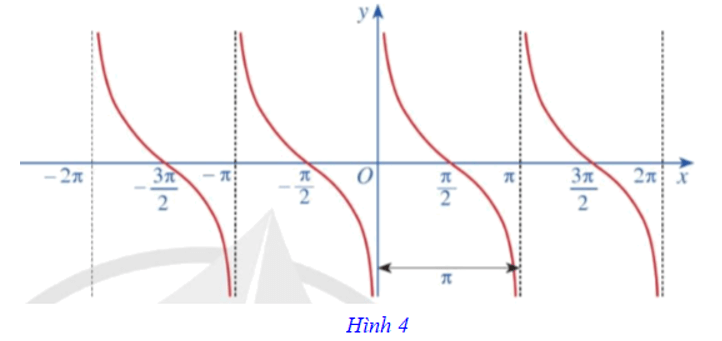
Ta có đồ thị hàm số y = cotx trên E được biểu diễn ở Hình 4.

5.3. Tính chất của hàm số y = cotx

Hàm số y = cotx có tập giá trị là ℝ và có những tính chất sau:

⦁ Là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O;

⦁ Là hàm số tuần hoàn chu kì π;

⦁ Là hàm số nghịch biến trên mỗi khoảng (kπ; π + kπ) với k ∈ ℤ.

IV. Phương trình lượng giác cơ bản

1. Phương trình tương đương

– Định nghĩa:

Hai phương trình (cùng ẩn) được gọi là tương đương nếu chúng có cùng tập nghiệm.

Nếu phương trình f₁(x) = g₁(x) tương đương với phương trình f₂(x) = g₂(x) thì ta viết f₁(x) = g₁(x) ⇔ f₂(x) = g₂(x).

Chú ý: Khi giải phương tình cần lưu ý tới điều kiện xác định của phương trình (hay gọi tắt là điều kiện của phương trình).

– Định lí sau đây nêu lên một số phép biến đổi tương đương thường sử dụng:

Nếu thực hiện các phép biến đổi sau đây trên một phương trình mà không làm thay đổi điều kiện của nó thì ta được một phương trình mới tương đương.

a) Cộng hay trừ hai vế với cùng một số hoặc cùng một biểu thức.

b) Nhân hoặc chia hai vế với cùng một số khác 0 hoặc với cùng một biểu thức luôn có giá trị khác 0.

2. Phương trình sinx = m

Trong trường hợp tổng quát, ta có thể giải phương trình sinx = m như sau:

⦁ Với |m| > 1, phương trình sinx = m vô nghiệm.

⦁ Với |m| ≤ 1, gọi α là số thực thuộc đoạn 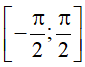 sao cho sinα = m. Khi đó, ta có:

Chú ý:

a) Ta có một số trường hợp đặc biệt sau của phương trình sinx = m:

c) Nếu x là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác x sao cho sinx = sina° như sau:

3. Phương trình cosx = m

Trong trường hợp tổng quát, ta có thể giải phương trình cosx = m như sau:

⦁ Với |m| > 1, phương trình cosx = m vô nghiệm.

⦁ Với |m| ≤ 1, gọi α là số thực thuộc đoạn [0; π] sao cho cosα = m. Khi đó, ta có:

Chú ý:

a) Ta có một số trường hợp đặc biệt sau của phương trình cosx = m:

⦁ cosx = 1 ⇔ x = k2π (k ∈ ℤ);

⦁ cosx = –1 ⇔ x = π + k2π (k ∈ ℤ);

c) Nếu x là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác x sao cho cosx = cosa° như sau: .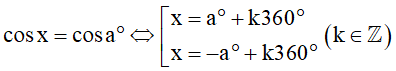

4. Phương trình tanx = m

Trong trường hợp tổng quát, ta có cách giải phương trình tanx = m như sau:

Gọi α là số thực thuộc khoảng 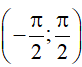 sao cho tanα = m. Khi đó với mọi m ∈ ℝ, ta có:

tanx = m ⇔ tanx = tanα ⇔ x = α + kπ (k ∈ ℤ).

Chú ý: Nếu x là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác x sao cho tanx = tana° như sau:

tanx = tana° ⇔ x = a° + k180° (k ∈ ℤ).

5. Phương trình cotx = m

Trong trường hợp tổng quát, ta có cách giải phương trình cotx = m như sau:

Gọi α là số thực thuộc khoảng (0; π) sao cho cotα = m. Khi đó với mọi m ∈ ℝ, ta có:

cotx = m ⇔ cotx = cotα ⇔ x = α + kπ (k ∈ ℤ).

Chú ý: Nếu x là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác x sao cho cotx = cota° như sau:

cotx = cota° ⇔ x = a° + k180° (k ∈ ℤ).

6. Giải phương trình lượng giác cơ bản bằng máy tính cầm tay

Có thể sử dụng máy tính cầm tay (MTCT) để giải các phương trình lượng giác cơ bản.

Chú ý: Để giải phương trình cotx = a (a ≠ 0) bằng MTCT, ta đưa về giải phương trình $\tan x=\frac{1}{a}$.

Ví dụ. Sử dụng MTCT để giải mỗi phương trình sau với kết quả là radian (làm tròn kết quả đến hàng phần nghìn):

a) $\sin x=\frac{1}{4}$;

b) cos2x = –0,7;

c) tanx = –2;

d) cotx = 5.

Hướng dẫn giải

Chuyển MTCT sang chế độ “radian”.

a) Bấm liên tiếp các phím sau trên MTCT: .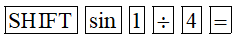

Ta được kết quả gần đúng (làm tròn đến hàng phần nghìn) là: 0,253.

Khi đó, ta có: .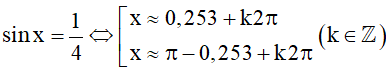

Vậy phương trình đã cho có nghiệm là 

b) Bấm liên tiếp các phím sau trên MTCT: .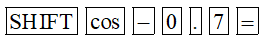

Ta được kết quả gần đúng (làm tròn đến hàng phần nghìn) là: 2,346.

Khi đó, ta có: cos2x = –0,7 ⇔ 2x ≈ ±2,346 + k2π (k ∈ ℤ).

⇔ x ≈ ±1,173 + kπ (k ∈ ℤ).

Vậy phương trình đã cho có nghiệm là: x ≈ ±1,173 + kπ (k ∈ ℤ).

c) Bấm liên tiếp các phím sau trên MTCT: .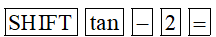

Ta được kết quả gần đúng (làm tròn đến hàng phần nghìn) là: –1,107.

Khi đó, ta có: tanx = –2 ⇔ x ≈ –1,107 + kπ (k ∈ ℤ).

Vậy phương trình đã cho có nghiệm là: x ≈ –1,107 + kπ (k ∈ ℤ).

d) $\cot x=5\iff \tan x=\frac{1}{5}$.

Bấm liên tiếp các phím sau trên MTCT: .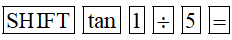

Ta được kết quả gần đúng (làm tròn đến hàng phần nghìn) là: 0,197.

Khi đó, ta có: .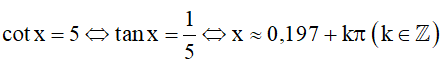

Vậy phương trình đã cho có nghiệm là: x ≈ 0,197 + kπ (k ∈ ℤ).

Bài tập tổng hợp Toán 11 Chương 1

Bài 1. Tìm số đo α của góc lượng giác (Ou, Ov) với 0 ≤ α ≤ 2π (0° ≤ α ≤ 360°), biết một góc lượng giác có cùng tia đầu, tia cuối với góc đó có số đo là:

a) $\frac{33\pi }{4}$;

b) $-\frac{291983\pi }{3}$;

c) 3270°.

Hướng dẫn giải

c) Ta có: (Ou,Ov) = α = 3270° + k.360° (k ∈ ℤ).

Vì 0° ≤ α ≤ 360° nên 0° ≤ 3270° + k.360° ≤  360°.

⇔ –3270° ≤ k.360° ≤  –2910°$\iff -\frac{109}{12}\le k\le -\frac{97}{12}$.

Mà k ∈ ℤ, suy ra k = –9.

Vậy α = 3270° + (–9).360° = 30°.

Bài 2.

a) Cho $\cos x=\frac{2}{3}$. Tính $A=\frac{\tan x+3\cot x}{\tan x+\cot x}$.

b) Cho $\sin x=-\frac{4}{5}$ và $\frac{3\pi }{2}<x<2\pi$. Tính $B=\frac{\sin x+3\cos x}{\tan x}$.

c) Cho tanx = 3. Tính $C=\frac{\sin x-\cos x}{{\sin }^{3}x+3{\cos }^{3}x+2\sin x}$.

Hướng dẫn giải

a) Ta có $A=\frac{\tan x+3\cot x}{\tan x+\cot x}=\frac{\tan x+3.\frac{1}{\tan x}}{\tan x+\frac{1}{\tan x}}$ (do cosx ≠ 0)

                 

b) Vì $\frac{3\pi }{2}<x<2\pi$ nên cosx > 0.

Ta có sin²x + cos²x = 1, suy ra .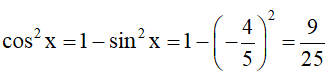

$\iff \cos x=\frac{3}{5}$ (do cosx > 0).

Suy ra $\tan x=\frac{\sin x}{\cos x}=-\frac{4}{5}:\frac{3}{5}=-\frac{4}{3}$.

Khi đó $B=\frac{\sin x+3\cos x}{\tan x}=\frac{-\frac{4}{5}+3.\frac{3}{5}}{-\frac{4}{3}}=-\frac{3}{4}$.

c) Do tanx = 3 nên cosx ≠ 0.

Chia cả tử và mẫu của C cho cos³x, ta được:

$C=\frac{\frac{\sin x}{{\cos }^{3}x}-\frac{\cos x}{{\cos }^{3}x}}{\frac{{\sin }^{3}x}{{\cos }^{3}x}+3+2.\frac{\sin x}{{\cos }^{3}x}}$

Bài 3. Cho $\cos 2a=-\frac{4}{5}$, với $\frac{\pi }{4}<a<\frac{\pi }{2}$. Tính sina, cosa, , sin2a, .

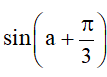
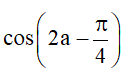
Hướng dẫn giải

Vì $\frac{\pi }{4}<a<\frac{\pi }{2}$ nên sina > 0, cosa > 0.

• Áp dụng công thức hạ bậc, ta được: ${\sin }^{2}a=\frac{1-\cos 2a}{2}=\frac{1+\frac{4}{5}}{2}=\frac{9}{10}$.

Suy ra $\sin a=\frac{3}{\sqrt{10}}$ (do sina > 0)

• Áp dụng công thức hạ bậc, ta được: ${\cos }^{2}a=\frac{1+\cos 2a}{2}=\frac{1-\frac{4}{5}}{2}=\frac{1}{10}$.

Suy ra $\cos a=\frac{1}{\sqrt{10}}$.

• Áp dụng công thức cộng đối với sin, ta được:

• Áp dụng công thức nhân đôi, ta được:

$\sin 2a=2\sin a\cos a=2.\frac{3}{\sqrt{10}}.\frac{1}{\sqrt{10}}=\frac{3}{5}$.

• Áp dụng công thức cộng đối với côsin, ta được:

Bài 4. Chứng minh rằng:

a) ${\cos }^{3}x.\sin x-{\sin }^{3}x.\cos x=\frac{1}{4}\sin 4x$;

Hướng dẫn giải

a) VT = cos³x.sinx – sin³x.cosx

= cosx.sinx.(cos²x – sin²x)

$=\frac{1}{2}\sin 2x.\cos 2x$$=\frac{1}{4}\sin 4x$ = VP.

Vậy ta có điều phải chứng minh.

Vậy ta có điều phải chứng minh.

Bài 5. Cho ∆ABC. Chứng minh rằng:

a) $\sin A+\sin B+\sin C=4\cos \frac{A}{2}\cos \frac{B}{2}\cos \frac{C}{2}$;

b) $\frac{\sin A+\sin B}{\cos A+\cos B}=\cot \frac{C}{2}$;

c) $\sin 2A+\sin 2B+\sin 2C=\frac{2S}{R^2}$, với R là bán kính đường tròn ngoại tiếp ∆ABC và S là diện tích ∆ABC.

Hướng dẫn giải

∆ABC, có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$, suy ra $\widehat{A}+\widehat{B}=180°-\widehat{C}$

Do đó $\frac{\widehat{A}+\widehat{B}}{2}=90°-\frac{\widehat{C}}{2}$.

Vậy ta có điều phải chứng minh.

b) $VT=\frac{\sin A+\sin B}{\cos A+\cos B}=\frac{2\sin \frac{A+B}{2}\cos \frac{A-B}{2}}{2\cos \frac{A+B}{2}\cos \frac{A-B}{2}}$

Vậy ta có điều phải chứng minh.

c) VT = sin2A + sin2B + sin2C

= 2sin(A + B).cos(A – B) + 2sinC.cosC

= 2sin(180° – C).cos(A – B) + 2sinC.cosC

= 2sinC.cos(A – B) + 2sinC.cosC

= 2sinC.[cos(A – B) + cosC]

= 2sinC.[cos(A – B) + cos(180° – A – B)]

= 2sinC.[cos(A – B) – cos(A + B)]

= –4sinC.sinA.sin(–B)

= 4sinA.sinB.sinC

$=4.\frac{a}{2R}.\frac{b}{2R}.\frac{c}{2R}=\frac{abc}{4R}.\frac{2}{R^2}=\frac{2S}{R^2}=VP$.

Vậy ta có điều phải chứng minh.

Bài 5. Xác định tham số m để:

a) Hàm số f(x) = 5m.sin4x + cos2x là hàm số chẵn.

b) Hàm số g(x) = (m – 1).tanx.cotx là hàm số lẻ.

Hướng dẫn giải

a) Hàm số f(x) có tập xác định là D = ℝ.

Ta có ∀x ∈ ℝ thì –x ∈ ℝ.

Để hàm số f(x) là hàm số chẵn thì f(–x) = f(x), ∀x ∈ ℝ.

⇔ 5m.sin(–4x) + cos(–2x) = 5m.sin4x + cos2x, ∀x ∈ ℝ.

⇔ –5m.sin4x + cos2x = 5m.sin4x + cos2x, ∀x ∈ ℝ.

⇔ 10m.sin4x = 0, ∀x ∈ ℝ.

⇔ m = 0.

Vậy m = 0 thỏa mãn yêu cầu bài toán.

b) Hàm số g(x) có tập xác định là .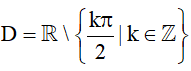

Ta có ∀x ∈ D thì –x ∈ D.

Để hàm số g(x) là hàm số lẻ thì f(–x) = –f(x), ∀x ∈ D.

⇔ (m – 1).tan(–x).cot(–x) = –(m – 1).tanx.cotx, ∀x ∈ D.

⇔ (m – 1).tanx.cotx = –(m – 1).tanx.cotx, ∀x ∈ D.

⇔ 2(m – 1).tanx.cotx = 0, ∀x ∈ D.

⇔ m – 1 = 0.

⇔ m = 1.

Vậy m = 1 thỏa mãn yêu cầu bài toán.

Bài 7. Chứng minh các hàm số sau là hàm số tuần hoàn:

a) f(x) = tan2x, với $T=\frac{3\pi }{2}$;

Hướng dẫn giải

a) Hàm số f(x) có tập xác định là .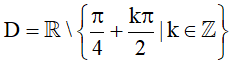

⦁ Ta có ∀x ∈ D thì $x+T=x+\frac{3\pi }{2}\in D$ và $x-T=x-\frac{3\pi }{2}\in D$.

⦁ Lại có .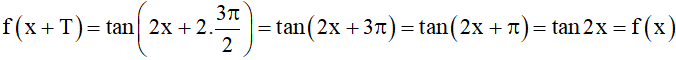

Vậy hàm số f(x) = tan2x là hàm số tuần hoàn.

b) Hàm số g(x) có tập xác định là E = ℝ \ {kπ | k ∈ ℤ}.

⦁ Ta có ∀x ∈ E thì x + T = x + 3π ∈ E và x – T = x – 3π ∈ E.

Bài 8. Giải các phương trình sau:

Hướng dẫn giải

⇔ x = –60° + k360° (k ∈ ℤ).

Vậy phương trình đã cho có nghiệm là x = –60° + k360° (k ∈ ℤ).

Bài 9. Giải các phương trình sau:

a) sinx.cos2x = sin2x.cos3x;

Hướng dẫn giải

a) sinx.cos2x = sin2x.cos3x.

⇔ sin3x – sinx = sin5x – sinx.

⇔ sin5x = sin3x.

c) $2{\sin }^2\frac{x}{2}=\cos 5x+1$.

$\iff \cos 5x+1-2{\sin }^2\frac{x}{2}=0$.

⇔ cos5x + cosx = 0.

⇔ 2cos3x.cos2x = 0.

Bài 10.

a) Cho phương trình $\sin \frac{x}{3}=m^2+9$, m là tham số. Với giá trị nào của m thì phương trình đã cho vô nghiệm?

b) Cho phương trình 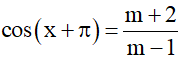, m là tham số. Với giá trị nào của m thì phương trình đã cho có nghiệm?

Hướng dẫn giải

a) TXĐ: D = ℝ.

Phương trình $\sin \frac{x}{3}=m^2+9$ vô nghiệm ⇔ |m² + 9| > 1.

⇔ m² + 9 > 1.

⇔ m² > –8, ∀m ∈ ℝ.

Vậy phương trình $\sin \frac{x}{3}=m^2+9$ vô nghiệm, ∀m ∈ ℝ.

b) TXĐ: D = ℝ.

Phương trình 

$\iff -1\le \frac{m+2}{m-1}\le 1$

Bài 11. Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t của năm 2017 (có 365 ngày) được cho bởi một hàm số 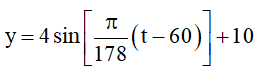, với t ∈ ℤ và 0 < t ≤ 365. Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?

Hướng dẫn giải

Ta có tập giá trị của hàm số y = sinx là [–1; 1].

Tức là, sinx ≤ 1.

⇔ y ≤ 14 (*)

Yêu cầu bài toán ⇔ Tìm t để y = 14, với 0 < t ≤ 365.

Ta có dấu “=” của (*) xảy ra khi và chỉ khi  (**)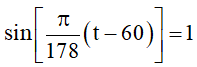

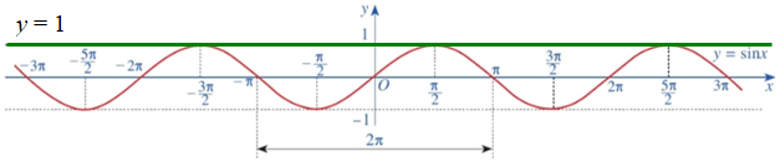
Cách 1: Dùng đồ thị

Quan sát hình vẽ, ta thấy đồ thị hàm số y = sinx cắt đường thẳng y = 1 tại $x=\frac{\pi }{2}+k2\pi$, với k ∈ ℤ.

Do đó (**) tương đương với: .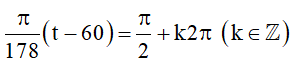

⇔ t – 60 = 89 + 356k (k ∈ ℤ).

⇔ t = 149 + 356k (k ∈ ℤ).

Cách 2: Giải phương trình

⇔ t – 60 = 89 + 356k (k ∈ ℤ).

⇔ t = 149 + 356k (k ∈ ℤ).

Vì 0 < t ≤ 365 nên 0 < 149 + 356k ≤ 365.

⇔ –149 < 356k ≤ 216.

$\iff -\frac{149}{356}<k\le \frac{54}{89}$.

Mà k ∈ ℤ nên k = 0.

Với k = 0, ta có: t = 149.

Vậy ngày 29 tháng 5 năm 2017 là ngày thành phố A có nhiều giờ có ánh sáng mặt trời nhất.

Bài 12. Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình 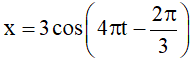, với t là thời gian tính bằng giây và x là quãng đường tính bằng cm. Hãy cho biết trong khoảng thời gian từ 0 đến 5 giây, vật đi qua vị trí cân bằng bao nhiêu lần?

Hướng dẫn giải

Yêu cầu bài toán ⇔ Tìm t sao cho x = 0, với 0 ≤ t ≤ 5.

Ta có x = 0.

Ta có 0 ≤ t ≤ 5.

$\iff 0\le \frac{7}{24}+\frac{1}{4}k\le 5$.

$\iff -\frac{7}{24}\le \frac{1}{4}k\le \frac{113}{24}$.

$\iff -\frac{7}{6}\le k\le \frac{113}{6}$.

Mà k ∈ ℤ nên k ∈ {–1; 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18}.

Có tất cả 20 giá trị k thỏa mãn.

Vậy trong khoảng thời gian từ 0 đến 5 giây, vật đi qua vị trí cân bằng 20 lần.

Xem thêm các bài tóm tắt lý thuyết Toán 11 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 3: Hàm số lượng giác và đồ thị

Lý thuyết Bài 4: Phương trình lượng giác cơ bản

Lý thuyết Bài 1: Dãy số

Lý thuyết Bài 2: Cấp số cộng

Lý thuyết Bài 3: Cấp số nhân