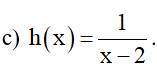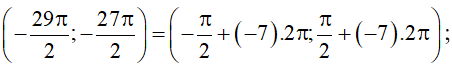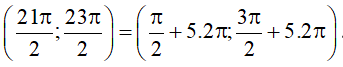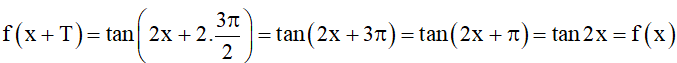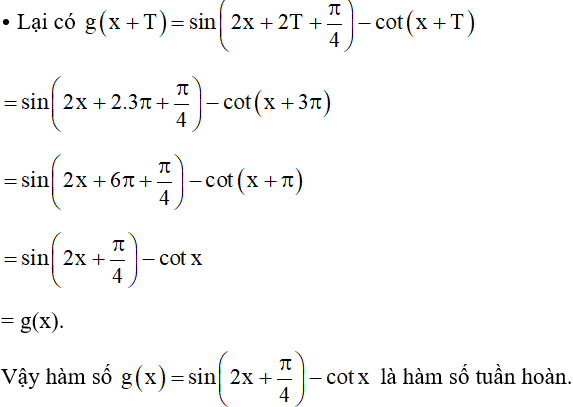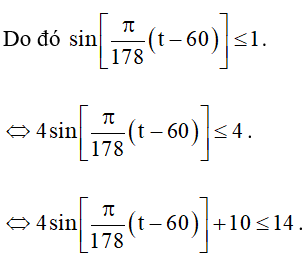Lý thuyết Toán 11 Bài 3: Hàm số lượng giác và đồ thị (Cánh diều)

Lý thuyết Toán 11 Bài 3: Hàm số lượng giác và đồ thị

1. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

1.1. Hàm số chẵn, hàm số lẻ

Cho hàm số y = f(x) với tập xác định D.

⦁ Hàm số y = f(x) được gọi là hàm số chẵn nếu ∀x ∈ D thì –x ∈ D và f(–x) = f(x).

⦁ Hàm số y = f(x) được gọi là hàm số lẻ nếu ∀x ∈ D thì –x ∈ D và f(–x) = –f(x).

Chú ý:

⦁ Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.

⦁ Đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

Ví dụ 1. Xét tính chẵn, lẻ của các hàm số sau, từ đó xác định đồ thị hàm số có nhận trục Oy làm trục đối xứng hay nhận gốc tọa độ làm tâm đối xứng hay không.

a) f(x) = –5x² + 2;

b) g(x) = 2x;

Hướng dẫn giải

a) Hàm số f(x) = –5x² + 2, có:

⦁ Tập xác định là D = ℝ;

⦁ ∀x ∈ ℝ thì –x ∈ ℝ và f(–x) = –5.(–x)² + 2 = –5x² + 2 = f(x).

Vậy hàm số f(x) = –5x² + 2 là hàm số chẵn và đồ thị hàm số nhận trục tung là trục đối xứng.

b) Hàm số g(x) = 2x, có:

⦁ Tập xác định là D = ℝ;

⦁ ∀x ∈ ℝ thì –x ∈ ℝ và g(–x) = 2.(–x) = –2x = –g(x).

Vậy hàm số g(x) = 2x là hàm số lẻ và đồ thị hàm số nhận gốc tọa độ O là tâm đối xứng.

c) Hàm số 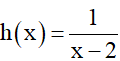, có tập xác định là D = ℝ \{2}.

Ta thấy x = –2 ∈ D nhưng x = 2 ∉ D.

Vậy hàm số 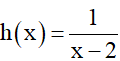 không chẵn không lẻ và không nhận trục Oy làm trục đối xứng, cũng không nhận gốc tọa độ O làm tâm đối xứng.

1.2 Hàm số tuần hoàn

Cho hàm số y = f(x) với tập xác định D. Hàm số y = f(x) được gọi là tuần hoàn nếu tồn tại một số T khác 0 sao cho với mọi x ∈ D, ta có:

⦁ x + T ∈ D và x – T ∈ D;

⦁ f(x + T) = f(x).

Số T dương nhỏ nhất thỏa mãn các tính chất trên (nếu có) được gọi là chu kì của hàm số tuần hoàn đó.

Ví dụ 2. Cho hàm số f(x) = 4 và một số T dương.

Hàm số f(x) có phải là hàm số tuần hoàn không? Vì sao?

Hướng dẫn giải

Hàm số f(x) = 4, có:

⦁ Tập xác định là D = ℝ.

⦁ Nếu x ∈ ℝ thì x + T ∈ ℝ.

Tương tự, nếu x ∈ ℝ thì x – T ∈ ℝ.

⦁ Vì f(x) là hàm số hằng nên ∀x ∈ ℝ thì f(x) = 4.

Do đó f(x + T) = f(x) = 4.

Vậy hàm số f(x) = 4 là hàm số tuần hoàn với chu kì T, với T là một số dương bất kì.

Nhận xét: Cho hàm số tuần hoàn chu kì T. Từ đồ thị hàm số trên đoạn [a; a + T], ta dịch chuyển song song với trục hoành sang phải (hoặc sang trái) theo đoạn có độ dài T thì được đồ thị hàm số trên đoạn [a + T; a + 2T] (hoặc [a – T; a]).

2. Hàm số y = sinx

2.1. Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x với một số thực sinx được gọi là hàm số y = sinx.

Tập xác định của hàm số y = sinx là ℝ.

2.2. Đồ thị của hàm số y = sinx

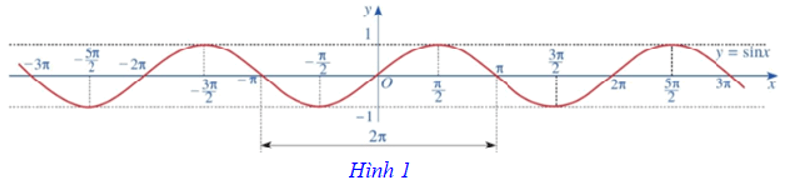
Ta có đồ thị của hàm số y = sinx trên ℝ được biểu diễn ở Hình 1:

2.3. Tính chất của hàm số y = sinx

Hàm số y = sinx có tập giá trị là [–1; 1] và có những tính chất sau:

⦁ Là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O;

⦁ Là hàm số tuần hoàn chu kì 2π;

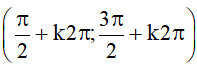
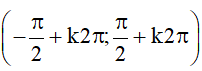
⦁ Là hàm số đồng biến trên mỗi khoảng , nghịch biến trên mỗi khoảng  với k ∈ ℤ.

Ví dụ 3.

+ Hàm số y = sinx đồng biến trên khoảng 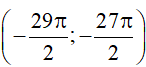 vì:

+ Hàm số y = sinx nghịch biến trên khoảng 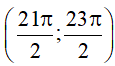 vì:

Nhận xét: Dựa vào đồ thị của hàm số y = sinx (Hình 1), ta thấy sinx = 0 tại những giá trị x = kπ (k ∈ ℤ). Vì vậy, tập hợp các số thực x sao cho sinx ≠ 0 là E = ℝ \ {kπ | k ∈ ℤ}.

3. Hàm số y = cosx

3.1. Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x với một số thực cosx được gọi là hàm số y = cosx.

Tập xác định của hàm số y = cosx là ℝ.

3.2. Đồ thị của hàm số y = cosx

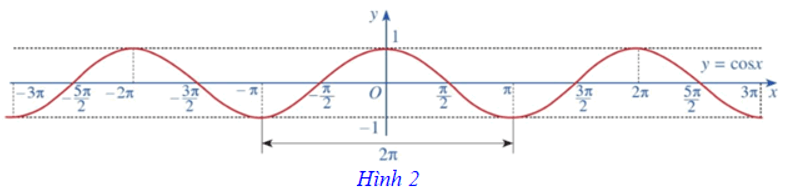
Ta có đồ thị của hàm số y = cosx trên ℝ được biểu diễn ở Hình 2.

3.3. Tính chất của hàm số y = cosx

Hàm số y = cosx có tập giá trị là [–1; 1] và có những tính chất sau:

⦁ Là hàm số chẵn, có đồ thị đối xứng qua trục tung;

⦁ Là hàm số tuần hoàn chu kì 2π;

⦁ Là hàm số đồng biến trên mỗi khoảng (–π + k2π; k2π), nghịch biến trên mỗi khoảng (k2π; π + k2π) với k ∈ ℤ.

Ví dụ 4.

+ Hàm số y = cosx đồng biến trên khoảng (5π; 6π) vì (5π; 6π) = (–π + 3.2π; 3.2π);

+ Hàm số y = cosx nghịch biến trên khoảng (–8π; –7π) vì (–8π; –7π) = (–4.2π; π + (–4).2π).

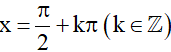
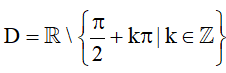
Nhận xét: Dựa vào đồ thị của hàm số y = cosx (Hình 2), ta thấy cosx = 0 tại những giá trị . Vì vậy, tập hợp các số thực x sao cho cosx ≠ 0 là .

4. Hàm số y = tanx

4.1. Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x ∈ D với một số thực tanx được gọi là hàm số y = tanx. Tập xác định của hàm số y = tanx là .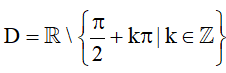

4.2. Đồ thị của hàm số y = tanx

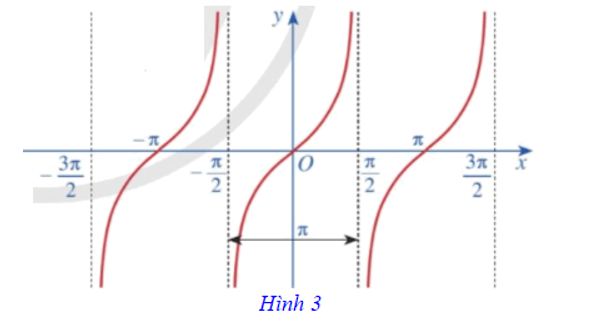
Ta có đồ thị hàm số y = tanx trên D được biểu diễn ở Hình 3.

4.3. Tính chất của hàm số y = tanx

Hàm số y = tanx có tập giá trị là ℝ và có những tính chất sau:

⦁ Là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O;

⦁ Là hàm số tuần hoàn chu kì π;

⦁ Là hàm số đồng biến trên mỗi khoảng 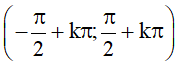 với k ∈ ℤ.

Ví dụ 5. Xét tính chẵn, lẻ của hàm số f(x) = sin2x.tanx.

Tập xác định của hàm số f(x) là .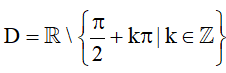

⦁ Với mọi x ∈ D, ta có –x ∈ D;

⦁ f(–x) = sin(–2x).tan(–x) = –sin2x.(–tanx) = sin2x.tanx = f(x).

Vậy hàm số f(x) = sin2x.tanx là hàm số chẵn.

5. Hàm số y = cotx

5.1. Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x ∈ E với một số thực cotx được gọi là hàm số y = cotx. Tập xác định của hàm số y = cotx là E = ℝ \ {kπ | k ∈ ℤ}.

5.2. Đồ thị của hàm số y = cotx

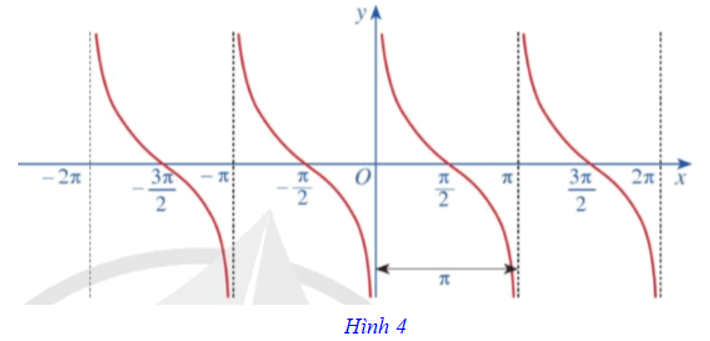
Ta có đồ thị hàm số y = cotx trên E được biểu diễn ở Hình 4.

5.3. Tính chất của hàm số y = cotx

Hàm số y = cotx có tập giá trị là ℝ và có những tính chất sau:

⦁ Là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O;

⦁ Là hàm số tuần hoàn chu kì π;

⦁ Là hàm số nghịch biến trên mỗi khoảng (kπ; π + kπ) với k ∈ ℤ.

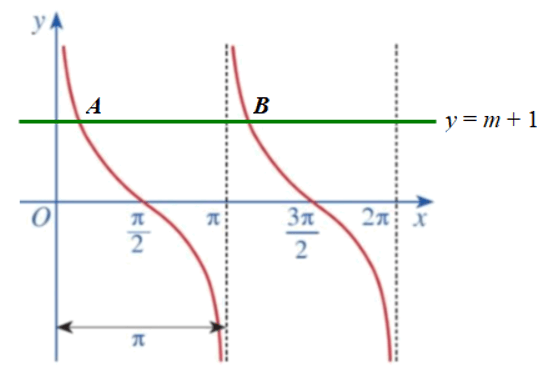
Ví dụ 6. Với mỗi số thực m, tìm số giao điểm của đường thẳng y = m + 1 và đồ thị hàm số y = cotx trên khoảng (0; 2π).

Hướng dẫn giải

Đồ thị hàm số y = cotx và đường thẳng y = m + 1 trên khoảng (0; 2π) được vẽ như sau:

Quan sát hình vẽ, ta thấy trên khoảng (0; 2π), đồ thị hàm số y = cotx (đường màu đỏ) cắt đường thẳng y = m + 1 (đường màu xanh lá) tại hai điểm A, B phân biệt.

Vậy số giao điểm của đường thẳng y = m + 1 và đồ thị hàm số y = cotx trên khoảng (0; 2π) là 2.

Bài tập Hàm số lượng giác và đồ thị

Bài 1. Xác định tham số m để:

a) Hàm số f(x) = 5m.sin4x + cos2x là hàm số chẵn.

b) Hàm số g(x) = (m – 1).tanx.cotx là hàm số lẻ.

Hướng dẫn giải

a) Hàm số f(x) có tập xác định là D = ℝ.

Ta có ∀x ∈ ℝ thì –x ∈ ℝ.

Để hàm số f(x) là hàm số chẵn thì f(–x) = f(x), ∀x ∈ ℝ.

⇔ 5m.sin(–4x) + cos(–2x) = 5m.sin4x + cos2x, ∀x ∈ ℝ.

⇔ –5m.sin4x + cos2x = 5m.sin4x + cos2x, ∀x ∈ ℝ.

⇔ 10m.sin4x = 0, ∀x ∈ ℝ.

⇔ m = 0.

Vậy m = 0 thỏa mãn yêu cầu bài toán.

b) Hàm số g(x) có tập xác định là .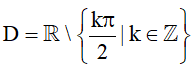

Ta có ∀x ∈ D thì –x ∈ D.

Để hàm số g(x) là hàm số lẻ thì f(–x) = –f(x), ∀x ∈ D.

⇔ (m – 1).tan(–x).cot(–x) = –(m – 1).tanx.cotx, ∀x ∈ D.

⇔ (m – 1).tanx.cotx = –(m – 1).tanx.cotx, ∀x ∈ D.

⇔ 2(m – 1).tanx.cotx = 0, ∀x ∈ D.

⇔ m – 1 = 0.

⇔ m = 1.

Vậy m = 1 thỏa mãn yêu cầu bài toán.

Bài 2. Chứng minh các hàm số sau là hàm số tuần hoàn:

a) f(x) = tan2x, với $T=\frac{3\pi }{2}$;

b) , với T = 3π.

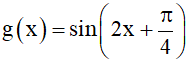
Hướng dẫn giải

a) Hàm số f(x) có tập xác định là .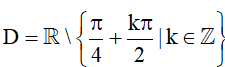

⦁ Ta có ∀x ∈ D thì $x+T=x+\frac{3\pi }{2}\in D$ và $x-T=x-\frac{3\pi }{2}\in D$.

⦁ Lại có 

Vậy hàm số f(x) = tan2x là hàm số tuần hoàn.

b) Hàm số g(x) có tập xác định là E = ℝ \ {kπ | k ∈ ℤ}.

⦁ Ta có ∀x ∈ E thì x + T = x + 3π ∈ E và x – T = x – 3π ∈ E.

Bài 3. Số giờ có ánh sáng mặt trời của một thành phố A trong ngày thứ t của năm 2017 (có 365 ngày) được cho bởi một hàm số 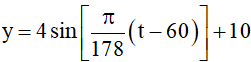, với t ∈ ℤ và 0 < t ≤ 365. Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?

Hướng dẫn giải

Ta có tập giá trị của hàm số y = sinx là [–1; 1].

Tức là, sinx ≤ 1.

⇔ y ≤ 14 (*)

Yêu cầu bài toán ⇔ Tìm t để y = 14, với 0 < t ≤ 365.

Ta có dấu “=” của (*) xảy ra khi và chỉ khi  (**)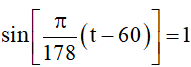

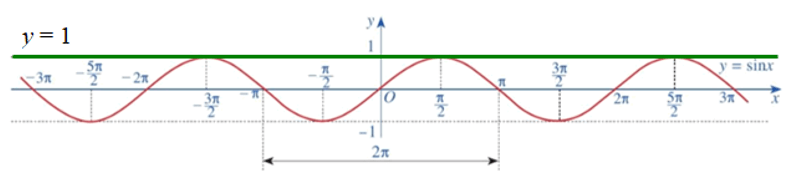
Quan sát hình vẽ, ta thấy đồ thị hàm số y = sinx cắt đường thẳng y = 1 tại $x=\frac{\pi }{2}+k2\pi$, với k ∈ ℤ.

Do đó (**) tương đương với: .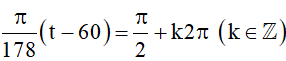

⇔ t – 60 = 89 + 356k (k ∈ ℤ).

⇔ t = 149 + 356k (k ∈ ℤ).

Vì 0 < t ≤ 365 nên 0 < 149 + 356k ≤ 365.

⇔ –149 < 356k ≤ 216.

$\iff -\frac{149}{356}<k\le \frac{54}{89}$.

Mà k ∈ ℤ nên k = 0.

Với k = 0, ta có: t = 149.

Vậy ngày 29 tháng 5 năm 2017 là ngày thành phố A có nhiều giờ có ánh sáng mặt trời nhất.

Xem thêm các bài tóm tắt lý thuyết Toán 11 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác

Lý thuyết Bài 2: Các phép biến đổi lượng giác

Lý thuyết Bài 4: Phương trình lượng giác cơ bản

Tổng hợp lý thuyết Toán 11 Chương 1

Lý thuyết Bài 1: Dãy số