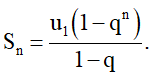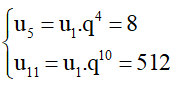Lý thuyết Toán 11 Bài 3: Cấp số nhân (Cánh diều)

Lý thuyết Toán 11 Bài 3: Cấp số nhân

1. Định nghĩa

Cấp số nhân là một dãy số, trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng tích của số hạng đứng ngay trước nó với một số không đổi q, tức là: u_n = u_{n – 1}.q với n ≥ 2.

Số q được gọi là công bội của cấp số nhân.

Chú ý:

– Khi q = 1 thì cấp số nhân là một dãy số không đổi.

– Nếu (u_n) là cấp số nhân với công bội q và u_n ≠ 0 với mọi n ≥ 1 thì với số tự nhiên n ≥ 2, ta có: $\frac{u_n}{u_{n-1}}=q$.

Ví dụ 1. Cho cấp số nhân (u_n) với u₁ = 2, công bội q = 3. Hãy viết ba số hạng đầu của cấp số nhân đó.

Hướng dẫn giải

Ba số hạng đầu của (u_n) là u₁ = 2; u₂ = u₁.3 = 2.3 = 6; u₃ = u₂.3 = 6.3 = 18.

Vậy u₁ = 2; u₂ = 6; u₃ = 18.

2. Số hạng tổng quát

Nếu cấp số nhân (u_n) có số hạng đầu là u₁ và công bội q thì số hạng tổng quát u_n được xác định bởi công thức:

u_n = u₁. q^{n – 1}  với n ≥ 2.

Ví dụ 2. Cho cấp số nhân (u_n)  với u₁ = –2, công bội q = –3. Hãy tính u₁₀.

Hướng dẫn giải

Theo công thức số hạng tổng quát của cấp số nhân, ta có:

u₁₀ = u₁. q^{10 – 1} = (–2).(–3)⁹ = 39366.

Vậy u₁₀ = 39366.

3. Tổng n số hạng đầu của một cấp số nhân

Cho cấp số nhân (u_n) có số hạng đầu u₁ và công bội q ≠ 1.

Đặt S_n = u₁ + u₂ + u₃ + … + u_n. Khi đó:

Chú ý: Nếu q = 1 thì S_n = nu₁.

Ví dụ 3. Hãy tính tổng S = 2 + 2² + 2³ + … + 2¹¹.

Hướng dẫn giải

S là tổng của 11 số hạng đầu của cấp số nhân có số hạng đầu u₁ = 2 và công bội q = 2.

Suy ra .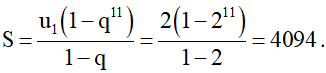

Vậy S = 4094.                                                                                     

Bài tập Cấp số nhân

Bài 1. Trong các dãy số sau, dãy số nào là cấp số nhân? Vì sao?

a) –2, 4, –8, 16, –32, 64, –128, 256.

b) 1, 4, 9, 16, 25, 36, 49, 64, 81, 100.

Hướng dẫn giải

a) Từ số hạng thứ hai của dãy số ta thấy số hạng sau gấp –2 lần số hạng trước của dãy.

Vì vậy dãy –2, 4, –8, 16, –32, 64, –128, 256 là cấp số nhân với số hạng đầu u₁ = –2 và công bội q = –2.

b) Ta có $\frac{4}{1}\ne \frac{9}{4}$ nên dãy 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 không phải là cấp số nhân.

Bài 2. Cho dãy số (u_n) có u_n = (–1)ⁿ⁺¹ . 3²ⁿ⁺¹. Chứng minh dãy (u_n) là một cấp số nhân. Chỉ rõ u₁ và công bội q.

Hướng dẫn giải

Ta xét tỉ số:

.

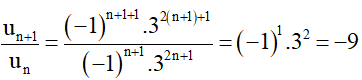
Suy ra dãy số (u_n) là một cấp số nhân có công bội q = –9 và u₁ = (–1)¹⁺¹ . 3^2.1+1 = 27.

Vậy u₁ = 27 và q = –9.

Bài 3. Cho cấp số nhân (u_n) có u₅ = 8 và u₁₁ = 512.

a) Tính số hạng đầu u₁ và công bội q của cấp số nhân (biết công bội q > 0).

b) Tính u₂₀ và S₂₀.

Hướng dẫn giải

a) Ta có 

Do q > 0 nên $\frac{u_{11}}{u_5}=\frac{u_1.q^{10}}{u_1.q^4}=q^6=64\Rightarrow q=2$ (do q > 0).

Thay q = 2 trở lại hệ ta được u₁ = $\frac{1}{2}$.

Vậy cấp số nhân đã cho có u₁ = $\frac{1}{2}$ và q = 2.

b) Ta có u₂₀ = u₁.q^{20 – 1} = u₁.q¹⁹ = $\frac{1}{2}{.2}^{19}=2^{18}=262144$.

.

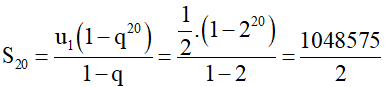
Vậy u₂₀ = 262144 và $S_{20}=\frac{1048575}{2}$.

Xem thêm các bài tóm tắt lý thuyết Toán 11 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 1: Dãy số

Lý thuyết Bài 2: Cấp số cộng

Tổng hợp lý thuyết Toán 11 Chương 2

Lý thuyết Bài 1: Giới hạn của dãy số

Lý thuyết Bài 2: Giới hạn của hàm số