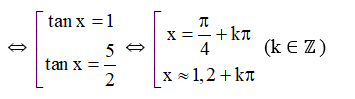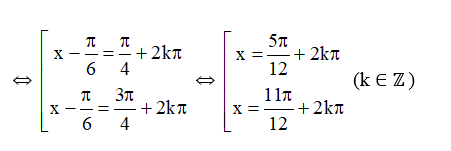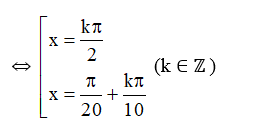Lý thuyết Toán 11 Bài 5: Phương trình lượng giác cơ bản (Chân trời sáng tạo)

Lý thuyết Toán 11 Bài 5: Phương trình lượng giác cơ bản

I. Lý thuyết

1. Phương trình tương đương

- Hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.

- Để chỉ sự tương đương của các phương trình, người ta dùng kí hiệu “⇔”.

Ví dụ: Hai phương trình x² – 9 = 0 và 3x² – 27 = 0 có cùng tập nghiệm {–3; 3} nên hai phương trình này tương đương.

2. Phương trình sin x = m

Xét phương trình sin x = m.

• Nếu |m| > 1 thì phương trình vô nghiệm.

• Nếu |m| ≤ 1 thì phương trình có nghiệm:

x = α + k2π, k ∈ ℤ

và x = π – α + k2π, k ∈ ℤ,

với α là góc thuộc [$\left[-\frac{\pi }{2};\frac{\pi }{2}\right]$] sao cho sin α = m.

Chú ý:

Một số trường hợp đặc biệt:

• sin x = 1 ⇔ $x=\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z};$              

• sin x = −1 ⇔ $x=-\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z};$

• sin x = 0 ⇔ x = $k\pi ,k\in \mathbb{Z}.$

Ta có:

• sin u = sin v ⇔ u = v + k2π, k ∈ ℤ hoặc u = π – v + k2π, k ∈ ℤ.

• sin x = sin a° ⇔ x = a° + k360°, k ∈ ℤ hoặc x = 180° − a° + k360°, k ∈ ℤ.

Ví dụ: $\sin x=\frac{\sqrt{3}}{2}\iff x=\frac{\pi }{3}+k2\pi$$x=\frac{2\pi }{3}+k2\pi \left(k\in \mathbb{Z}\right).$

3. Phương trình cos x = m

Xét phương trình cos x = m.

• Nếu |m| > 1 thì phương trình vô nghiệm.

• Nếu |m| ≤ 1 thì phương trình có nghiệm:

x = α + k2π, k ∈ ℤ

và x = – α + k2π, k ∈ ℤ,

với α là góc thuộc [0; π] sao cho cos α = m.

Chú ý:

Một số trường hợp đặc biệt:

• cos x = 1 ⇔ x = k2π, k ∈ ℤ;  

• cos x = −1 ⇔ x = π + k2π, k ∈ ℤ;

• cos x = 0 ⇔ $x=\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}.$

Ta có:

• cos u = cos v ⇔ u = v + k2π, k ∈ ℤ hoặc u = –v + k2π, k ∈ ℤ.

• cos x = cos a° ⇔ x = a° + k360°, k ∈ ℤ hoặc x = −a° + k360°, k ∈ ℤ.

Ví dụ: cos x = cos 15° ⇔ x = 15° + k360° hoặc x = −15° + k360°, k ∈ ℤ.

4. Phương trình tan x = m

Với mọi số thực m, phương trình tan x = m có nghiệm

x = α + kπ, k ∈ ℤ,

với α là góc thuộc $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ sao cho tan α = m.

Chú ý: tan x = tan a° ⇔ x = a° + k180°, k ∈ ℤ.

Ví dụ: tan x = 0 ⇔ x = kπ, k ∈ ℤ.

5. Phương trình cot x = m

Với mọi số thực m, phương trình cot x = m có nghiệm

x = α + kπ, k ∈ ℤ,

với α là góc thuộc (0; π) sao cho cot α = m.

Chú ý: cot x = cot a° ⇔ x = a° + k.180°, k ∈ ℤ.

Ví dụ: cot x = 1 ⇔ $x=\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}.$

6. Giải phương trình lượng giác bằng máy tính cầm tay

Ấn liên tiếp các phím SHIFT, sin/cos/tan và giá trị lượng giác của góc lượng giác bất kỳ để tìm ra góc lượng giác đó theo đơn vị radian hoặc theo đơn vị độ.

Chú ý: để giải phương trình cot x = m (m ≠ 0), ta giải phương trình $\tan x=\frac{1}{m}.$

II. Bài tập Phương trình lượng giác

Bài 1. Giải các phương trình lượng giác sau:

a) 2sin²x + 2sinx.cosx – 5cos²x = 0

b) $\sqrt{3}\sin x-\cos x=\sqrt{2}$

Hướng dẫn giải

a) $2si{n}^{2}x+2\sin x.\cos x-5co{s}^2\text{x}=0$

⇔ $2{\tan }^{2}x+3\tan x-5=0$

Vậy phương trình đã cho có nghiệm là $x=\frac{\pi }{4}+k\pi$ hoặc $x\approx 1,2+k\pi$ (k ∈ ℤ).

b) $\sqrt{3}\sin x-\cos x=\sqrt{2}$

⇔ $\frac{\sqrt{3}}{2}\sin x-\frac{1}{2}\cos x=\frac{\sqrt{2}}{2}$

⇔ $\sin x.\cos \frac{\pi }{6}-\cos x.\sin \frac{\pi }{6}=\frac{\sqrt{2}}{2}$

⇔ $\sin \left(x-\frac{\pi }{6}\right)=\sin \frac{\pi }{4}$

Vậy phương trình đã cho có nghiệm là $x=\frac{5\pi }{12}+2k\pi$ hoặc $x=\frac{11\pi }{12}+2k\pi$ (k ∈ ℤ).

Bài 2. Giải phương trình: cos3x.tan5x = sin7x.

Hướng dẫn giải

Điều kiện cos 5x ≠ 0

Khi đó phương trình đã cho trở thành

2sin5x.cos3x = 2sin7x.cos5x

⇔ sin8x = sin12x

• Với $x=\frac{k\pi }{2}$ thì ta có:

$\cos 5x=\cos \frac{5k\pi }{2}=\cos \left(\frac{k\pi }{2}+2k\pi \right)=\cos \left(\frac{k\pi }{2}\right)\ne 0$

⇔ k = 2m (m ∈ ℤ)

• Với $x=\frac{\pi }{20}+\frac{k\pi }{10}$ thì ta có:

$\cos 5x=\cos \left(\frac{\pi }{4}+\frac{k\pi }{2}\right)\ne 0$

 Vậy phương trình đã cho có nghiệm là $x=m\pi ;x=\frac{\pi }{20}+\frac{k\pi }{10}$ (m, k ∈ ℤ).

Bài 3. Tìm x ∈ [0; 14] sao cho: cos3x – 4cos2x + 3cos x – 4 = 0. (1)

Hướng dẫn giải

Ta có: cos3x = 4cos³x – 3cosx

(1) ⇔ cos3x + 3cos x – 4(1 + cos2x) = 0

⇔ 4cos³x – 8cos²x = 0

⇔ 4cos³x.(cos x – 2) = 0

⇔ cos x = 0

⇔ $x=\frac{\pi }{2}+k\pi$ (k ∈ ℤ)

Vì x ∈ [0; 14] ⇒ {$x\in \left\{\frac{\pi }{2};\frac{3\pi }{2};\frac{5\pi }{2};\frac{7\pi }{2}\right\}.$}

Vậy {$x\in \left\{\frac{\pi }{2};\frac{3\pi }{2};\frac{5\pi }{2};\frac{7\pi }{2}\right\}.$}

Xem thêm các bài tóm tắt lý thuyết Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 3: Các công thức lượng giác

Lý thuyết Bài 4: Hàm số lượng giác và đồ thị

Tổng hợp lý thuyết Toán 11 Chương 1

Lý thuyết Bài 1: Dãy số

Lý thuyết Bài 2: Cấp số cộng