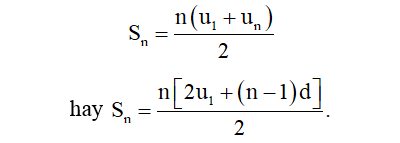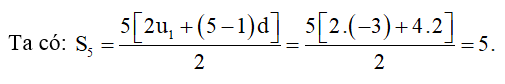Lý thuyết Toán 11 Bài 2: Cấp số cộng (Chân trời sáng tạo)

Lý thuyết Toán 11 Bài 2: Cấp số cộng

I. Lý thuyết

1. Cấp số cộng

- Cấp số cộng là một dãy số (vô hạn hoặc hữu hạn) mà trong đó, kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số hạng đứng ngay trước nó với một số d không đổi, nghĩa là:

u_{n + 1} = u_n + d với n ∈ ℕ*.

Số d được gọi là công sai của cấp số cộng.

Ví dụ: Cho cấp số cộng: $-\frac{1}{2};0;\frac{1}{2};\frac{3}{2};\mathrm{...}$ Tìm số hạng đầu, công sai và u₅.

Hướng dẫn giải

Cấp số cộng đã cho có số hạng đầu $u_1=-\frac{1}{2}$; công sai $d=\frac{1}{2}$.

Ta có $u_4=\frac{3}{2}$ nên $u_5=u_4+d=\frac{3}{2}+\frac{1}{2}=2.$

2. Số hạng tổng quát của cấp số cộng

Định lí 1: Nếu một cấp số cộng (u_n) có số hạng đầu u₁ và công sai d thì số hạng tổng quát u_n của nó được xác định bởi công thức:

u_n = u₁ + (n – 1)d, n ≥ 2.

Ví dụ: Cho một cấp số cộng có u₁ = −3; u₆ = 27.

Hướng dẫn giải

Ta có: u₆ = u₁ + (6 – 1)d = 27

⇔ −3 + 5d = 27 ⇔ 5d = 30 ⇔ d = 6.

3. Tổng của n số hạng đầu tiên của cấp số cộng

Định lí 2: Giả sử (u_n) là một cấp số cộng có công sai d. Đặt S_n = u₁ + u₂ + ... + u_n, khi đó

Ví dụ: Cho cấp số cộng (u_n) có u₁ = −3; d = 2.

Vậy tổng của 5 số hạng đầu tiên của dãy số (u_n) là 5.

II. Bài tập Cấp số cộng

Bài 1. Cho cấp số cộng (u_n) có u₁ = 321 và u_{n + 1} = u_n – 3, ∀n ∈ ℕ*. Số 99 là số hạng thứ bao nhiêu trong dãy số?

A. 72;

B. 73;

C. 74;

D. 75.

Hướng dẫn giải

Đáp án đúng là: D

Ta có: u_{n + 1} = u_n – 3 ⇒ u_{n + 1} − u_n = −3 ⇒ d = −3.

u_n = u₁ + (n – 1)d = 321 + (n – 1)(−3) = −3n + 324.

Ta có: u_n = 99 ⇒ −3n + 324 = 99

⇒ −3n = −225 ⇒ n = 75.

Vậy 99 là số hạng thứ 75 trong dãy số.

Bài 2. Cho cấp số cộng (u_n) có u₂ = 2017 và u₃ = 1945. Số hạng thứ 6 của cấp số cộng đã cho bằng bao nhiêu?

Hướng dẫn giải

Ta có u₃ – u₂ = 1945 – 2017 = –72 ⇒ d = −72.

⇒ u₁ = u₂ − d = 2017 + 72 = 2089.

u₆ = u₁ + 5d = 2089 + 5.(−72) = 1729.

Vậy số hạng thứ 6 của cấp số cộng đã cho là 1729.

Bài 3. Cho cấp số cộng (u_n) có $u_1=\frac{1}{3},u_8=26$ . Tìm d và xác định công thức số hạng tổng quát của cấp số cộng đã cho.

Hướng dẫn giải

Ta có <$u_8=u_1+7d \iff 26=\frac{1}{3}+7d$ 

$\iff 7d=\frac{77}{3}$$\iff d=\frac{11}{3}.$

Vậy công thức số hạng tổng quá

Xem thêm các bài tóm tắt lý thuyết Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Tổng hợp lý thuyết Toán 11 Chương 1

Lý thuyết Bài 1: Dãy số

Lý thuyết Bài 3: Cấp số nhân

Tổng hợp lý thuyết Toán 11 Chương 2

Lý thuyết Bài 1: Giới hạn của dãy số