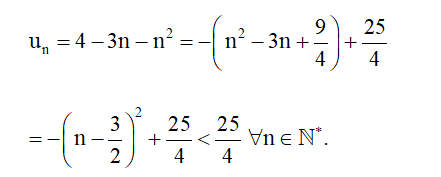Lý thuyết Toán 11 Bài 1: Dãy số (Chân trời sáng tạo)

Lý thuyết Toán 11 Bài 1: Dãy số

I. Lý thuyết

1. Dãy số là gì?

1.1. Dãy số vô hạn

- Hàm số u xác định trên tập các số nguyên dương ℕ* được gọi là một dãy số vô hạn (hay gọi tắt là dãy số), nghĩa là

$u:{\mathbb{N}}^{\ast }\to ℝ$

$n\mapsto u_n=u\left(n\right).$

- Ta có thể kí hiệu dãy số trên là (u_n), và (u_n) được viết dưới dạng khai triển là: u₁, u₂, u₃,...., u_n,....

- Số u₁ được gọi là số hạng đầu, u_n là số hạng thứ n và gọi là số hạng tổng quát của dãy số.

Chú ý:

• Số u₁ = u(1) được gọi là số hạng đầu, u_n = u(n) là số hạng thứ n hay số hạng tổng quát của dãy số.

• Nếu ∀n ∈ ℕ*, u_n = C thì (u_n) được gọi là dãy số không đổi.

Ví dụ:

+ Dãy số (u_n) bao gồm các số nguyên dương chia hết cho 3: 3; 6; 9; 12; ...

Ta có: dãy (u_n) có số hạng đầu u₁ = 3 và số hạng tổng quát u_n = 3n.

1.2. Dãy số hữu hạn

- Hàm số u xác định trên tập M = {1; 2; 3; ...; m} với ∀m ∈ ℕ* được gọi là một dãy số hữu hạn.

- Dãy số hữu hạn được khai triển dưới dạng u₁, u₂, u₃,...., u_m. Trong đó, u₁ được gọi là số hạng đầu, u_m được gọi là số hạng cuối.

Ví dụ:

+ Dãy số (u_n) bao gồm các số tự nhiên chẵn nhỏ hơn 10, sắp xếp theo thứ tự từ bé đến lớn.

Ta có: các số hạng của dãy số (u_n) là: 2; 4; 6; 8. Số hạng đầu của dãy số này là 2 và số hạng cuối của dãy số là 8.

2. Cách xác định dãy số

Một dãy số có thể được cho bằng các cách sau:

Cách 1: Liệt kê các số hạng (với các dãy số hữu hạn).

Cách 2: Cho công thức của số hạng tổng quát u_n.

Cách 3: Cho hệ thức truy hồi, nghĩa là:

• Cho số hạng thứ nhất u₁ (hoặc một vài số hạng đầu tiên).

• Cho một công thức tính un theo u_{n – 1} (hoặc theo vài số hạng đứng ngay trước nó).

Cách 4: Cho bằng cách mô tả.

Ví dụ:

+ Liệt kê các số hạng:

Cho dãy số (u_n) gồm tất cả các số lẻ lớn hơn 12: 13; 15; 17; ...

+ Công thức của số hạng tổng quát:

Cho công thức của số hạng tổng quát: u_n = 3n – 1.

+ Hệ thức truy hồi:

Cho dãy số (u_n) xác định bằng hệ thức truy hỏi: u₁ = 2, u_n = 5u_{n – 1} + 1 với n ≥ 2.

+ Phương pháp mô tả:

Cho dãy số (u_n) gồm tất cả các số nguyên tố theo thứ tự giảm dần.

3. Dãy số tăng, dãy số giảm

- Dãy số (u_n) là dãy số tăng nếu u_{n + 1} > u_n với mọi n ∈ ℕ*.

- Dãy số (u_n) là dãy số giảm nếu u_{n + 1} < u_n với mọi n ∈ ℕ*.

Ví dụ: Cho dãy số (u_n) với u_n = −5n + 3.

Ta có: u_{n + 1} – u_n = −5(n + 1) + 3 – (−5n + 3)

= −5n − 5 + 3 + 5n − 15 = −17 < 0 (tức là u_{n + 1} < u_n, ∀n ∈ ℕ*).

Vậy (u_n) là dãy số giảm.

4. Dãy số bị chặn

- Dãy số (u_n) được gọi là dãy số bị chặn trên nếu tồn tại một số M sao cho

u_n ≤ M, ∀n ∈ ℕ*.

- Dãy số (u_n) được gọi là dãy số bị chặn dưới nếu tồn tại một số M sao cho

u_n ≥ M, ∀n ∈ ℕ*.

- Dãy số (u_n) được gọi là dãy số bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, nghĩa là tồn tại các số m và M sao cho

M ≤ u_n ≤ M, ∀n ∈ ℕ*.

Ví dụ: Cho dãy số (u_n) với u_n = n – 2.

Dãy số (u_n) bị chặn dưới, vì u_n = n – 2 > −2, ∀n ∈ ℕ*.

II. Bài tập Dãy số

Bài 1. Cho dãy số (u_n) được xác định bởi $u_n=\frac{n+1}{2^n}$ với n ∈ ℕ*.

a) Liệt kê 3 số hạng đầu của dãy số (u_n).

b) Xét tính tăng, giảm của dãy số (u_n).

Hướng dẫn giải

a) Ta có: $u_1=\frac{1+1}{2^1}=1,u_2=\frac{2+1}{2^2}=\frac{3}{4},u_3=\frac{3+1}{2^3}=\frac{1}{2}.$

b) Ta có: $u_{n+1}-u_n=\frac{\left(n+1\right)+1}{2^{n+1}}-\frac{n+1}{2^n}$

$=\frac{n+2}{{2.2}^n}-\frac{n+1}{2^n}=\frac{n+2-2n-2}{{2.2}^n}=\frac{-n}{2^{n+1}}<0$

⇔ u_{n + 1} < u_n.

Vậy (u_n) là dãy số giảm.

Bài 2. Xét tính bị chặn của dãy số sau: u_n = 4 – 3n – n².

Hướng dẫn giải

Ta có: u_{n + 1} – u_n = 4 – 3(n + 1) – (n + 1)² – (4 – 3n – n²)

= 4 – 3n – 3 – n² – 2n – 1 – 4 + 3n + n²

= − 2n − 4

⇔ u_{n + 1} < u_n.

⇒ (u_n) là dãy số giảm, tức là n càng tăng thì u_n càng giảm ⇒ (u_n) không bị chặn dưới.

Vậy (u_n) là dãy số bị chặn trên.

Bài 3. Cho dãy số (u_n) bởi hệ thức truy hồi: $u_1=\frac{1}{2},u_{n+1}=2u_n.$ Tìm ra công thức số hạng tổng quát của dãy số này.

Hướng dẫn giải

Ta có: $u_1=\frac{1}{2}=2^{-1};u_2=1=2^0;u_3=2=2^1;u_4=4=2^2.$

Ta nhận thấy u₁ = 2^{1 – 2}; u₂ = 2^{2 – 2}; u₃ = 2^{3 – 2}; u₄ = 2^{4 – 2}.

Vậy công thức số hạng tổng quát của dãy số (u_n) là u_n = 2^{n – 2}.

Bài 4. Cho dãy số (u_n), biết $u_n=\frac{n+1}{2n+1}.$ Số $\frac{8}{15}$ là số hạng thứ mấy của dãy số?

A. 8;                               

B. 6;                                

C. 5;                                

D. 7.

Hướng dẫn giải

Đáp án đúng là: D

Ta cần tìm n sao cho $u_n=\frac{n+1}{2n+1}=\frac{8}{15}\iff 15n+15=16n+8\iff n=7.$

Xem thêm các bài tóm tắt lý thuyết Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 5: Phương trình lượng giác cơ bản

Tổng hợp lý thuyết Toán 11 Chương 1

Lý thuyết Bài 2: Cấp số cộng

Lý thuyết Bài 3: Cấp số nhân

Tổng hợp lý thuyết Toán 11 Chương 2