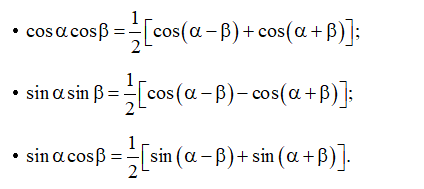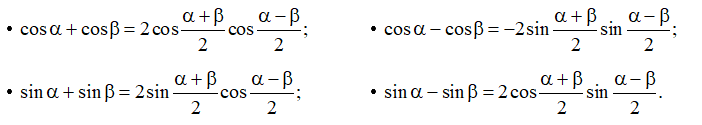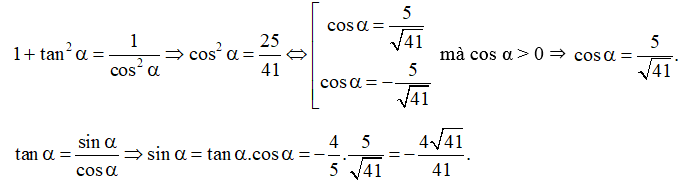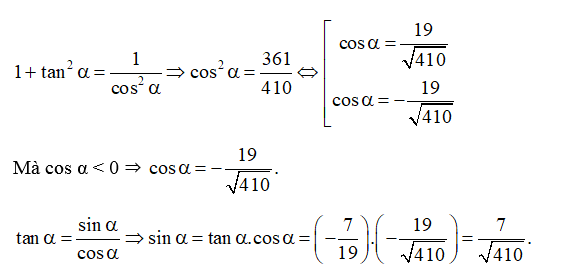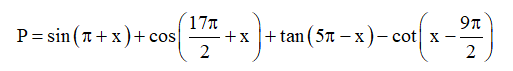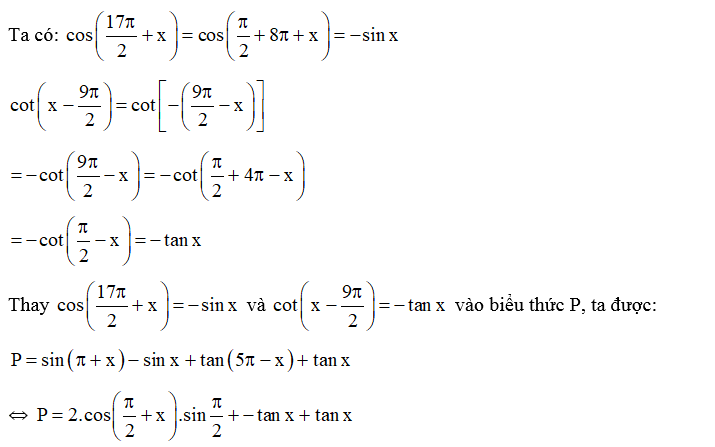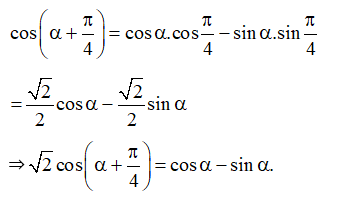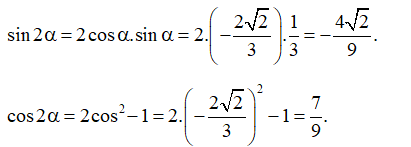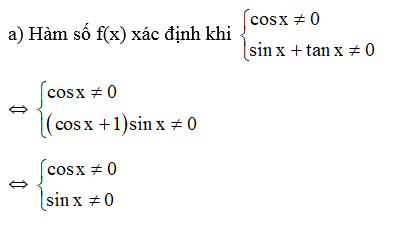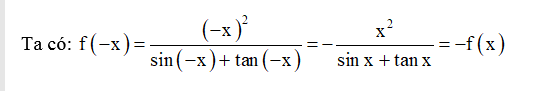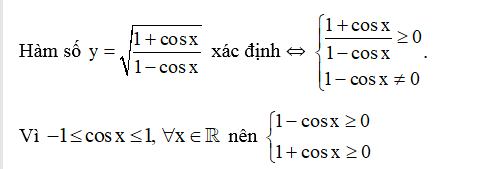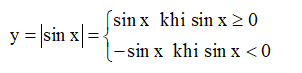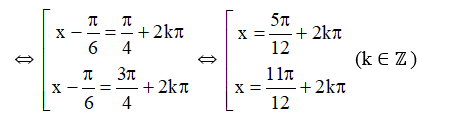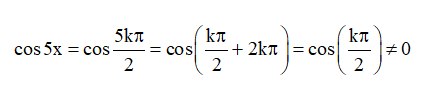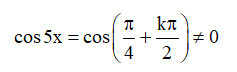Lý thuyết Toán 11 Chương 1: Hàm số lượng giác và phương trình lượng giác (Chân trời sáng tạo)

Lý thuyết Toán 11 Chương 1: Hàm số lượng giác và phương trình lượng giác

I. Lý thuyết

1. Góc lượng giác

1.1. Khái niệm

Cho hai tia Oa, Ob:

- Nếu một tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob, kí hiệu (Oa, Ob) = α.

- Khi tia Om quay một góc α, ta nói số đo của góc lượng giác (Oa, Ob) bằng α, kí hiệu sđ(Oa, Ob) = α.

- Số đo của các góc lượng giác có cùng tia đầu Oa và tia cuối Ob khác nhau một bội nguyên của 360° nên có công thức tổng quát là:

sđ(Oa, Ob) = α° + k . 360° (k ∈ ℤ), thường viết là (Oa, Ob) = α° + k . 360°

với α° là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.

Chú ý:

• Với hai tia Oa và Ob cho trước, có vô số góc lượng giác tia đầu Oa và tia cuối Ob. Ta dùng chung kí hiệu (Oa, Ob) cho tất cả các góc lượng giác này.

1.2. Hệ thức Chasles (Sa – lơ)

Với ba tia Oa, Ob và Oc bất kì, ta có:

(Oa, Ob) + (Ob, Oc) = (Oa, Oc) + k . 360° (k ∈ ℤ).

2. Đơn vị radian

- Trên đường tròn bán kính R tùy ý, góc ở tâm chắn một cung có độ dài đúng bằng R được gọi là một góc có số đo 1 radian (đọc là 1 ra – đi – an, viết tắt là 1 rad).

- Công thức chuyển đổi số đo góc từ đơn vị radian sang độ và ngược lại như sau:

$\alpha °=\frac{\pi \alpha }{180}rad$

hoặc $\alpha rad={\left(\frac{180\alpha }{\pi }\right)}^o.$

Chú ý:

• Khi ghi số đo của một góc theo đơn vị radian, người ta thường bỏ đi chữ rad sau số đo. Ví dụ, $\frac{\pi }{2}rad$ được viết là $\frac{\pi }{2}$, 2 rad được viết là 2.

• Với đơn vị radian, công thức số đo tổng quát của một góc lượng giác (Oa, Ob) là

(Oa, Ob) = α + k2p (k ∈ ℤ),

trong đó α là số đo theo radian của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob. Lưu ý không được viết α + k.360° hay α° + k2$\pi$ (vì không cùng đơn vị đo).

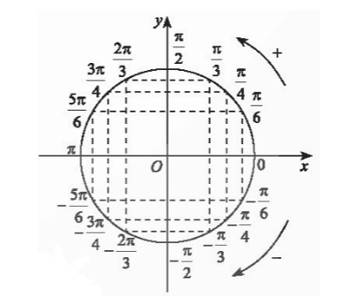
3. Đường tròn lượng giác

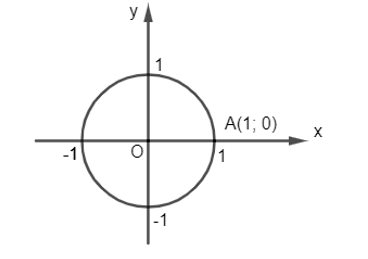
- Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm O bán kính bằng 1. Trên đường tròn này, chọn điểm A(1; 0) làm gốc, chiều dương là chiều ngược chiều kim đồng hồ và chiều âm là chiều cùng chiều kim đồng hồ. Đường tròn cùng với gốc và chiều như trên được gọi là đường tròn lượng giác.

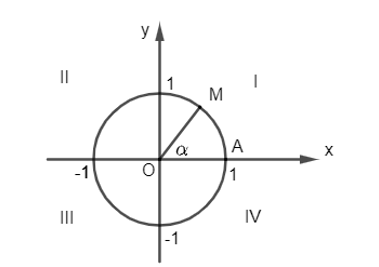
- Cho số đo góc α bất kì. Trên đường tròn lượng giác, ta xác định được duy nhất một điểm M sao cho số đo góc lượng giác (OA, OM) bằng α. Khi đó M được gọi là điểm biểu diễn của góc có số đo α trên đường tròn lượng giác.

Chú ý:

• Hệ trục tọa độ Oxy chia mặt phẳng tọa độ thành bốn “góc phần tư” kí hiệu lần lượt là I, II, III và IV.

4. Giá trị lượng giác của góc lượng giác

- Trên đường tròn lượng giác, gọi M là điểm biểu diễn góc lượng giác có số đo α. Khi đó:

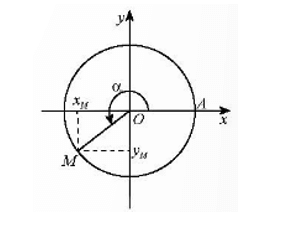
• Tung độ y_M của M gọi là sin của α, kí hiệu sin α.

• Hoành độ x_M của M gọi là côsin của α, kí hiệu cos α.

• Nếu x_M ≠ 0 thì tỉ số $\frac{y_M}{x_M}=\frac{\sin \alpha }{\cos \alpha }$ gọi là tang của α, kí hiệu tan α.

• Nếu y_M ≠ 0 thì tỉ số $\frac{x_M}{y_M}=\frac{\cos \alpha }{\sin \alpha }$ gọi là côtang của α, kí hiệu cot α.

Các giá trị sin α, cos α, tan α và cot α được gọi là các giá trị lượng giác của góc lượng giác α.

Chú ý:

• Ta gọi trục hoành là trục côsin, còn trục tung là trục sin.

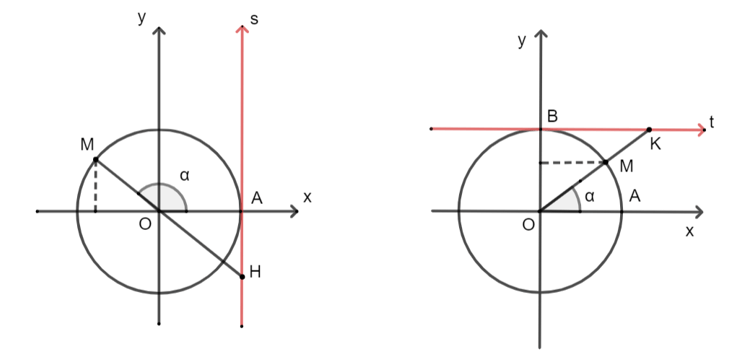
• Trục As có gốc ở điểm A(1; 0) và song song với trục sin gọi là trục tang. Nếu đường thẳng OM cắt trục tang thì tung độ của giao điểm đó chính là tan α.

• Trục Bt có gốc ở điểm B(0; 1) và song song với trục côsin gọi là trục côtang. Nếu đường thẳng OM cắt trục côtang thì hoành độ của giao điểm đó chính là cot α.

• sin α và cos α xác định với mọi α ∈ ℝ;

tan α chỉ xác định với các góc $\alpha \ne \frac{\pi }{2}+k\pi \text{\hspace{0.17em}\hspace{0.17em}(}\left(k\in \mathbb{Z}\right);$)

cot α chỉ xác định với các góc α ≠ kπ (k ∈ ℤ).

• Với mọi góc lượng giác α và số nguyên k, ta có:

sin(α + k2π) = sin α;                            tan(α + kπ) = tan α;

cos(α + k2π) = cos α;                           cot(α + kπ) = cot α.

• Ta có thể sử dụng đường tròn lượng giác để xác định giá trị lượng giác của góc α.

5. Tính giá trị lượng giác của một góc bằng máy tính cầm tay

Giá trị lượng giác của một góc bất kỳ có thể tính bằng máy tính cầm tay.

Chú ý:

• Trước khi tính, cần chọn đơn vị đo góc bằng cách:

+ Ấn các phím SHIFT, MENU và 2 để màn hình hiện lên bảng lựa chọn đơn vị đo góc bao gồm: Degree, Radian và Gradian.

+ Tiếp tục ấn phím 1 để chọn đơn vị độ (Degree) hoặc phím 2 để chọn đơn vị radian (Radian).

+ Cuối cùng ấn phím MENU và 1 để vào chế độ tính toán.

6. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác

Ta có những hệ thức sau liên hệ giữa các giá trị lượng giác của cùng một góc lượng giác α:

• sin²α + cos²α = 1                                        

• tan α . cot α = 1 với $\alpha \ne k\frac{\pi }{2},$ k ∈ ℤ

• $1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha }$ với $\alpha \ne \frac{\pi }{2}+k\pi ,$ k ∈ ℤ 

• $1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }$ với α ≠ kπ, k ∈ ℤ

7. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt

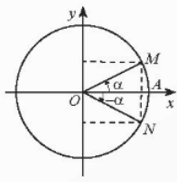
7.1. Hai góc đối nhau: 𝛂 và –𝛂

Các điểm biểu diễn của hai góc α và –α đối xứng qua trục Ox nên ta có: • sin(–α) = −sin α; • cos(–α) = cos α; • tan(–α) = −tan α; • cot(–α) = −cot α.

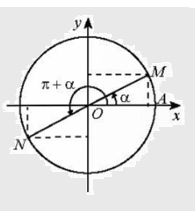
7.2. Hai góc hơn kém nhau 𝛑: 𝛂 và 𝛂 + 𝛑

Các điểm biểu diễn của hai góc α và α + π đối xứng nhau qua gốc tọa độ O nên ta có: • sin(α + π) = −sin α; • cos(α + π) = −cos α; • tan(α + π) = tan α; • cot(α + π) = cot α.

 

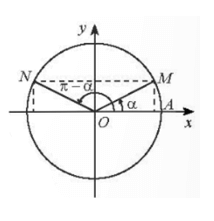
7.3. Hai góc bù nhau: 𝛂 và 𝛑 – 𝛂

Các điểm biểu diễn của hai góc α và π – α đối xứng nhau qua trục Oy nên ta có: • sin(π – α) = sin α; • cos(π – α) = −cos α; • tan(π – α) = −tan α; • cot(π – α) = −cot α.

 

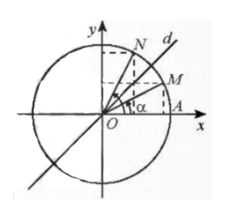
7.4. Hai góc phụ nhau: 𝛂 và $\frac{\pi }{2}-\alpha$

Các điểm biểu diễn của hai góc α và $\frac{\pi }{2}-\alpha$ đối xứng nhau qua đường phân giác d của góc xOy nên ta có: • $\mathrm{sin(}\left(\frac{\pi }{2}-\alpha \right))=\cos \alpha ;$              • $\mathrm{tan(}\left(\frac{\pi }{2}-\alpha \right))=\cot \alpha ;$ • $\mathrm{cos(}\left(\frac{\pi }{2}-\alpha \right))=\sin \alpha ;$             • $\mathrm{cot(}\left(\frac{\pi }{2}-\alpha \right))=\tan \alpha .$

8. Công thức cộng

• cos(α + β) = cosα.cosβ – sinα.sinβ;            

• cos(α – β) = cosα.cosβ + sinα.sinβ;

• sin(α + β) = sinα.cosβ + cosα.sinβ;             

• sin(α – β) = sinα.cosβ − cosα.sinβ;

• $\tan \left(\alpha +\beta \right)=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta };$                        

• $\tan \left(\alpha -\beta \right)=\frac{\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }.$

9. Công thức góc nhân đôi

- Công thức góc nhân đôi là công thức tính các giá trị lượng giác của góc 2α qua các giá trị lượng giác của góc α.

- Công thức góc nhân đôi bao gồm những công thức sau:

• cos2α = cos²α – sin²α = 2cos²α – 1 = 1 – 2sin²α;

• sin2α = 2sinα . cosα;

• $\tan 2\alpha =\frac{2\tan \alpha }{1-{\tan }^2\alpha }.$

10. Công thức biến đổi tích thành tổng

11. Công thức biến đổi tổng thành tích

12. Hàm số lượng giác

- Hàm số sin là quy tắc đặt tương ứng mỗi số thực x với số thực sin x, kí hiệu y = sin x.

- Hàm số côsin là quy tắc đặt tương ứng mỗi số thực x với số thực cos x, kí hiệu          y = cos x.

- Hàm số tang là hàm số được xác định bởi công thức

$y=\frac{\sin x}{\cos x}$ với $x\ne \frac{\pi }{2}+k\pi$ (k ∈ ℤ), kí hiệu y = tan x.

- Hàm số côtang là hàm số được xác định bởi công thức

$y=\frac{\cos x}{\sin x}$ với x ≠ kπ (k ∈ ℤ), kí hiệu y = cot x.

Chú ý:

• Tập xác định của hàm số y = sin x và y = cos x là ℝ.

• Tập xác định của hàm số y = tan x là D = ℝ \ {$\frac{\pi }{2}$+ kπ| k ∈ ℤ}.

• Tập xác định của hàm số y = cot x là D = ℝ \ { kπ| k ∈ ℤ}.

13. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

13.1. Hàm số chẵn, hàm số lẻ

- Hàm số y = f(x) với tập xác định D được gọi là hàm số chẵn nếu với mọi x ∈ D ta có    – x ∈ D và f(−x) = f(x).

- Hàm số y = f(x) với tập xác định D được gọi là hàm số lẻ nếu với mọi x ∈ D ta có              – x ∈ D và f(−x) = −f(x).

Chú ý:

• Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.

• Đồ thị của hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

13.2. Hàm số tuần hoàn

- Hàm số y = f(x) với tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại một số T khác 0 sao cho với mọi x ∈ D ta có x ± T ∈ D và f(x + T) = f(x).

- Số T dương nhỏ nhất thỏa mãn các điều kiện trên (nếu có) được gọi là chu kì của hàm số tuần hoàn y = f(x).

Chú ý:

• Đồ thị của hàm số tuần hoàn chu kì T được lặp lại trên từng đoạn giá trị của x có độ dài T.

• Các hàm số y = sin x và y = cos x là các hàm số tuần hoàn với chu kì 2π.

• Các hàm số y = tan x và y = cot x là các hàm số tuần hoàn với chu kì π.

14. Đồ thị của các hàm số lượng giác

14.1. Hàm số y = sin x

Hàm số y = sin x có tập xác định là ℝ, tập giá trị là [−1; 1] và có các tính chất sau:

- Hàm số tuần hoàn với chu kì 2π.

- Hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O.

- Hàm số đồng biến trên các khoảng ($\left(-\frac{\pi }{2}+2k\pi ;\frac{\pi }{2}+2k\pi \right)\text{\hspace{0.17em})(}\left(k\in \mathbb{Z}\right)$) và nghịch biến trên các khoảng ($\left(\frac{\pi }{2}+2k\pi ;\frac{3\pi }{2}+2k\pi \right)\text{\hspace{0.17em}\hspace{0.17em})(}\left(k\in \mathbb{Z}\right).$)

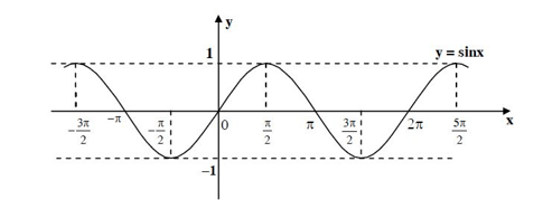
Đồ thị của hàm số y = sin x trên ℝ như sau:

Chú ý:

• Vì y = sin x là hàm số lẻ nên để vẽ đồ thị của nó trên đoạn [−π; π], ta có thể vẽ trên đoạn [0; π], sau đó lấy đối xứng qua gốc tọa độ.

14.2. Hàm số y = cos x

Hàm số y = cos x có tập xác định là ℝ, tập giá trị là [−1; 1] và có các tính chất sau:

- Hàm số tuần hoàn với chu kì 2π.

- Hàm số chẵn, có đồ thị đối xứng qua trục Oy.

- Hàm số đồng biến trên các khoảng ($\left(-\pi +2k\pi ;2k\pi \right)\text{\hspace{0.17em}\hspace{0.17em})(}\left(k\in \mathbb{Z}\right)$) và nghịch biến trên các khoảng ($\left(2k\pi ;\pi +2k\pi \right)\text{\hspace{0.17em}\hspace{0.17em})(}\left(k\in \mathbb{Z}\right).$)

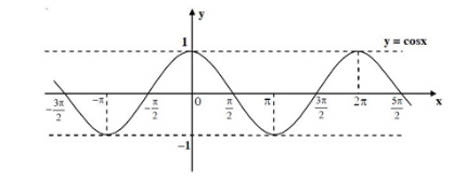
Đồ thị của hàm số y = cos x trên ℝ như sau:

Chú ý:

• Vì y = cos x là hàm số chẵn nên để vẽ đồ thị của nó trên đoạn [−π; π], ta có thể vẽ trên đoạn [0; π], sau đó lấy đối xứng qua trục tung.

14.3. Hàm số y = tan x

Hàm số y = tan x có tập xác định là ℝ \ {$\frac{\pi }{2}$+ kπ| k ∈ ℤ}, tập giá trị là $\mathrm{ℝ}$ và có các tính chất sau:

- Hàm số tuần hoàn với chu kì π.

- Hàm số lẻn, có đồ thị đối xứng qua gốc tọa độ O.

- Hàm số đồng biến trên các khoảng ($\left(-\frac{\pi }{2}+k\pi ;\frac{\pi }{2}+k\pi \right)\text{\hspace{0.17em}\hspace{0.17em})(}\left(k\in \mathbb{Z}\right).$)

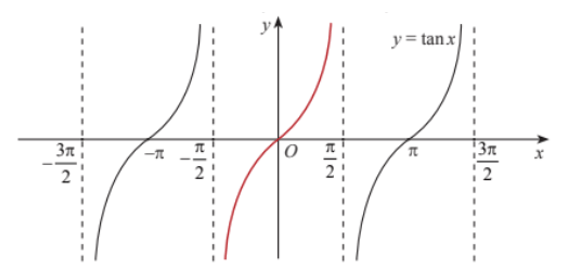
Đồ thị của hàm số y = tan x trên ℝ \ {$\frac{\pi }{2}$+ kπ| k ∈ ℤ} như sau:

Chú ý:

• Vì y = tan x là hàm số lẻ nên để vẽ đồ thị của nó trên khoảng ($\left(-\frac{\pi }{2};\frac{\pi }{2}\right),$) ta có thể vẽ trên nửa khoảng [$\left[0;\frac{\pi }{2}\right),$) sau đó lấy đối xứng qua gốc tọa độ.

14.4. Hàm số y = cot x

Hàm số y = cot x có tập xác định là ℝ \ {kπ| k ∈ ℤ} tập giá trị là $\mathrm{ℝ}$ và có các tính chất sau:

- Hàm số tuần hoàn với chu kì π.

- Hàm số lẻn, có đồ thị đối xứng qua gốc tọa độ O.

- Hàm số nghịch biến trên các khoảng ($\left(k\pi ;\pi +k\pi \right)\text{\hspace{0.17em}\hspace{0.17em})(}\left(k\in \mathbb{Z}\right)).$

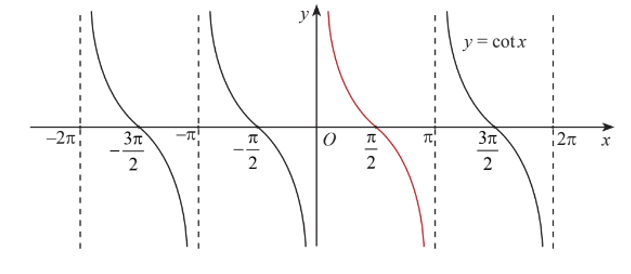
Đồ thị của hàm số y = cot x trên ℝ \ {kπ| k ∈ ℤ}. như sau:

15. Phương trình tương đương

- Hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.

- Để chỉ sự tương đương của các phương trình, người ta dùng kí hiệu “⇔”.

Ví dụ: Hai phương trình x² – 9 = 0 và 3x² – 27 = 0 có cùng tập nghiệm {–3; 3} nên hai phương trình này tương đương.

16. Phương trình sin x = m

Xét phương trình sin x = m.

• Nếu |m| > 1 thì phương trình vô nghiệm.

• Nếu |m| ≤ 1 thì phương trình có nghiệm:

x = α + k2π, k ∈ ℤ

và x = π – α + k2π, k ∈ ℤ,

với α là góc thuộc [$\left[-\frac{\pi }{2};\frac{\pi }{2}\right]$] sao cho sin α = m.

Chú ý:

Một số trường hợp đặc biệt:

• sin x = 1 ⇔ $x=\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z};$                

• sin x = −1 ⇔ $x=-\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z};$

• sin x = 0 ⇔ x = $k\pi ,k\in \mathbb{Z}.$

Ta có:

• sin u = sin v ⇔ u = v + k2π, k ∈ ℤ hoặc u = π – v + k2π, k ∈ ℤ.

• sin x = sin a° ⇔ x = a° + k360°, k ∈ ℤ hoặc x = 180° − a° + k360°, k ∈ ℤ.

17. Phương trình cos x = m

Xét phương trình cos x = m.

• Nếu |m| > 1 thì phương trình vô nghiệm.

• Nếu |m| ≤ 1 thì phương trình có nghiệm:

x = α + k2π, k ∈ ℤ

và x = – α + k2π, k ∈ ℤ,

với α là góc thuộc [0; π] sao cho cos α = m.

Chú ý:

Một số trường hợp đặc biệt:

• cos x = 1 ⇔ x = k2π, k ∈ ℤ;  

• cos x = −1 ⇔ x = π + k2π, k ∈ ℤ;

• cos x = 0 ⇔ $x=\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}.$

Ta có:

• cos u = cos v ⇔ u = v + k2π, k ∈ ℤ hoặc u = –v + k2π, k ∈ ℤ.

• cos x = cos a° ⇔ x = a° + k360°, k ∈ ℤ hoặc x = −a° + k360°, k ∈ ℤ.

18. Phương trình tan x = m

Với mọi số thực m, phương trình tan x = m có nghiệm

x = α + kπ, k ∈ ℤ,

với α là góc thuộc ($\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$) sao cho tan α = m.

Chú ý: tan x = tan a° ⇔ x = a° + k180°, k ∈ ℤ.

Ví dụ: tan x = 0 ⇔ x = kπ, k ∈ ℤ.

19. Phương trình cot x = m

Với mọi số thực m, phương trình cot x = m có nghiệm

x = α + kπ, k ∈ ℤ,

với α là góc thuộc (0; π) sao cho cot α = m.

Chú ý: cot x = cot a° ⇔ x = a° + k.180°, k ∈ ℤ.

20. Giải phương trình lượng giác bằng máy tính cầm tay

Ấn liên tiếp các phím SHIFT, sin/cos/tan và giá trị lượng giác của góc lượng giác bất kỳ để tìm ra góc lượng giác đó theo đơn vị radian hoặc theo đơn vị độ.

Chú ý: để giải phương trình cot x = m (m ≠ 0), ta giải phương trình $\tan x=\frac{1}{m}.$

II. Bài tập tổng hợp Toán 11 Chương 1

Bài 1. Đổi số đo của các góc sau đây sang radian:

a) −125°;

b) 42°;

Hướng dẫn giải

a) Ta có: $-125°=\frac{\pi .(-125)}{180}rad=-\frac{25\pi }{36}rad.$

b) Ta có: $42°=\frac{42\pi }{180}rad=\frac{7\pi }{30}rad.$

Bài 2. Đổi số đo của các góc sau đây sang độ:

a) $\frac{3\pi }{7};$

b) $\frac{2\pi }{9};$

Hướng dẫn giải

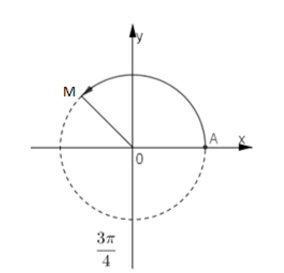
Bài 3. Biểu diễn trên đường tròn lượng giác góc lượng giác có số đo 135°:

Hướng dẫn giải

Ta có: $135°=45°+\frac{1}{4}.360°.$

Vậy điểm biểu diễn góc lượng giác có số đo 135° là điểm M nằm trên phần đường tròn lượng giác thuộc góc phần tư thứ II sao cho $\widehat{AOM}=135°.$

Bài 4. Tính các giá trị lượng giác của góc α biết:

a) $\tan \alpha =-\frac{4}{5}$biết $\frac{3\pi }{2}<\alpha <2\pi .$

b) $\cot \alpha =-\frac{19}{7}$ biết $\frac{\pi }{2}<\alpha <\pi .$

Hướng dẫn giải

a) Do $\frac{3\pi }{2}<\alpha <2\pi$ nên sin α < 0, cos α > 0, cot α < 0.

Ta có: $\cot \alpha =\frac{1}{\tan \alpha }\Rightarrow \cot \alpha =-\frac{5}{4}.$

b) Do $\frac{\pi }{2}<\alpha <\pi$ nên sin α > 0, cos α < 0, tan α < 0.

Ta có: $\tan \alpha =\frac{1}{\cot \alpha }\Rightarrow \tan \alpha =-\frac{7}{19}.$

Bài 5. Rút gọn các biểu thức sau:

a) A = (1 – sin²α).cot²α + 1 – cot²α;

b) $B=\frac{2{\cos }^2\alpha -1}{\sin \alpha +\cos \alpha }$.

Hướng dẫn giải

a) A = (1 – sin²α).cot²α + 1 – cot²α

⇔ A = cot²α – sin²α.cot²α + 1 – cot²α

⇔ $A=1-{\sin }^2\alpha .\frac{{\cos }^2\alpha }{{\sin }^2\alpha }={\sin }^2\alpha .$

b) $B=\frac{2{\cos }^2\alpha -1}{\sin \alpha +\cos \alpha }$

⇔ $B=\frac{{\cos }^2\alpha -{\sin }^2\alpha }{\sin \alpha +\cos \alpha }$

⇔ B = cos α – sin α.

Bài 6. Cho $\tan \alpha =\frac{3}{5}.$ Tính: $A=\frac{\sin \alpha \cos \alpha }{{\sin }^2\alpha -{\cos }^2\alpha }.$

Hướng dẫn giải

Chia cả tử và mẫu của biểu thức A cho cos²α ta được:

$A=\frac{\sin \alpha \cos \alpha }{{\sin }^2\alpha -{\cos }^2\alpha }=\frac{\tan \alpha }{{\tan }^2\alpha -1}=-\frac{15}{16}.$

Bài 1. Rút gọn biểu thức sau:

Hướng dẫn giải

⇔ P = −2sin x

Vậy P = −2sin x.

Bài 7. Chứng minh rằng: $\cos \alpha -\sin \alpha =\sqrt{2}\mathrm{cos(}\left(\alpha +\frac{\pi }{4}\right)).$

Hướng dẫn giải

Ta có:

Bài 8. Cho $\sin \alpha =\frac{1}{3}$ và $\frac{\pi }{2}<\alpha <\pi .$ Tính các giá trị lượng giác của góc 2α.

Hướng dẫn giải

Do $\frac{\pi }{2}<\alpha <\pi$ ⇒ cos α < 0.

Ta có: ${\cos }^2\alpha =1-{\sin }^2\alpha =\frac{8}{9}$

⇒ $\cos \alpha =-\frac{2\sqrt{2}}{3}$ (do cos α < 0).

$\tan 2\alpha =\frac{\sin 2\alpha }{\cos 2\alpha }=-\frac{4\sqrt{2}}{9}.\frac{9}{7}=-\frac{4\sqrt{2}}{7}.$

$\cot 2\alpha =\frac{1}{\tan 2\alpha }=-\frac{7\sqrt{2}}{8}.$

Bài 9. Xét tính chẵn lẻ của các hàm số sau:

a) $f\left(x\right)=\frac{x^2}{\sin x+\tan x}.$

b) f(x) = |x|.sin x.

Hướng dẫn giải

⇔ sin 2x ≠ 0 ⇔ 2x ≠ kπ ⇔ $x\ne \frac{k\pi }{2}$, k ∈ ℤ.

Vậy hàm số f(x) xác định trên D = ℝ \ {$\frac{k\pi }{2}$, k ∈ ℤ}. là tập đối xứng.

Vậy hàm số $f\left(x\right)=\frac{x^2}{\sin x+\tan x}$ là hàm số lẻ.

b) Hàm số f(x) xác định trên D = ℝ là tập đối xứng

Ta có: f(−x) = |−x|.sin (−x) = |x|.sin x = −f(x).

Vậy hàm số f(x) = |x|.sin x là hàm số lẻ.

Bài 10. Tìm tập xác định của hàm số: $y=\sqrt{\frac{1+\cos x}{1-\cos x}}.$

Hướng dẫn giải

⇒ $\frac{1+\cos x}{1-\cos x}\ge 0,\left(1-\cos x\right)\ne 0.$

Do đó y xác định khi và chỉ khi $1-\cos x\ne 0$ ⇔ cos x ≠ 1 ⇔ x ≠ k2π.

Vậy tập xác định của hàm số là D = ℝ \ {k2π, k ∈ ℤ}.

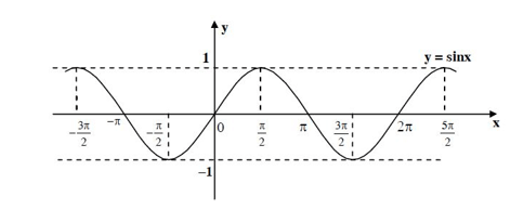
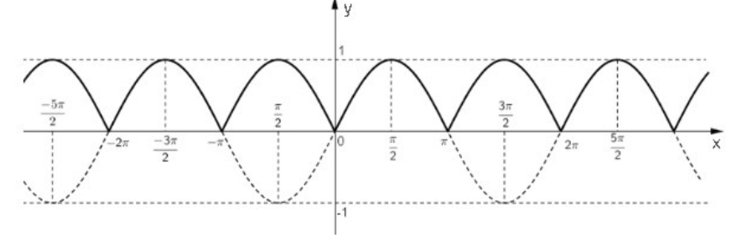
Bài 11. Dựa vào đồ thị của hàm số y = sin x, vẽ đồ thị của hàm số y = |sin x|.

Hướng dẫn giải

Ta biết đồ thị hàm số y = sin x có dạng như sau:

Với hàm số y = |sin x| ta có:

Từ dồ thị hàm số y = sin x ta có thể suy ra đồ thị hàm số y = |sin x| bằng cách:

- Giữ nguyên phần đồ thị nằm phía trên trục Ox (sin x > 0).

- Lấy đối xứng phần đồ thị nằm phía dưới Ox qua Ox.

Như vậy, ta được đồ thị hàm số y = |sin x| có dạng như sau (nét liền).

Bài 12. Giải các phương trình lượng giác sau:

a) 2sin²x + 2sinx.cosx – 5cos²x = 0

b) $\sqrt{3}\sin x-\cos x=\sqrt{2}$

Hướng dẫn giải

a) $2si{n}^{2}x+2\sin x.\cos x-5co{s}^2\text{x}=0$

⇔ $2{\tan }^{2}x+3\tan x-5=0$

Vậy phương trình đã cho có nghiệm là $x=\frac{\pi }{4}+k\pi$ hoặc $x\approx 1,2+k\pi$ (k ∈ ℤ).

b) $\sqrt{3}\sin x-\cos x=\sqrt{2}$

⇔ $\frac{\sqrt{3}}{2}\sin x-\frac{1}{2}\cos x=\frac{\sqrt{2}}{2}$

⇔ $\sin x.\cos \frac{\pi }{6}-\cos x.\sin \frac{\pi }{6}=\frac{\sqrt{2}}{2}$

⇔ $\sin \left(x-\frac{\pi }{6}\right)=\sin \frac{\pi }{4}$

Vậy phương trình đã cho có nghiệm là $x=\frac{5\pi }{12}+2k\pi$ hoặc $x=\frac{11\pi }{12}+2k\pi$ (k ∈ ℤ).

Bài 13. Giải phương trình: cos3x.tan5x = sin7x.

Hướng dẫn giải

Điều kiện cos 5x ≠ 0

Khi đó phương trình đã cho trở thành

2sin5x.cos3x = 2sin7x.cos5x

⇔ sin8x = sin12x

• Với $x=\frac{k\pi }{2}$ thì ta có:

⇔ k = 2m (m ∈ ℤ)

• Với $x=\frac{\pi }{20}+\frac{k\pi }{10}$ thì ta có:

 Vậy phương trình đã cho có nghiệm là $x=m\pi ;x=\frac{\pi }{20}+\frac{k\pi }{10}$ (m, k ∈ ℤ).

Bài 14. Tìm x ∈ [0; 14] sao cho: cos3x – 4cos2x + 3cos x – 4 = 0. (1)

Hướng dẫn giải

Ta có: cos3x = 4cos³x – 3cosx

(1) ⇔ cos3x + 3cos x – 4(1 + cos2x) = 0

⇔ 4cos³x – 8cos²x = 0

⇔ 4cos³x.(cos x – 2) = 0

⇔ cos x = 0

⇔ $x=\frac{\pi }{2}+k\pi$ (k ∈ ℤ)

Vì x ∈ [0; 14] ⇒ {$x\in \left\{\frac{\pi }{2};\frac{3\pi }{2};\frac{5\pi }{2};\frac{7\pi }{2}\right\}\}.$

Vậy {$x\in \left\{\frac{\pi }{2};\frac{3\pi }{2};\frac{5\pi }{2};\frac{7\pi }{2}\right\}\}.$

Xem thêm các bài tóm tắt lý thuyết Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 4: Hàm số lượng giác và đồ thị

Lý thuyết Bài 5: Phương trình lượng giác cơ bản

Lý thuyết Bài 1: Dãy số

Lý thuyết Bài 2: Cấp số cộng

Lý thuyết Bài 3: Cấp số nhân