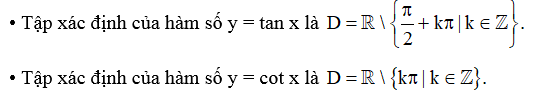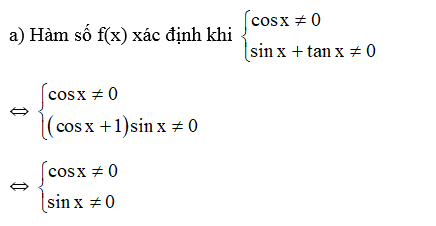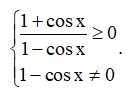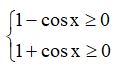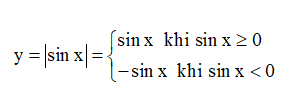Lý thuyết Toán 11 Bài 4: Hàm số lượng giác và đồ thị (Chân trời sáng tạo)

Lý thuyết Toán 11 Bài 4: Hàm số lượng giác và đồ thị

I. Lý thuyết

1. Hàm số lượng giác

- Hàm số sin là quy tắc đặt tương ứng mỗi số thực x với số thực sin x, kí hiệu y = sin x.

- Hàm số côsin là quy tắc đặt tương ứng mỗi số thực x với số thực cos x, kí hiệu          y = cos x.

- Hàm số tang là hàm số được xác định bởi công thức

$y=\frac{\sin x}{\cos x}$ với $x\ne \frac{\pi }{2}+k\pi \text{\hspace{0.17em}\hspace{0.17em}(}\left(k\in \mathbb{Z}\right)),$ kí hiệu y = tan x.

- Hàm số côtang là hàm số được xác định bởi công thức

$y=\frac{\cos x}{\sin x}$ với x ≠ kπ (k ∈ ℤ), kí hiệu y = cot x.

Chú ý:

• Tập xác định của hàm số y = sin x và y = cos x là ℝ.

2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

2.1. Hàm số chẵn, hàm số lẻ

- Hàm số y = f(x) với tập xác định D được gọi là hàm số chẵn nếu với mọi x ∈ D ta có    – x ∈ D và f(−x) = f(x).

- Hàm số y = f(x) với tập xác định D được gọi là hàm số lẻ nếu với mọi x ∈ D ta có              – x ∈ D và f(−x) = −f(x).

Chú ý:

• Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.

• Đồ thị của hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.

Ví dụ: Xét tính chẵn lẻ của hàm số y = f(x) = sin(2x + 1).

Ta có hàm số y = f(x) = sin(2x + 1) có tập xác định là ℝ. Với mọi x ∈ ℝ ta có –x ∈ ℝ và f(–x) = sin[2(–x) + 1] = sin(–2x + 1) = –sin(2x – 1).

Nhận thấy f(–x) ≠ f(x) và f(–x) ≠ –f(x).

Vậy hàm số y = sin(2x + 1) không phải hàm số chẵn, không phải hàm số lẻ.

2.2. Hàm số tuần hoàn

- Hàm số y = f(x) với tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại một số T khác 0 sao cho với mọi x ∈ D ta có x ± T ∈ D và f(x + T) = f(x).

- Số T dương nhỏ nhất thỏa mãn các điều kiện trên (nếu có) được gọi là chu kì của hàm số tuần hoàn y = f(x).

Chú ý:

• Đồ thị của hàm số tuần hoàn chu kì T được lặp lại trên từng đoạn giá trị của x có độ dài T.

• Các hàm số y = sin x và y = cos x là các hàm số tuần hoàn với chu kì 2π.

• Các hàm số y = tan x và y = cot x là các hàm số tuần hoàn với chu kì π.

3. Đồ thị của các hàm số lượng giác

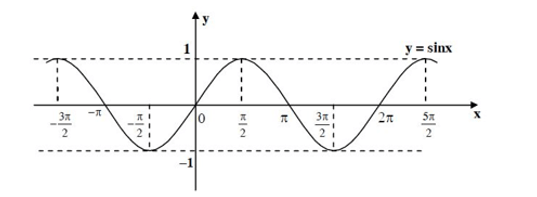
3.1. Hàm số y = sin x

Hàm số y = sin x có tập xác định là ℝ, tập giá trị là [−1; 1] và có các tính chất sau:

- Hàm số tuần hoàn với chu kì 2π.

- Hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O.

- Hàm số đồng biến trên các khoảng ($\left(-\frac{\pi }{2}+2k\pi ;\frac{\pi }{2}+2k\pi \right)\text{\hspace{0.17em}\hspace{0.17em})(}\left(k\in \mathbb{Z}\right)$) và nghịch biến trên các khoảng ($\left(\frac{\pi }{2}+2k\pi ;\frac{3\pi }{2}+2k\pi \right)\text{\hspace{0.17em}\hspace{0.17em})(}\left(k\in \mathbb{Z}\right).$)

Đồ thị của hàm số y = sin x trên ℝ như sau:

Chú ý:

• Vì y = sin x là hàm số lẻ nên để vẽ đồ thị của nó trên đoạn [−π; π], ta có thể vẽ trên đoạn [0; π], sau đó lấy đối xứng qua gốc tọa độ.

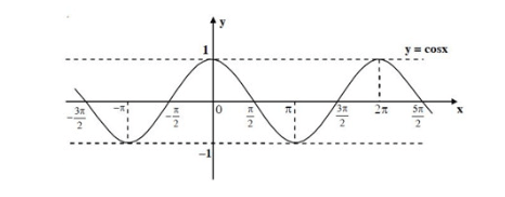
3.2. Hàm số y = cos x

Hàm số y = cos x có tập xác định là ℝ, tập giá trị là [−1; 1] và có các tính chất sau:

- Hàm số tuần hoàn với chu kì 2π.

- Hàm số chẵn, có đồ thị đối xứng qua trục Oy.

- Hàm số đồng biến trên các khoảng ($\left(-\pi +2k\pi ;2k\pi \right)\text{\hspace{0.17em}\hspace{0.17em})(}\left(k\in \mathbb{Z}\right)$) và nghịch biến trên các khoảng ($\left(2k\pi ;\pi +2k\pi \right)\text{\hspace{0.17em}\hspace{0.17em})(}\left(k\in \mathbb{Z}\right).$)

Đồ thị của hàm số y = cos x trên ℝ như sau:

Chú ý:

• Vì y = cos x là hàm số chẵn nên để vẽ đồ thị của nó trên đoạn [−π; π], ta có thể vẽ trên đoạn [0; π], sau đó lấy đối xứng qua trục tung.

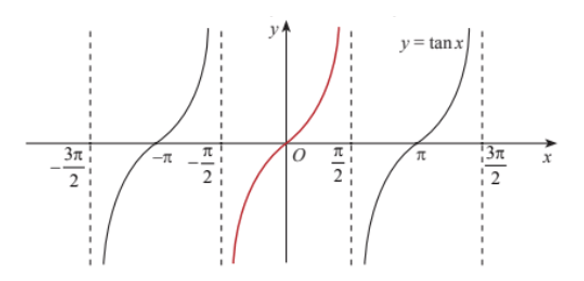
3.3. Hàm số y = tan x

Hàm số y = tan x có tập xác định là 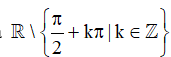 và có các tính chất sau:

- Hàm số tuần hoàn với chu kì π.

- Hàm số lẻn, có đồ thị đối xứng qua gốc tọa độ O.

- Hàm số đồng biến trên các khoảng ($\left(-\frac{\pi }{2}+k\pi ;\frac{\pi }{2}+k\pi \right)\left(k\in \mathbb{Z}\right).$)

Đồ thị của hàm số y = tan x trên 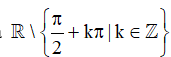 như sau:

Chú ý:

• Vì y = tan x là hàm số lẻ nên để vẽ đồ thị của nó trên khoảng ($\left(-\frac{\pi }{2};\frac{\pi }{2}\right),$) ta có thể vẽ trên nửa khoảng [$\left[0;\frac{\pi }{2}\right),$) sau đó lấy đối xứng qua gốc tọa độ.

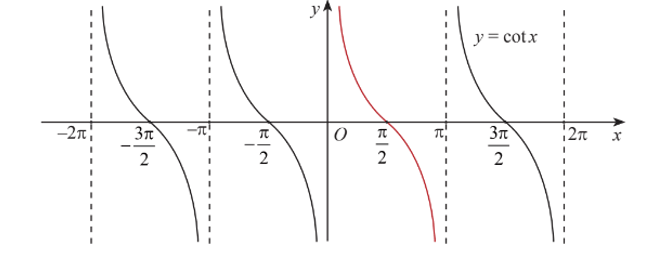
3.4. Hàm số y = cot x

Hàm số y = cot x có tập xác định là 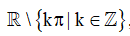 và có các tính chất sau:

- Hàm số tuần hoàn với chu kì π.

- Hàm số lẻn, có đồ thị đối xứng qua gốc tọa độ O.

- Hàm số nghịch biến trên các khoảng ($\left(k\pi ;\pi +k\pi \right)\text{\hspace{0.17em}\hspace{0.17em})(}\left(k\in \mathbb{Z}\right).$)

Đồ thị của hàm số y = cot x trên 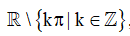 như sau:

II. Bài tập Hàm số lượng giác và đồ thị

Bài 1. Xét tính chẵn lẻ của các hàm số sau:

a) $f\left(x\right)=\frac{x^2}{\sin x+\tan x}.$

b) f(x) = |x|.sin x.

Hướng dẫn giải

⇔ sin 2x ≠ 0 ⇔ 2x ≠ kπ ⇔ $x\ne \frac{k\pi }{2}$, k ∈ ℤ.

Vậy hàm số f(x) xác định trên 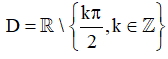 là tập đối xứng.

Ta có: $f\left(-x\right)=\frac{{\left(-x\right)}^2}{\sin \left(-x\right)+\tan \left(-x\right)}=-\frac{x^2}{\sin x+\tan x}=-f\left(x\right)$

Vậy hàm số $f\left(x\right)=\frac{x^2}{\sin x+\tan x}$ là hàm số lẻ.

b) Hàm số f(x) xác định trên D = ℝ là tập đối xứng

Ta có: f(−x) = |−x|.sin (−x) = |x|.sin x = −f(x).

Vậy hàm số f(x) = |x|.sin x là hàm số lẻ.

Bài 2. Tìm tập xác định của hàm số: $y=\sqrt{\frac{1+\cos x}{1-\cos x}}.$

Hướng dẫn giải

Hàm số $y=\sqrt{\frac{1+\cos x}{1-\cos x}}$ xác định ⇔

Vì $-1\le \cos x\le 1,\forall x\in ℝ$ nên 

⇒ $\frac{1+\cos x}{1-\cos x}\ge 0,\left(1-\cos x\right)\ne 0.$

Do đó y xác định khi và chỉ khi $1-\cos x\ne 0$ ⇔ cos x ≠ 1 ⇔ x ≠ k2π.

Vậy tập xác định của hàm số là D = ℝ \ {k2π, k ∈ ℤ}.

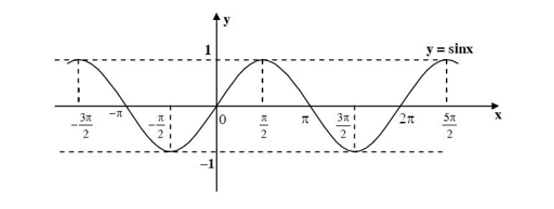
Bài 3. Dựa vào đồ thị của hàm số y = sin x, vẽ đồ thị của hàm số y = |sin x|.

Hướng dẫn giải

Ta biết đồ thị hàm số y = sin x có dạng như sau:

Với hàm số y = |sin x| ta có:

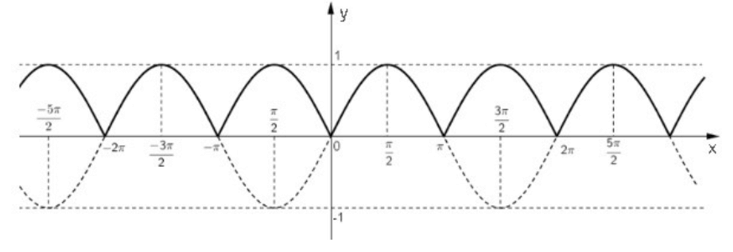
Từ dồ thị hàm số y = sin x ta có thể suy ra đồ thị hàm số y = |sin x| bằng cách:

- Giữ nguyên phần đồ thị nằm phía trên trục Ox (sin x > 0).

- Lấy đối xứng phần đồ thị nằm phía dưới Ox qua Ox.

Như vậy, ta được đồ thị hàm số y = |sin x| có dạng như sau (nét liền).

Xem thêm các bài tóm tắt lý thuyết Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 2: Giá trị lượng giác của một góc lượng giác

Lý thuyết Bài 3: Các công thức lượng giác

Lý thuyết Bài 5: Phương trình lượng giác cơ bản

Tổng hợp lý thuyết Toán 11 Chương 1

Lý thuyết Bài 1: Dãy số