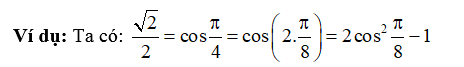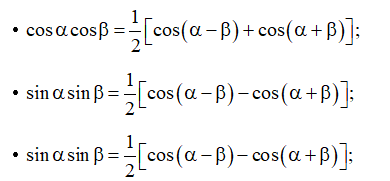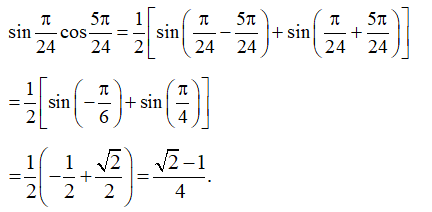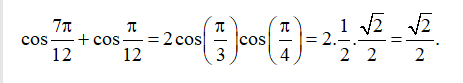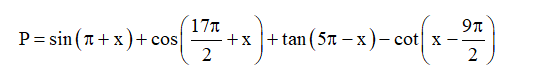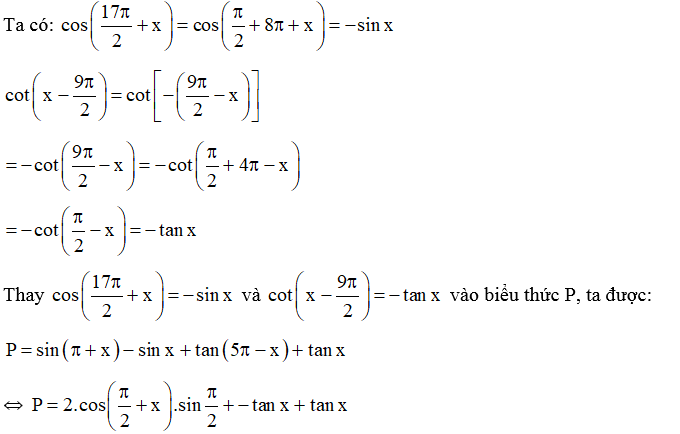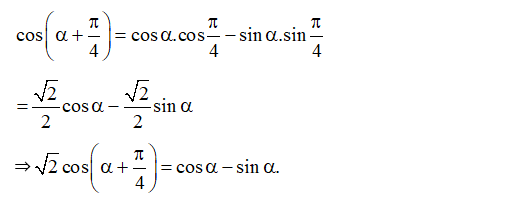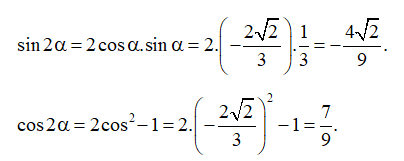Lý thuyết Toán 11 Bài 3: Các công thức lượng giác (Chân trời sáng tạo)

Lý thuyết Toán 11 Bài 3: Các công thức lượng giác

I. Lý thuyết

1. Công thức cộng

• cos(α + β) = cosα.cosβ – sinα.sinβ;            

• cos(α – β) = cosα.cosβ + sinα.sinβ;

• sin(α + β) = sinα.cosβ + cosα.sinβ;             

• sin(α – β) = sinα.cosβ − cosα.sinβ;

• $\mathrm{tan(}\left(\alpha +\beta \right))=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta };$                      

• $\mathrm{tan(}\left(\alpha -\beta \right))=\frac{\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }.$

$=\sin \frac{\pi }{2}\cos \frac{\pi }{3}-\cos \frac{\pi }{2}\sin \frac{\pi }{3}$

$=1.\frac{1}{2}-0.\frac{\sqrt{3}}{2}=\frac{1}{2}.$

2. Công thức góc nhân đôi

- Công thức góc nhân đôi là công thức tính các giá trị lượng giác của góc 2α qua các giá trị lượng giác của góc α.

- Công thức góc nhân đôi bao gồm những công thức sau:

• cos2α = cos²α – sin²α = 2cos²α – 1 = 1 – 2sin²α;

• sin2α = 2sinα . cosα;

• $\tan 2\alpha =\frac{2\tan \alpha }{1-{\tan }^2\alpha }.$

⇒ ${\cos }^2\frac{\pi }{8}=\frac{2+\sqrt{2}}{4}.$

Vì $0<\frac{\pi }{8}<\frac{\pi }{2}$ nên $\cos \frac{\pi }{8}>0\Rightarrow \cos \frac{\pi }{8}=\frac{\sqrt{2+\sqrt{2}}}{2}.$

3. Công thức biến đổi tích thành tổng

Ví dụ:

4. Công thức biến đổi tổng thành tích

• $\cos \alpha +\cos \beta =2\cos \frac{\alpha +\beta }{2}\cos \frac{\alpha -\beta }{2};$       

• $\cos \alpha -\cos \beta =-2\sin \frac{\alpha +\beta }{2}\sin \frac{\alpha -\beta }{2};$

• $\sin \alpha +\sin \beta =2\sin \frac{\alpha +\beta }{2}\cos \frac{\alpha -\beta }{2};$          

• $\sin \alpha -\sin \beta =2\cos \frac{\alpha +\beta }{2}\sin \frac{\alpha -\beta }{2}.$

Ví dụ:

II. Bài tập Các công thức lượng giác

Bài 1. Rút gọn biểu thức sau:

Hướng dẫn giải

⇔ $P=-2\sin x$

Vậy P = −2sin x.

Bài 2. Chứng minh rằng: $\cos \alpha -\sin \alpha =\sqrt{2}\mathrm{cos(}\left(\alpha +\frac{\pi }{4}\right)).$

Hướng dẫn giải

Ta có:

Bài 3. Cho $\sin \alpha =\frac{1}{3}$ và $\frac{\pi }{2}<\alpha <\pi .$ Tính các giá trị lượng giác của góc 2α.

Hướng dẫn giải

Do $\frac{\pi }{2}<\alpha <\pi$ ⇒ cos α < 0.

Ta có: ${\cos }^2\alpha =1-{\sin }^2\alpha =\frac{8}{9}$

⇒ $\cos \alpha =-\frac{2\sqrt{2}}{3}$ (do cos α < 0).

$\tan 2\alpha =\frac{\sin 2\alpha }{\cos 2\alpha }=-\frac{4\sqrt{2}}{9}.\frac{9}{7}=-\frac{4\sqrt{2}}{7}.$

$\cot 2\alpha =\frac{1}{\tan 2\alpha }=-\frac{7\sqrt{2}}{8}.$

Xem thêm các bài tóm tắt lý thuyết Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 1: Góc lượng giác

Lý thuyết Bài 2: Giá trị lượng giác của một góc lượng giác

Lý thuyết Bài 4: Hàm số lượng giác và đồ thị

Lý thuyết Bài 5: Phương trình lượng giác cơ bản

Tổng hợp lý thuyết Toán 11 Chương 1