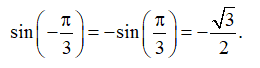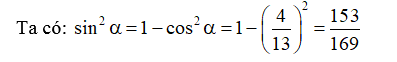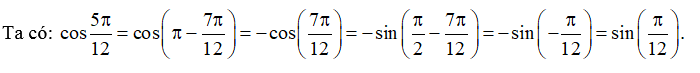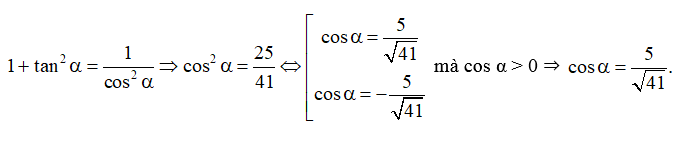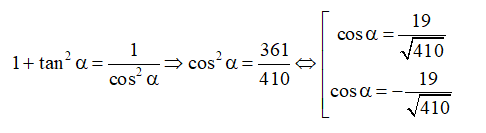Lý thuyết Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác
I. Lý thuyết
1. Giá trị lượng giác của góc lượng giác
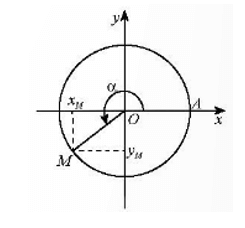
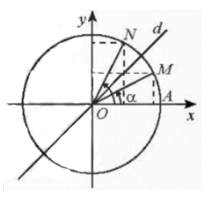
- Trên đường tròn lượng giác, gọi M là điểm biểu diễn góc lượng giác có số đo α. Khi đó:
• Tung độ yM của M gọi là sin của α, kí hiệu sin α.
• Hoành độ xM của M gọi là côsin của α, kí hiệu cos α.
• Nếu xM ≠ 0 thì tỉ số gọi là tang của α, kí hiệu tan α.
• Nếu yM ≠ 0 thì tỉ số gọi là côtang của α, kí hiệu cot α.
Các giá trị sin α, cos α, tan α và cot α được gọi là các giá trị lượng giác của góc lượng giác α.
Chú ý:
• Ta gọi trục hoành là trục côsin, còn trục tung là trục sin.
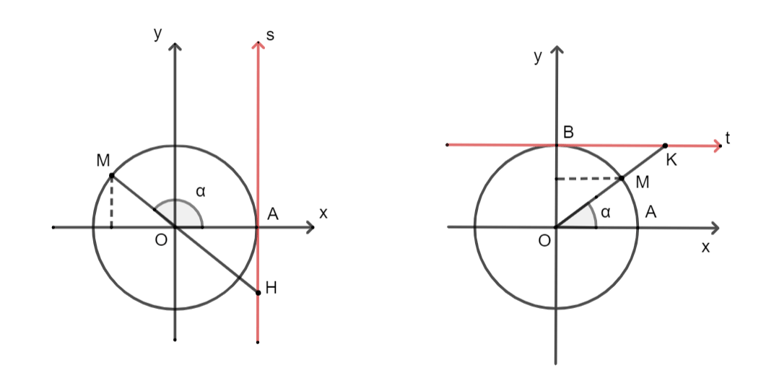
• Trục As có gốc ở điểm A(1; 0) và song song với trục sin gọi là trục tang. Nếu đường thẳng OM cắt trục tang thì tung độ của giao điểm đó chính là tan α.
• Trục Bt có gốc ở điểm B(0; 1) và song song với trục côsin gọi là trục côtang. Nếu đường thẳng OM cắt trục côtang thì hoành độ của giao điểm đó chính là cot α.
• sin α và cos α xác định với mọi α ∈ ℝ;
tan α chỉ xác định với các góc
cot α chỉ xác định với các góc α ≠ kπ (k ∈ ℤ).
• Với mọi góc lượng giác α và số nguyên k, ta có:
sin(α + k2π) = sin α; tan(α + kπ) = tan α;
cos(α + k2π) = cos α; cot(α + kπ) = cot α.
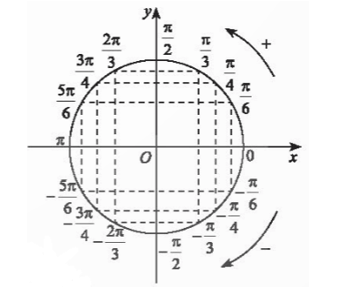
• Ta có thể sử dụng đường tròn lượng giác để xác định giá trị lượng giác của góc α.
Ví dụ: Theo đường tròn lượng giác, ta thấy điểm biểu diễn của góc và góc đối xứng nhau qua trục hoành, nên chúng có cùng hoành độ và tung độ đối nhau. Do đó ta có:
2. Tính giá trị lượng giác của một góc bằng máy tính cầm tay
Giá trị lượng giác của một góc bất kỳ có thể tính bằng máy tính cầm tay.
Chú ý:
• Trước khi tính, cần chọn đơn vị đo góc bằng cách:
+ Ấn các phím SHIFT, MENU và 2 để màn hình hiện lên bảng lựa chọn đơn vị đo góc bao gồm: Degree, Radian và Gradian.
+ Tiếp tục ấn phím 1 để chọn đơn vị độ (Degree) hoặc phím 2 để chọn đơn vị radian (Radian).
+ Cuối cùng ấn phím MENU và 1 để vào chế độ tính toán.
3. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác
Ta có những hệ thức sau liên hệ giữa các giá trị lượng giác của cùng một góc lượng giác α:
• sin2α + cos2α = 1
• tan α . cot α = 1 với k ∈ ℤ
• với k ∈ ℤ
• với α ≠ kπ, k ∈ ℤ
Ví dụ: Cho ):
mà
.
.
4. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt
4.1. Hai góc đối nhau: 𝛂 và –𝛂
|
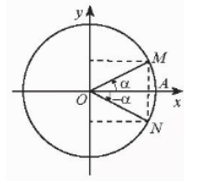
Các điểm biểu diễn của hai góc α và –α đối xứng qua trục Ox nên ta có: • sin(–α) = −sin α; • cos(–α) = cos α; • tan(–α) = −tan α; • cot(–α) = −cot α. |
|
4.2. Hai góc hơn kém nhau 𝛑: 𝛂 và 𝛂 + 𝛑
|
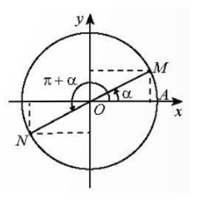
Các điểm biểu diễn của hai góc α và α + π đối xứng nhau qua gốc tọa độ O nên ta có: • sin(α + π) = −sin α; • cos(α + π) = −cos α; • tan(α + π) = tan α; • cot(α + π) = cot α. |
|
4.3. Hai góc bù nhau: 𝛂 và 𝛑 – 𝛂
|
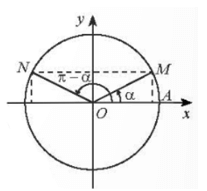
Các điểm biểu diễn của hai góc α và π – α đối xứng nhau qua trục Oy nên ta có: • sin(π – α) = sin α; • cos(π – α) = −cos α; • tan(π – α) = −tan α; • cot(π – α) = −cot α. |
|
4.4. Hai góc phụ nhau: 𝛂 và
|
Các điểm biểu diễn của hai góc α và đối xứng nhau qua đường phân giác d của góc xOy nên ta có: • • • • |
|
Ví dụ: Biểu diễn qua giá trị lượng giác của góc có số đo từ 0 đến
II. Bài tập Giá trị lượng giác của một góc lượng giác
Bài 1. Tính các giá trị lượng giác của góc α biết:
a) biết
b) biết
Hướng dẫn giải
a) Do nên sin α < 0, cos α > 0, cot α < 0.
Ta có:
b) Do nên sin α > 0, cos α < 0, tan α < 0.
Ta có:
Mà cos α < 0 ⇒
Bài 2. Rút gọn các biểu thức sau:
a) A = (1 – sin2α).cot2α + 1 – cot2α;
b) .
Hướng dẫn giải
a) A = (1 – sin2α).cot2α + 1 – cot2α
⇔ A = cot2α – sin2α.cot2α + 1 – cot2α
⇔
b)
⇔
⇔ B = cos α – sin α.
Bài 3. Cho Tính:
Hướng dẫn giải
Chia cả tử và mẫu của biểu thức A cho cos2α ta được:
Xem thêm các bài tóm tắt lý thuyết Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 1: Góc lượng giác
Lý thuyết Bài 3: Các công thức lượng giác
Lý thuyết Bài 4: Hàm số lượng giác và đồ thị