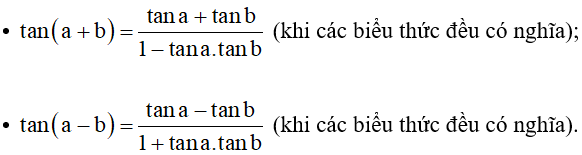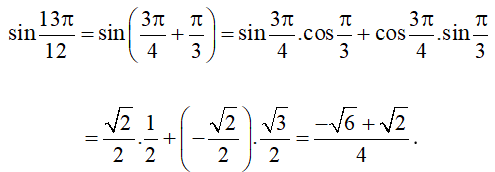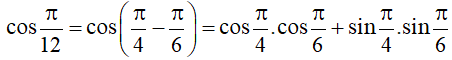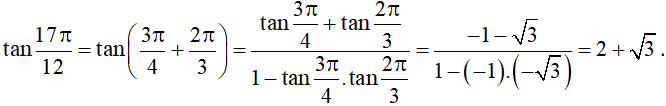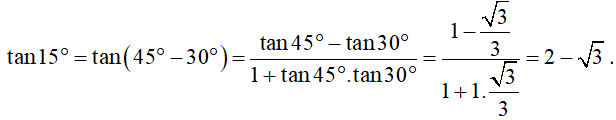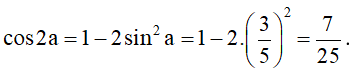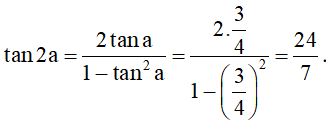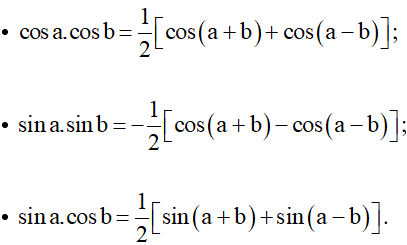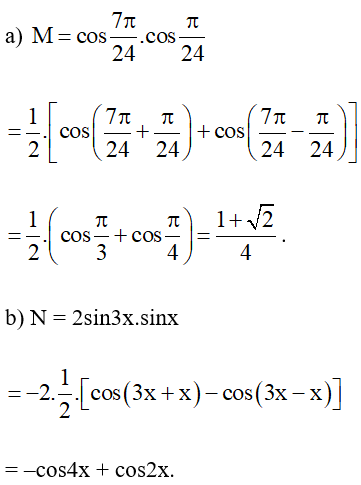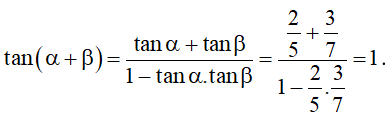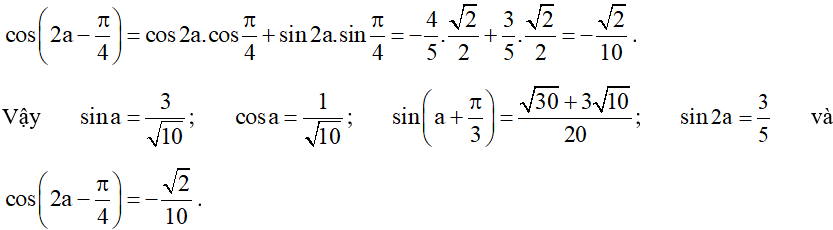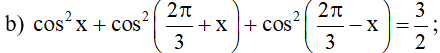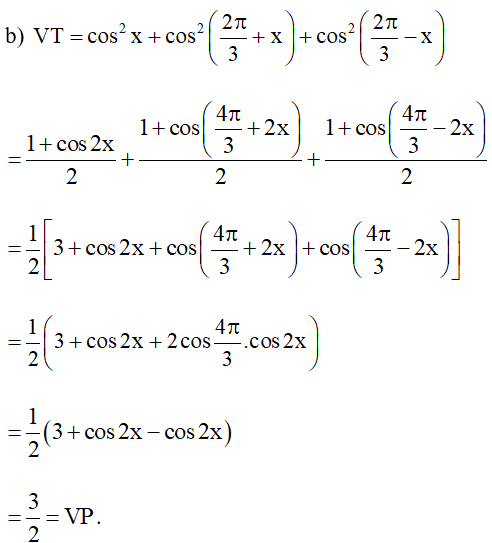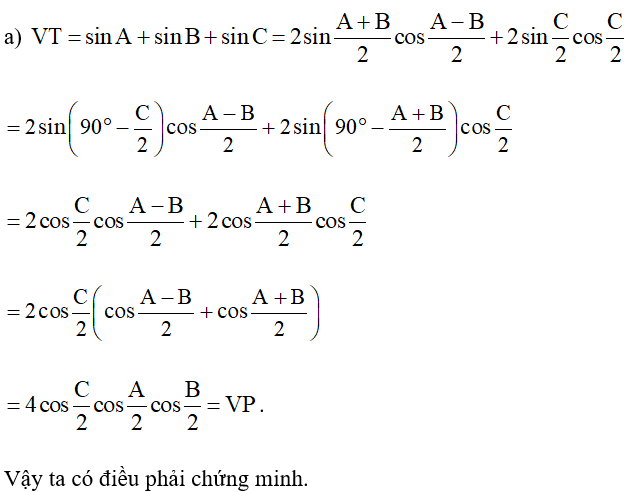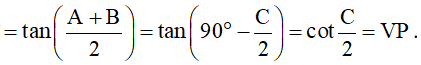Lý thuyết Toán 11 Bài 2: Các phép biến đổi lượng giác (Cánh diều)

Lý thuyết Toán 11 Bài 2: Các phép biến đổi lượng giác

1. Công thức cộng

Công thức cộng:

⦁ sin(a + b) = sina.cosb + cosa.sinb;

⦁ sin(a – b) = sina.cosb – cosa.sinb.

⦁ cos(a + b) = cosa.cosb – sina.sinb;

⦁ cos(a – b) = cosa.cosb + sina.sinb.

Ví dụ 1. Tính:

a) $\sin \frac{13\pi }{12}$;

b) sin15°.

c) cos105°;

d) $\cos \frac{\pi }{12}$.

Hướng dẫn giải

a) Áp dụng công thức cộng đối với sin, ta được:

Vậy $\sin \frac{13\pi }{12}=\frac{-\sqrt{6}+\sqrt{2}}{4}$.

b) Áp dụng công thức cộng đối với sin, ta được:

sin15° = sin(60° – 45°) = sin60°.cos45° – cos60°.sin45°

           $=\frac{\sqrt{3}}{2}.\frac{\sqrt{2}}{2}-\frac{1}{2}.\frac{\sqrt{2}}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}$.

Vậy $\sin 15°=\frac{\sqrt{6}-\sqrt{2}}{4}$.

c) Áp dụng công thức cộng đối với côsin, ta được:

cos105° = cos(60° + 45°) = cos60°.cos45° – sin60°.sin45°

             $=\frac{1}{2}.\frac{\sqrt{2}}{2}-\frac{\sqrt{3}}{2}.\frac{\sqrt{2}}{2}=\frac{-\sqrt{6}+\sqrt{2}}{4}$.

Vậy $\cos 105°=\frac{-\sqrt{6}+\sqrt{2}}{4}$.

d) Áp dụng công thức cộng đối với côsin, ta được:

           $=\frac{\sqrt{2}}{2}.\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}.\frac{1}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}$.

Vậy $\cos \frac{\pi }{12}=\frac{\sqrt{6}+\sqrt{2}}{4}$.

Ví dụ 2. Tính:

a) $\tan \frac{17\pi }{12}$;

b) tan15°.

Hướng dẫn giải

a) Áp dụng công thức cộng đối với tang, ta được:

Vậy $\tan \frac{17\pi }{12}=2+\sqrt{3}$.

b) Áp dụng công thức cộng đối với tang, ta được:

Vậy $\tan 15°=2-\sqrt{3}$.

2. Công thức nhân đôi

Công thức nhân đôi:

⦁ sin2a = 2sina.cosa;

⦁ cos2a = cos²a – sin²a;

⦁ $\tan 2a=\frac{2\tan a}{1-{\tan }^{2}a}$ (khi các biểu thức đều có nghĩa).

Nhận xét:

⦁ cos2a = cos²a – sin²a = 2cos²a – 1 = 1 – 2sin²a;

⦁ ${\cos }^{2}a=\frac{1+\cos 2a}{2};{\sin }^{2}a=\frac{1-\cos 2a}{2}$ (thường gọi là công thức hạ bậc).

Ví dụ 3. Cho $\sin a=\frac{3}{5}$ và $0<a<\frac{\pi }{2}$. Tính cos2a, cosa, sin2a, tan2a.

Hướng dẫn giải

• Áp dụng công thức nhân đôi, ta được:

• Vì $0<a<\frac{\pi }{2}$ nên cosa > 0.

Áp dụng công thức hạ bậc, ta được:

${\cos }^{2}a=\frac{1+\cos 2a}{2}=\frac{1+\frac{7}{25}}{2}=\frac{16}{25}$ $\iff \cos a=\frac{4}{5}$.

• Áp dụng công thức nhân đôi, ta được:

$\sin 2a=2\sin a.\cos a=2.\frac{3}{5}.\frac{4}{5}=\frac{24}{25}$.

Ta có $\tan a=\frac{\sin a}{\cos a}=\frac{3}{5}:\frac{4}{5}=\frac{3}{4}$.

• Áp dụng công thức nhân đôi, ta được:

Vậy $\cos 2a=\frac{7}{25}$; $\cos a=\frac{4}{5}$; $\sin 2a=\frac{24}{25}$ và $\tan 2a=\frac{24}{7}$.

3. Công thức biến đổi tích thành tổng

Công thức biến đổi tích thành tổng:

Ví dụ 4. Biến đổi các tích sau thành tổng:

a) $M=\cos \frac{7\pi }{24}.\cos \frac{\pi }{24}$;

b) N = 2sin3x.sinx.

Hướng dẫn giải

4. Công thức biến đổi tổng thành tích

Công thức biến đổi tổng thành tích:

⦁ $\cos u+\cos v=2.\cos \frac{u+v}{2}.\cos \frac{u-v}{2}$;

⦁ $\cos u-\cos v=-2.\sin \frac{u+v}{2}.\sin \frac{u-v}{2}$;

⦁ $\sin u+\sin v=2.\sin \frac{u+v}{2}.\cos \frac{u-v}{2}$;

⦁ $\sin u-\sin v=2.\cos \frac{u+v}{2}.\sin \frac{u-v}{2}$.

Ví dụ 5. Tính:

a) P = sinx + sin9x;

b) $Q=\frac{\cos 75°+\cos 15°}{\cos 75°-\cos 15°}$.

Hướng dẫn giải

a) P = sinx + sin9x =  sin9x + sinx

$=2\sin \frac{9x+x}{2}.\cos \frac{9x-x}{2}$

= 2sin5x.cos4x.

b) $Q=\frac{\cos 75°+\cos 15°}{\cos 75°-\cos 15°}$.

$=\frac{2\cos \frac{75°+15°}{2}.\cos \frac{75°-15°}{2}}{-2\sin \frac{75°+15°}{2}.\sin \frac{75°-15°}{2}}$

$=\frac{\cos 45°.\cos 30°}{-\sin 45°.\sin 30°}$

= –cot45°.cot30°

$=-\sqrt{3}$.

Bài tập Các phép biến đổi lượng giác

Bài 1. Tính α + β biết $\tan \alpha =\frac{2}{5},\tan \beta =\frac{3}{7}$.

Hướng dẫn giải

Áp dụng công thức cộng đối với tang, ta được: 

Vậy $\alpha +\beta =\frac{\pi }{4}$.

Bài 2. Cho $\cos 2a=-\frac{4}{5}$, với $\frac{\pi }{4}<a<\frac{\pi }{2}$. Tính sina, cosa, , sin2a, .

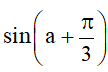
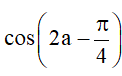
Hướng dẫn giải

Vì $\frac{\pi }{4}<a<\frac{\pi }{2}$ nên sina > 0, cosa > 0.

• Áp dụng công thức hạ bậc, ta được: ${\sin }^{2}a=\frac{1-\cos 2a}{2}=\frac{1+\frac{4}{5}}{2}=\frac{9}{10}$

Suy ra $\sin a=\frac{3}{\sqrt{10}}$ (do sina > 0)

• Áp dụng công thức hạ bậc, ta được: ${\cos }^{2}a=\frac{1+\cos 2a}{2}=\frac{1-\frac{4}{5}}{2}=\frac{1}{10}$.

Suy ra $\cos a=\frac{1}{\sqrt{10}}$.

• Áp dụng công thức cộng đối với sin, ta được:

$=\frac{3}{\sqrt{10}}.\frac{1}{2}+\frac{1}{\sqrt{10}}.\frac{\sqrt{3}}{2}=\frac{\sqrt{30}+3\sqrt{10}}{20}$.

• Áp dụng công thức nhân đôi, ta được:

$\sin 2a=2\sin a\cos a=2.\frac{3}{\sqrt{10}}.\frac{1}{\sqrt{10}}=\frac{3}{5}$.

• Áp dụng công thức cộng đối với côsin, ta được:

Bài 3. Chứng minh rằng:

a) ${\cos }^{3}x.\sin x-{\sin }^{3}x.\cos x=\frac{1}{4}\sin 4x$;

Hướng dẫn giải

a) VT = cos³x.sinx – sin³x.cosx

= cosx.sinx.(cos²x – sin²x)

$=\frac{1}{2}\sin 2x.\cos 2x$

$=\frac{1}{4}\sin 4x$ = VP.

Vậy ta có điều phải chứng minh.

Bài 4. Cho ∆ABC. Chứng minh rằng:

a) $\sin A+\sin B+\sin C=4\cos \frac{A}{2}\cos \frac{B}{2}\cos \frac{C}{2}$;

b) $\frac{\sin A+\sin B}{\cos A+\cos B}=\cot \frac{C}{2}$;

c) $\sin 2A+\sin 2B+\sin 2C=\frac{2S}{R^2}$, với R là bán kính đường tròn ngoại tiếp ∆ABC và S là diện tích ∆ABC.

Hướng dẫn giải

∆ABC, có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$, suy ra $\widehat{A}+\widehat{B}=180°-\widehat{C}$

Do đó $\frac{\widehat{A}+\widehat{B}}{2}=90°-\frac{\widehat{C}}{2}$.

b) $VT=\frac{\sin A+\sin B}{\cos A+\cos B}=\frac{2\sin \frac{A+B}{2}\cos \frac{A-B}{2}}{2\cos \frac{A+B}{2}\cos \frac{A-B}{2}}$

Vậy ta có điều phải chứng minh.

c) VT = sin2A + sin2B + sin2C

= 2sin(A + B).cos(A – B) + 2sinC.cosC

= 2sin(180° – C).cos(A – B) + 2sinC.cosC

= 2sinC.cos(A – B) + 2sinC.cosC

= 2sinC.[cos(A – B) + cosC]

= 2sinC.[cos(A – B) + cos(180° – A – B)]

= 2sinC.[cos(A – B) – cos(A + B)]

= –4sinC.sinA.sin(–B)

= 4sinA.sinB.sinC

$=4.\frac{a}{2R}.\frac{b}{2R}.\frac{c}{2R}=\frac{abc}{4R}.\frac{2}{R^2}=\frac{2S}{R^2}=VP$.

Vậy ta có điều phải chứng minh.

Xem thêm các bài tóm tắt lý thuyết Toán 11 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác

Lý thuyết Bài 3: Hàm số lượng giác và đồ thị

Lý thuyết Bài 4: Phương trình lượng giác cơ bản

Tổng hợp lý thuyết Toán 11 Chương 1

Lý thuyết Bài 1: Dãy số