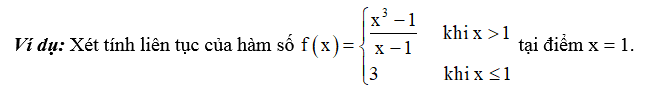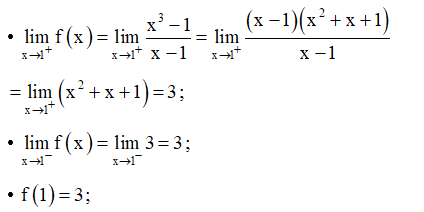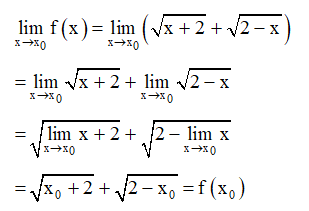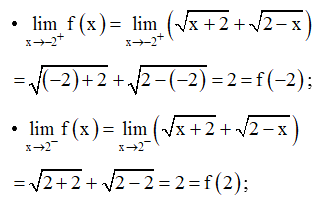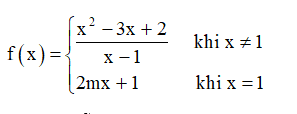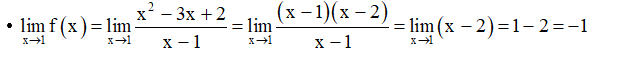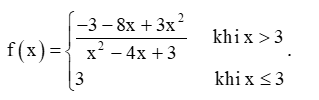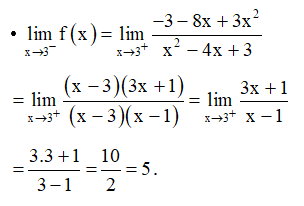Lý thuyết Toán 11 Bài 3: Hàm số liên tục (Chân trời sáng tạo)

Lý thuyết Toán 11 Bài 3: Hàm số liên tục

I. Lý thuyết

1. Hàm số liên tục tại một điểm

Cho hàm số y = f(x) xác định trên khoảng K và x₀ $\in$ K.

Hàm số y = f(x) được gọi là liên tục tại điểm x₀ nếu$\underset{x\to x_0}{\lim }$f(x) = f(x₀) .

Nhận xét: Để hàm số y = f(x) liên tục tại x₀ thì phải có cả ba điều sau:

• Hàm số xác định tại x₀;

• Tồn tại $\underset{x\to x_0}{\lim }$f(x) ;

• $\underset{x\to x_0}{\lim }$ f(x) = f(x₀) .

Chú ý: Khi hàm số y = f(x) không liên tục tại điểm x₀ thì ta nói f (x) gián đoạn tại điểm  x₀ và x₀ được gọi là điểm gián đoạn của hàm số f (x).

Hướng dẫn giải

Ta có:

Vì $\underset{x\to 1^{+}}{\lim }$f(x) = $\underset{x\to 1^{-}}{\lim }$f(x) = f(1)nên hàm số trên liên tục tại điểm x = 1.

2. Hàm số liên tục trên một khoảng, trên một đoạn

• Cho hàm số y = f(x) xác định trên khoảng (a; b).

Hàm số y = f(x) được gọi là liên tục trên khoảng (a; b) nếu f(x) liên tục tại mọi điểm trong khoảng ấy.

• Cho hàm số y = f(x) xác định trên đoạn [a; b].

Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu f(x) liên tục trên khoảng (a; b) và $\underset{x\to a^{+}}{\lim }$f(x) = f(a), $\underset{x\to b^{-}}{\lim }$f(x) = f(b).

Nhận xét: Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) < 0 thì luôn tồn tại ít nhất một điểm c $\in$ (a; b) sao cho f (c) = 0.

Ví dụ: Xét tính liên tục của hàm số $y=\sqrt{x+2}+\sqrt{2-x}$  trên [−2; 2].

Hướng dẫn giải

Với mọi  $x_0\in$(-2; 2), ta có:

Do đó f (x) liên tục tại mọi điểm $x_0\in$(-2; 2)

Ta lại có:

Vậy hàm số $y=\sqrt{x+2}+\sqrt{2-x}$  liên tục trên đoạn [−2; 2].

3. Tính liên tục của hàm số sơ cấp

• Hàm số đa thức y = P (x)  , các hàm số lượng giác y = sin x, y = cos x liên tục trên ℝ.

• Hàm số phân thức y = $\frac{P \left(x\right)}{Q \left(x\right)}$, hàm số căn thức y = $\sqrt{P\left(x\right)}$, các hàm số lượng giác $y=\tan x,y=\cot x$  liên tục trên các khoảng của tập xác định của chúng.

Trong đó P(x) và Q(x) là các đa thức.

Nhận xét: Hàm số thuộc những loại trên được gọi chung là hàm số sơ cấp.

Sau đây, khi nói xét tính liên tục của một hàm số mà không nói gì thêm thì ta xét tính liên tục của hàm số đó trên những khoảng xác định của nó.

Ví dụ: Xét tính liên tục của các hàm số sau:

a) y = 2x³ + 3x² – 2;

b) $y=\frac{x^2+x+1}{x-2}$ .

Hướng dẫn giải

a) y = 2x³ + 3x² – 2 là hàm số đa thức nên nó liên tục trên ℝ.

b) $y=\frac{x^2+x+1}{x-2}$  là hàm số phân thức, có tập xác định (–∞; 2) ∪ (2; +∞) nên nó liên tục trên các khoảng (–∞; 2) và (2; +∞).

4. Tổng, hiệu, tích, thương của hàm số liên tục

Cho hai hàm số số y = f(x) và y = g(x) liên tục tại điểm x₀. Khi đó:

• Các hàm số y = f(x) + g(x); y = f(x) – g(x) và y = f(x).g(x) liên tục tại x₀.

• Hàm số y = $\frac{f\left(x\right)}{g\left(x\right)}$ liên tục tại x₀ nếu g(x₀) ≠ 0.

Ví dụ: Xét tính liên tục của hàm số $y=\frac{x-2}{\sqrt{x-4}}$ .

Hướng dẫn giải

Tập xác định của hàm số: D = (4; +∞).

Các hàm số y = x – 2 và $y=\sqrt{x-4}$  liên tục tại mọi điểm x₀ ∈ D.

Do đó, hàm số $y=\frac{x-2}{\sqrt{x-4}}$  liên tục trên khoảng (4; +∞).

II. Bài tập Hàm số liên tục

Bài 1. Tìm giá trị m để hàm số sau đây liên tục trên tập xác định:

Hướng dẫn giải

Tập xác định của hàm số là D = ℝ.

Xét trường hợp x ≠ 1, hàm số có dạng f(x) = $\frac{x^2-3x+2}{x-1}$, là hàm số phân thức trên tập xác định (–∞; 1) ∪ (1; +∞) nên nó liên tục trên các khoảng (–∞; 1) và (1; +∞).

Xét trường hợp x = 1, ta có:

• f(1) = 2m. 1+1= 2m +1

Khi đó, để hàm f (x) liên tục tại điểm x₀ = 1 thì:

$\underset{x\to 1}{\lim }$f(x) = f(1)$\iff$2m+1= -1$\iff$m = - 1

Vậy m = −1 là giá trị của tham số m cần tìm.

Bài 2. Xét tính liên tục của hàm số sau đây tại điểm x = 3.

Hướng dẫn giải

Ta có:

• $\underset{x\to 3^{+}}{\lim }$f(x) = $\underset{x\to 3^{+}}{\lim }$3 = 3

Do $\underset{x\to 3^{+}}{\lim }$f(x) $\ne$ $\underset{x\to 3^{-}}{\lim }$f(x) (3 $\ne$5) nên hàm số gián đoạn tại điểm x = 3.

Bài 3. Chứng minh rằng phương trình 3x³ + x² – x – 1 có nghiệm trong khoảng (−1; 1).

Hướng dẫn giải

Hàm số f(x) = 3x³ + x² – x – 1 là một hàm số đa thức, nên f (x) liên tục trên ℝ.

Suy ra, f (x) cũng liên tục trên đoạn [−1; 1].

Ta có:

• f(–1) = 3 . (–1)³ + (–1)² – (–1) – 1 = –3 + 1 + 1 – 1 = –2;

• f(1) = 3 . 1³ + 1² – 1 – 1 = 3 + 1 – 1 – 1 = 2.

Suy ra f(–1) . f(1) = (–2) . 2 = – 4 < 0.

Do vậy, có ít nhất một nghiệm c $\in$ (−1; 1) sao cho f (c) = 0.

Vậy phương trình 3x³ + x² – x – 1 có nghiệm trong khoảng (−1; 1).

Xem thêm các bài tóm tắt lý thuyết Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 1: Giới hạn của dãy số

Lý thuyết Bài 2: Giới hạn của hàm số

Tổng hợp lý thuyết Toán 11 Chương 3

Lý thuyết Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian

Lý thuyết Bài 2: Hai đường thẳng song song