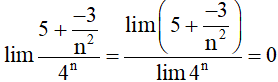Lý thuyết Toán 11 Bài 1: Giới hạn của dãy số (Cánh diều)

Lý thuyết Toán 11 Bài 1: Giới hạn của dãy số

1. Giới hạn hữu hạn của dãy số

1.1. Định nghĩa

– Dãy số (u_n) có giới hạn 0 khi n dần tới dương vô cực nếu |u_n| có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi, kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=0$.

– Dãy số (u_n) có giới hạn hữu hạn là a khi n dần tới dương vô cực nếu 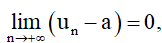 kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=a$.

Nhận xét: Nếu u_n càng ngày càng gần tới 0 khi n ngày càng lớn thì lim u_n = 0.

Chú ý:

– Ngoài kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=0$, ta cũng sử dụng kí hiệu sau:

lim u_n = 0 hay u_n → 0 khi n → +∞.

– Ngoài kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=\mathrm{a}$, ta cũng sử dụng kí hiệu sau:

lim u_n = a hay u_n → a khi n → +∞.

– Một dãy số có giới hạn thì giới hạn đó là duy nhất.

– Không phải dãy số nào cũng có giới hạn, chẳng hạn như dãy số (u_n) với u_n = (–1)ⁿ.

Ví dụ 1. Chứng minh $\lim \frac{2n+1}{n}=2$.

Hướng dẫn giải

Vì 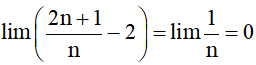 nên $\lim \frac{2n+1}{n}=2$.

2. Một số giới hạn cơ bản

Ta thừa nhận các giới hạn sau:

a) $\lim \frac{1}{n}=0$; $\lim \frac{1}{n^k}=0$ với k là số nguyên dương cho trước;

b) $\lim \frac{c}{n}=0$; $\lim \frac{\mathrm{c}}{n^k}=0$ với c là hằng số, k là số nguyên dương cho trước;

c) Nếu |q| < 1 thì lim qⁿ = 0;

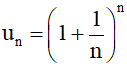
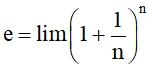
d) Dãy số (u_n) với có giới hạn là một số vô tỉ và gọi giới hạn đó là e,

.

Một giá trị gần đúng của e là 2,718281828459045.

Ví dụ 2. Chứng minh .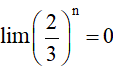

Hướng dẫn giải

.

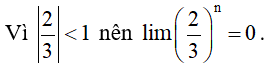
2. Định lí về giới hạn hữu hạn

a) Nếu lim u_n = a,  lim v_n = b thì:

lim (u_n + v_n) = a + b;

lim (u_n – v_n) = a – b;

lim (u_n . v_n) = a . b;

.

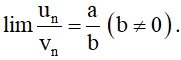
b) Nếu u_n ≥ 0 với mọi n và lim u_n = a thì a ≥ 0 và $\lim \sqrt{u_n}=\sqrt{a}$.

Ví dụ 3. Tính giới hạn của dãy số:

.

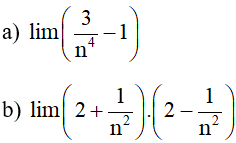
Hướng dẫn giải

.

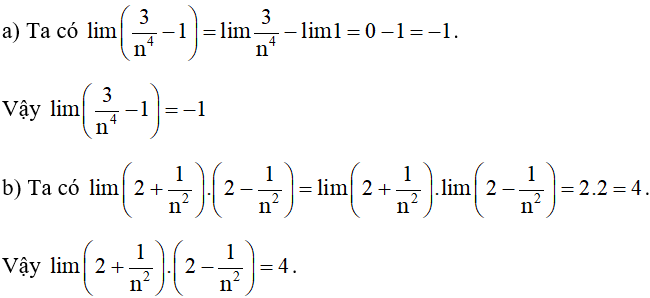
3. Tổng của cấp số nhân lùi vô hạn

Cấp số nhân vô hạn u₁, u₁q, …., u₁q^{n – 1}, … có công bội q thỏa mãn |q| < 1 được gọi là cấp số nhân lùi vô hạn.

Tổng của cấp số nhân lùi vô hạn đã cho là:

$S=u_1+u_{1}q+\mathrm{....}+u_1{q}^{n-1}+\mathrm{...}=\frac{u_1}{1-q}$.

Ví dụ 4. Tính tổng $S=\frac{1}{3}+\frac{1}{3^2}+\mathrm{...}+\frac{1}{3^n}+\mathrm{...}$

Hướng dẫn giải

Các số hạng của tổng trên lập thành một cấp số nhân (u_n), có $u_1=\frac{1}{3}$, công bội $q=\frac{1}{3}$.

Suy ra $S=\frac{1}{3}+\frac{1}{3^2}+\mathrm{...}+\frac{1}{3^n}+\mathrm{...}=\frac{\frac{1}{3}}{1-\frac{1}{3}}=\frac{1}{2}$.

Vậy $S=\frac{1}{2}$.

4. Giới hạn vô cực

Định nghĩa dãy số có giới hạn vô cực:

– Ta nói dãy số (u_n) có giới hạn + ∞ khi n dần tới dương vô cực, nếu u_n có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.

Kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=+\infty$ hay $\lim u_n=+\infty$ hay u_n → + ∞ khi n → + ∞.

– Ta nói dãy số (u_n) có giới hạn –∞ khi n dần tới dương vô cực, nếu .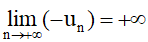

Kí hiệu $\underset{n\to +\infty }{\lim }{u}_n=-\infty$ hay $\lim u_n=-\infty$ hay u_n → – ∞ khi n → + ∞.

Nhận xét:

• lim n^k = + ∞ với k là số nguyên dương cho trước.

• lim qⁿ = + ∞ với q > 1 là số thực cho trước.

• Nếu lim u_n = a và lim |v_n| = + ∞  thì $\lim \frac{u_n}{v_n}=0$.

• Nếu lim u_n = a, a > 0 và lim v_n = 0, v_n > 0 với mọi n  thì $\lim \frac{u_n}{v_n}=+\infty$.

• lim u_n = +∞ ⇔ lim (–u_n) = –∞.

Ví dụ 5. Chứng tỏ rằng .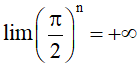

Hướng dẫn giải

Vì $\fra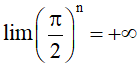c{\pi }{2}>1$ nên .

Bài tập Giới hạn của dãy số

Bài 1. Tính các giới hạn sau:

a) $\lim \frac{3}{5n-2}$;

b) $\lim \frac{-4n+6}{2n}$;

c) $\lim \frac{4^n+{6.2}^n}{{3.4}^n}$;

d) $\lim \frac{5+\frac{-3}{n^2}}{4^n}$.

Hướng dẫn giải

a) Ta có .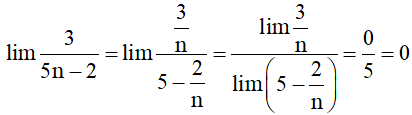

Vậy $\lim \frac{3}{5n-2}=0$.

b) Ta có .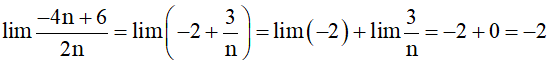

Vậy $\lim \frac{-4n+6}{2n}=-2$.

.

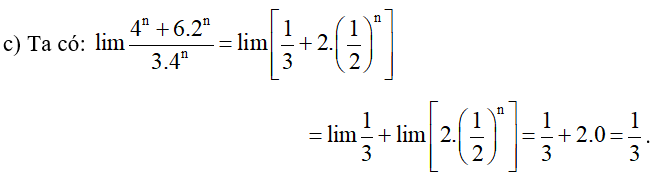
Vậy $\lim \frac{4^n+{6.2}^n}{{3.4}^n}=\frac{1}{3}$.

d) Ta có: 

Vậy $\lim \frac{5+\frac{-3}{n^2}}{4^n}=0$.

Bài 2. Cho $u_n=\frac{1}{n^3}+2$ và $v_n=1-\frac{1}{n}$. Tính các giới hạn:

lim (u_n + v_n); lim(u_n – v_n); lim(u_n.v_n);  $\lim \frac{u_n}{v_n}$.

Hướng dẫn giải

.

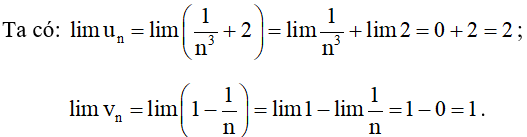
Khi đó:

• lim (u_n + v_n) = lim u_n + lim v_n = 2 + 1 = 3.

• lim (u_n – v_n) = lim u_n – lim v_n = 2 – 1 = 1.

• lim (u_n . v_n) = lim u_n . lim v_n = 2 . 1 = 2

• $\lim \frac{u_n}{v_n}=\frac{\lim u_n}{\lim v_n}=\frac{2}{1}=2$.

Bài 3. Tính tổng của cấp số nhân lùi vô hạn biết u₁ = 1, công bội $q=\frac{2}{3}$.

Hướng dẫn giải

Tổng của cấp số nhân lùi vô hạn với u₁ = 1, công bội $q=\frac{2}{3}$ là:

  $S=u_1+u_{1}q+\mathrm{...}+u_1{q}^{n-1}+\mathrm{...}=\frac{1}{1-\frac{2}{3}}=3$.

Vậy S = 3.

Xem thêm các bài tóm tắt lý thuyết Toán 11 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 3: Cấp số nhân

Tổng hợp lý thuyết Toán 11 Chương 2

Lý thuyết Bài 2: Giới hạn của hàm số

Lý thuyết Bài 3: Hàm số liên tục

Tổng hợp lý thuyết Toán 11 Chương 3