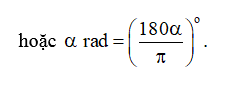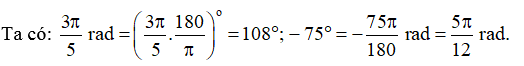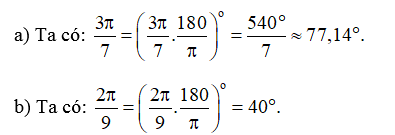Lý thuyết Toán 11 Bài 1: Góc lượng giác (Chân trời sáng tạo)

Lý thuyết Toán 11 Bài 1: Góc lượng giác

I. Lý thuyết

1. Góc lượng giác

1.1. Khái niệm

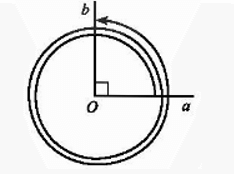
Cho hai tia Oa, Ob:

- Nếu một tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob, kí hiệu (Oa, Ob) = α.

- Khi tia Om quay một góc α, ta nói số đo của góc lượng giác (Oa, Ob) bằng α, kí hiệu sđ(Oa, Ob) = α.

- Số đo của các góc lượng giác có cùng tia đầu Oa và tia cuối Ob khác nhau một bội nguyên của 360° nên có công thức tổng quát là:

sđ(Oa, Ob) = α° + k . 360° (k ∈ ℤ), thường viết là (Oa, Ob) = α° + k . 360°

với α° là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.

Chú ý:

• Với hai tia Oa và Ob cho trước, có vô số góc lượng giác tia đầu Oa và tia cuối Ob. Ta dùng chung kí hiệu (Oa, Ob) cho tất cả các góc lượng giác này.

Ví dụ: Cho góc lượng giác (Oa, Ob).

Ta viết: số đo của góc lượng giác (Oa, Ob) là 90° + 2 . 360° = 810°.

1.2. Hệ thức Chasles (Sa – lơ)

Với ba tia Oa, Ob và Oc bất kì, ta có:

(Oa, Ob) + (Ob, Oc) = (Oa, Oc) + k . 360° (k ∈ ℤ).

2. Đơn vị radian

- Trên đường tròn bán kính R tùy ý, góc ở tâm chắn một cung có độ dài đúng bằng R được gọi là một góc có số đo 1 radian (đọc là 1 ra – đi – an, viết tắt là 1 rad).

- Công thức chuyển đổi số đo góc từ đơn vị radian sang độ và ngược lại như sau:

$\alpha °=\frac{\pi \alpha }{180}rad$

Ví dụ:

Chú ý:

• Khi ghi số đo của một góc theo đơn vị radian, người ta thường bỏ đi chữ rad sau số đo. Ví dụ, $\frac{\pi }{2}rad$ được viết là $\frac{\pi }{2}$, 2 rad được viết là 2.

• Với đơn vị radian, công thức số đo tổng quát của một góc lượng giác (Oa, Ob) là

(Oa, Ob) = α + k2$\pi$ (k ∈ ℤ),

trong đó α là số đo theo radian của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob. Lưu ý không được viết α + k.360° hay α° + k2$\pi$ (vì không cùng đơn vị đo).

3. Đường tròn lượng giác

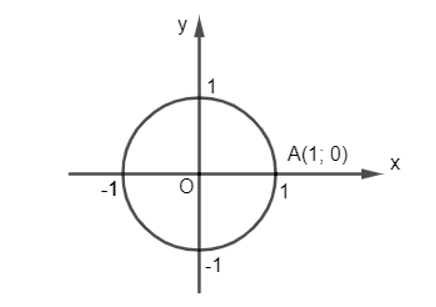
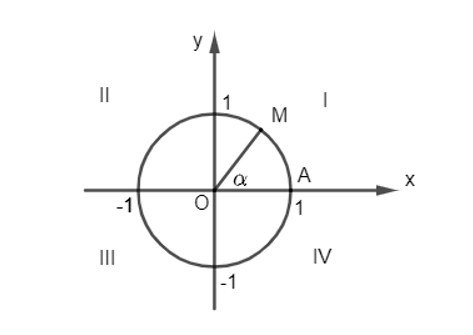
- Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm O bán kính bằng 1. Trên đường tròn này, chọn điểm A(1; 0) làm gốc, chiều dương là chiều ngược chiều kim đồng hồ và chiều âm là chiều cùng chiều kim đồng hồ. Đường tròn cùng với gốc và chiều như trên được gọi là đường tròn lượng giác.

- Cho số đo góc α bất kì. Trên đường tròn lượng giác, ta xác định được duy nhất một điểm M sao cho số đo góc lượng giác (OA, OM) bằng α. Khi đó M được gọi là điểm biểu diễn của góc có số đo α trên đường tròn lượng giác.

Chú ý:

• Hệ trục tọa độ Oxy chia mặt phẳng tọa độ thành bốn “góc phần tư” kí hiệu lần lượt là I, II, III và IV.

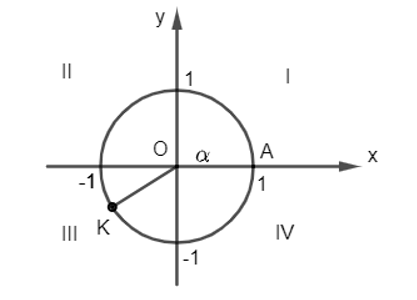
Ví dụ: Biểu diễn trên đường tròn lượng giác góc lượng giác có số đo $\frac{9\pi }{7}.$

Ta có: $\frac{9\pi }{7}=\frac{2\pi }{7}+\pi .$ 

Vậy điểm biểu diễn góc lượng giác có số đo $\frac{9\pi }{7}$ là điểm K trên phần đường tròn lượng giác thuộc góc phần tư thứ III sao cho $\widehat{AOK}=\pi -\frac{2\pi }{7}=\frac{5\pi }{7}.$

II. Bài tập Góc lượng giác

Bài 1. Đổi số đo của các góc sau đây sang radian:

a) −125°;

b) 42°;

Hướng dẫn giải

a) Ta có: $-125°=\frac{\pi .(-125)}{180}rad=-\frac{25\pi }{36}rad.$

b) Ta có: $42°=\frac{42\pi }{180}rad=\frac{7\pi }{30}rad.$

Bài 2. Đổi số đo của các góc sau đây sang độ:

a) $\frac{3\pi }{7};$

b) $\frac{2\pi }{9};$

Hướng dẫn giải

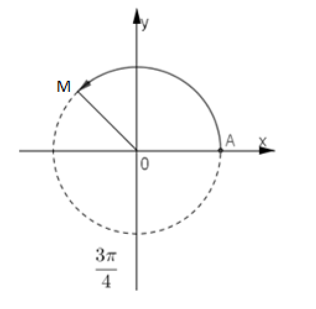
Bài 3. Biểu diễn trên đường tròn lượng giác góc lượng giác có số đo 135°:

Hướng dẫn giải

Ta có: $135°=45°+\frac{1}{4}.360°.$

Vậy điểm biểu diễn góc lượng giác có số đo 135° là điểm M nằm trên phần đường tròn lượng giác thuộc góc phần tư thứ II sao cho $\widehat{AOM}=135°.$

Xem thêm các bài tóm tắt lý thuyết Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 2: Giá trị lượng giác của một góc lượng giác

Lý thuyết Bài 3: Các công thức lượng giác

Lý thuyết Bài 4: Hàm số lượng giác và đồ thị

Lý thuyết Bài 5: Phương trình lượng giác cơ bản

Tổng hợp lý thuyết Toán 11 Chương 1