Lý thuyết Toán 11 Bài 4: Hai mặt phẳng song song (Cánh diều)

Lý thuyết Toán 11 Bài 4: Hai mặt phẳng song song

1. Hai mặt phẳng song song

Nhận xét:

Đối với hai mặt phẳng phân biệt (P) và (Q) trong không gian, có hai khả năng xảy ra:

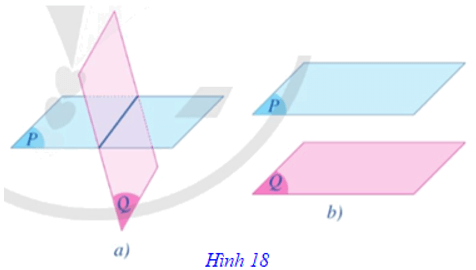
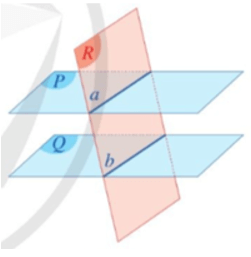
⦁ Hai mặt phẳng (P) và (Q) có điểm chung. Khi đó, chúng cắt nhau theo một đường thẳng (Hình 18a).

⦁ Hai mặt phẳng (P) và (Q) không có điểm chung. Khi đó, ta nói chúng song song với nhau, kí hiệu (P) // (Q) hay (Q) // (P) (Hình 18b).

Ta có định nghĩa sau:

Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm chung.

Trong thực tiễn có nhiều hình ảnh về hai mặt phẳng song song.

Chẳng hạn:

+ Mặt bàn và sàn nhà gợi nên hình ảnh về hai mặt phẳng song song.

+ Các mặt của giá để đồ ở Hình 58 gợi nên hình ảnh về những mặt phẳng song song.

2. Điều kiện và tính chất

Định lí 1: (Dấu hiệu nhận biết hai mặt phẳng song song)

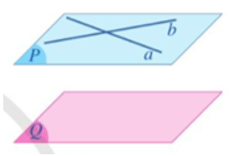
Nếu mặt phẳng (P) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q).

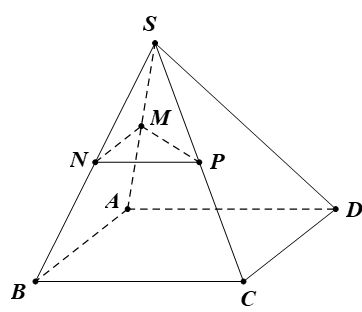
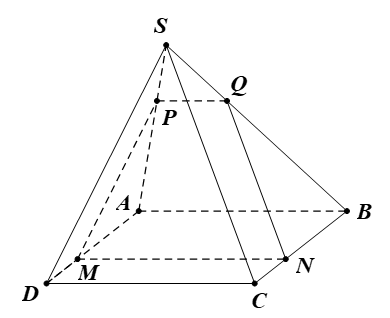
Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, SB, SC. Chứng minh (MNP) // (ABCD).

Hướng dẫn giải

Tam giác SAB có MN là đường trung bình.

Suy ra MN // AB.

Mà AB ⊂ (ABCD).

Do đó MN // (ABCD)    (1)

Chứng minh tương tự, ta được NP // (ABCD)   (2)

Trong (MNP): N = MN ∩ NP   (3)

Từ (1), (2), (3), ta thu được (MNP) // (ABCD).

Định lí 2: (Tính chất về hai mặt phẳng song song)

Qua một điểm nằm ngoài một mặt phẳng cho trước, có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.

Tức là, cho điểm M nằm ngoài mặt phẳng (Q), có duy nhất một mặt phẳng (P) chứa điểm M và song song với mặt phẳng (Q).

Từ định lí trên, ta có các hệ quả sau:

Hệ quả 1. Nếu đường thẳng a song song với mặt phẳng (Q) thì có duy nhất một mặt phẳng (P) chứa a và song song với mặt phẳng (Q).

Hệ quả 2. Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.

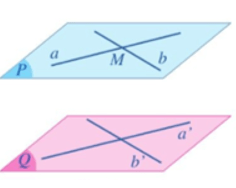
Định lí 3: Cho hai mặt phẳng song song (P) và (Q). Nếu mặt phẳng (R) cắt mặt phẳng (P) thì cũng cắt mặt phẳng (Q) và hai giao tuyến a, b của chúng song song với nhau.

Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là một điểm trên đoạn AD sao cho AM = 2DM. Mặt phẳng (α) đi qua M và song song với (SCD), cắt BC, SA, SB theo thứ tự tại N, P, Q. Chứng minh rằng MN // CD, từ đó tính tỉ số $\frac{BN}{BC}$.

Hướng dẫn giải

Ta có M, N đều thuộc hai mặt phẳng (ABCD) và (α).

Suy ra MN = (ABCD) ∩ (α)   (1)

Lại có C, D đều thuộc hai mặt phẳng (SCD) và (ABCD).

Suy ra CD = (SCD) ∩ (ABCD)   (2)

Theo đề, ta có: (SCD) // (α)   (3)

Từ (1), (2), (3), ta suy ra MN // CD.

Mà DM // CN (do tứ giác ABCD là hình bình hành).

Do đó tứ giác MNCD là hình bình hành.

Vì vậy DM = CN.

Chứng minh tương tự, ta được AM = BN.

Theo đề, ta có AM = 2DM. Suy ra BN = 2CN.

Vậy $\frac{BN}{BC}=\frac{2}{3}$.

3. Định lí Thalès

Định lí 4: (Định lí Thalès)

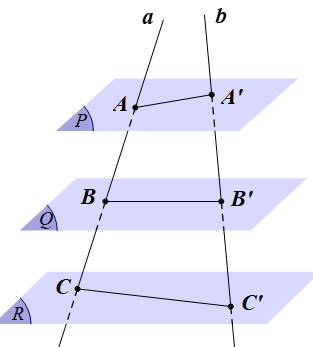
Nếu a, b là hai đường thẳng phân biệt cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A, B, C và A’, B’, C’ thì:

$\frac{AB}{A^{\text{'}}{B}^{\text{'}}}=\frac{BC}{B^{\text{'}}{C}^{\text{'}}}=\frac{CA}{C^{\text{'}}{A}^{\text{'}}}$.

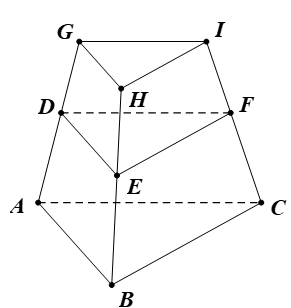
Ví dụ 3. Cho một kệ để đồ có 3 mâm (ABC), (DEF), (GHI) song song với nhau (hình vẽ). Một người thợ đo được các cạnh AG = 120 cm, BH = 144 cm, HE = 60 cm, FI = 65 cm. Tính độ dài cạnh CI của kệ để đồ.

Hướng dẫn giải

Ta có:

⦁ Đường thẳng AG cắt ba mặt phẳng song song (ABC), (DEF), (GHI) lần lượt tại A, D, G.

⦁ Đường thẳng BH cắt ba mặt phẳng song song (ABC), (DEF), (GHI) lần lượt tại B, E, H.

Áp dụng định lí Thalès trong không gian, ta được: $\frac{GD}{HE}=\frac{AG}{BH}=\frac{120}{144}=\frac{5}{6}$.

Suy ra $GD=\frac{5}{6}.HE=\frac{5}{6}.60=50$(cm).

Lại có:

⦁ Đường thẳng AG cắt ba mặt phẳng song song (ABC), (DEF), (GHI) lần lượt tại A, D, G.

⦁ Đường thẳng CI cắt ba mặt phẳng song song (ABC), (DEF), (GHI) lần lượt tại C, F, I.

Áp dụng định lí Thalès trong không gian, ta được: $\frac{AG}{CI}=\frac{GD}{FI}=\frac{50}{65}=\frac{10}{13}$.

Suy ra $CI=\frac{13}{10}.AG=\frac{13}{10}.120=156$ (cm).

Vậy CI = 156 cm.

Bài tập Hai mặt phẳng song song

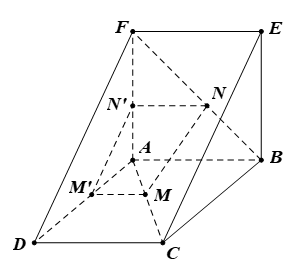
Bài 1. Cho hai hình vuông ABCD và ABEF thuộc hai mặt phẳng phân biệt. Trên các đường chéo AC và BF, lấy các điểm M, N sao cho AM = BN. Từ M, N, vẽ các đường thẳng song song với AB, lần lượt cắt AD và AF tại các điểm M’ và N’. Chứng minh:

a) (ADF) // (BCE).

b) (DEF) // (MM’N’N).

Hướng dẫn giải

a) Ta có AD // BC (do ABCD là hình vuông).

Mà BC ⊂ (BCE), suy ra AD // (BCE)   (1)

Chứng minh tương tự, ta được AF // (BCE)    (2)

Trong (ADF): AD ∩ AF = A   (3)

Từ (1), (2), (3), ta thu được (ADF) // (BCE).

b) Ta có hai hình vuông ABCD và ABEF có cùng cạnh AB.

Do đó hai hình vuông ABCD và ABEF bằng nhau.

Vì vậy hai đường chéo AC và BF bằng nhau hay AC = BF  (1)

Do MM’ // CD (giả thiết) nên áp dụng định lí Thales, ta được: $\frac{A{M}^{\text{'}}}{AD}=\frac{AM}{AC}$  (2)

Chứng minh tương tự, ta được: $\frac{A{N}^{\text{'}}}{AF}=\frac{BN}{BF}$   (3)

Lại có AM = BN (giả thiết)   (4)

Từ (1), (2), (3), (4), suy ra $\frac{A{M}^{\text{'}}}{AD}=\frac{A{N}^{\text{'}}}{AF}$.

Áp dụng định lí Thales đảo, ta được M’N’ // DF.

Mà M’N’ ⊂ (MM’N’N).

Do đó DF // (MM’N’N)  (*)

Ta có NN’ // AB (giả thiết) và AB // EF (ABEF là hình vuông).

Suy ra NN’ // EF.

Mà NN’ ⊂ (MM’N’N).

Do đó EF // (MM’N’N)  (**)

Trong (DEF): DF ∩ EF = F  (***)

Từ (*), (**), (***), ta thu được (DEF) // (MM’N’N).

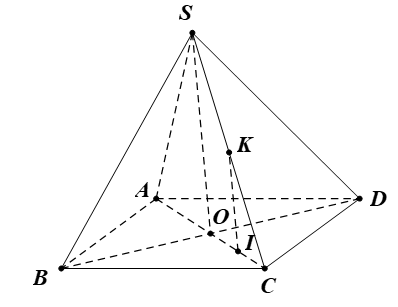
Bài 2. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Mặt phẳng (P) song song với (SBD) và đi qua điểm I thuộc đoạn OC (I ≠ O và I ≠ C). Gọi K là giao điểm của đường thẳng SC và mặt phẳng (P). Chứng minh IK // SO.

Hướng dẫn giải

Ta có K là giao điểm của đường thẳng SC và mặt phẳng (P).

Suy ra K đều thuộc hai mặt phẳng (SAC) và (P).

Mà I đều thuộc hai mặt phẳng (SAC) và (P).

Do đó KI là giao tuyến của hai mặt phẳng (SAC) và (P).

Lại có (SBD) // (P) (giả thiết) và (SAC) ∩ (SBD) = SO.

Vậy theo định lí 3, ta có IK // SO.

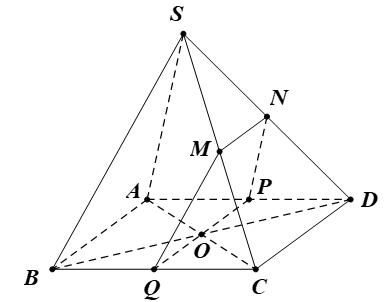
Bài 3. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi (α) là mặt phẳng đi qua O và song song với (SAB), mặt phẳng (α) cắt các đường thẳng SC, SD, AD, BC lần lượt tại các điểm M, N, P, Q. Chứng minh N là trung điểm SD.

Hướng dẫn giải

Qua điểm O, ta dựng PQ // AB, với P ∈ AD và Q ∈ BC.

Khi đó P, Q lần lượt là trung điểm của AD và BC.

Do đó CQ = BQ.

Vì tứ giác ABCD là hình bình hành nên AB // CD // PQ.

Khi đó theo Hệ quả 2 của Định lí 2, ta có duy nhất một mặt phẳng (β) chứa CD và song song với (SAB) và (α).

Ta có:

⦁ Đường thẳng CB cắt ba mặt phẳng song song (β), (α) và (SAB) lần lượt tại C, Q, B.

⦁ Đường thẳng DS cắt ba mặt phẳng song song (β), (α) và (SAB) lần lượt tại D, N, S.

Áp dụng định lí Thalès trong không gian, ta có: $\frac{QB}{NS}=\frac{CQ}{DN}$.

Suy ra $\frac{DN}{NS}=\frac{CQ}{QB}=1$.

Vậy N là trung điểm SD.

Xem thêm các bài tóm tắt lý thuyết Toán 11 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 2: Hai đường thẳng song song trong không gian

Lý thuyết Bài 3: Đường thẳng và mặt phẳng song song

Lý thuyết Bài 5: Hình lăng trụ và hình hộp

Lý thuyết Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian

Tổng hợp lý thuyết Toán 11 Chương 4