Dạng 2: Chứng minh đường thẳng song song có đáp án
-
146 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Trong hình vẽ dưới đây có bao nhiêu đoạn thẳng song song với các cạnh của tam giác ABC?
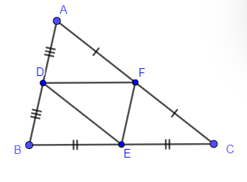
Xem đáp án
Đáp án đúng là: C
Trong tam giác ABC có:
+ D là trung điểm AB, E là trung điểm BC
Do đó DE là đường trung bình của tam giác ABC.
Suy ra DE // AC (tính chất đường trung bình của tam giác).
+ D là trung điểm AB, F là trung điểm AC
Do đó DF là đường trung bình của tam giác ABC.
Suy ra DF // BC (tính chất đường trung bình của tam giác).
+ F là trung điểm AC, E là trung điểm BC
Do đó EF là đường trung bình của tam giác ABC.
Suy ra EF // AB (tính chất đường trung bình của tam giác).
Vậy trong hình trên có 3 đoạn thẳng song song với các cạnh của tam giác ABC.
Câu 2:
Cho tam giác MNP có H, I lần lượt là trung điểm của NP và MP. Trong các khẳng định sau khẳng định nào là đúng?
Xem đáp án
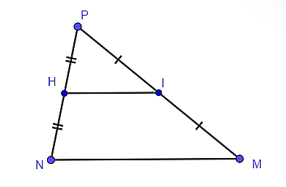
Trong tam giác MNP có H là trung điểm của NP, I là trung điểm của MP.
Do đó HI là đường trung bình của tam giác MNP.
Suy ra HI // MN (tính chất đường trung bình của tam giác).
Vậy A đúng.
Câu 3:
Quan sát hình vẽ và cho biết MG song song với đoạn thẳng nào?
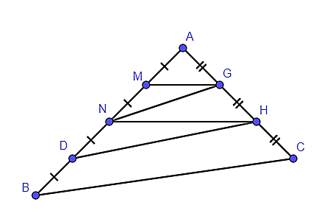
Xem đáp án
Đáp án đúng là: D
Trong tam giác AHN có M là trung điểm của AN, G là trung điểm của AH.
Do đó MG là đường trung bình của tam giác AHN.
Suy ra MG // HN (tính chất đường trung bình của tam giác).
Câu 4:
Cho tam giác ABC, các đường trung tuyến AM, BN cắt nhau tại G. Gọi I và K lần lượt là trung điểm của GA và GB. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: C
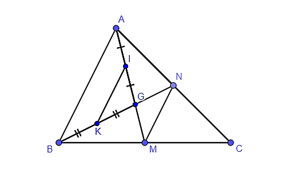
Vì AM, BN là các đường trung tuyến của tam giác ABC nên M là trung điểm của BC và N là trung điểm của AC.
Trong tam giác ABC có M là trung điểm của BC, N là trung điểm của AC.
Do đó MN là đường trung bình của tam giác ABC.
Suy ra MN // AB và (tính chất đường trung bình của tam giác) (1).
Trong tam giác GAB có I là trung điểm của GA, K là trung điểm của GB.
Do đó IK là đường trung bình của tam giác GAB.
Suy ra IK // AB và (tính chất đường trung bình của tam giác) (2).
Từ (1) và (2) suy ra IK // MN và IK = MN.
Câu 5:
Cho tam giác ABC cân tại A có trung tuyến AM. Từ M kẻ tia Mx song song với AB cắt AC tại F, kẻ My song song với AC cắt AB tại E. Khẳng định nào sau đây là sai?
Xem đáp án
Đáp án đúng là: B
Có AM là đường trung tuyến nên M là trung điểm BC.
Trong tam giác ABC có
+ M là trung điểm BC, ME // AC, E ∈ AB.
Do đó E là trung điểm AB (tính chất đường trung bình của tam giác) (1).
+ M là trung điểm BC, MF // AB, F ∈ AC.
Do đó F là trung điểm AC (tính chất đường trung bình của tam giác) (2).
Từ (1) và (2) suy ra EF là đường trung bình của tam giác ABC.
Suy ra EF // BC và .
Suy ra EF // BM và (vì M là trung điểm BC).
Vậy B sai.
Câu 6:
Cho tam giác ABC có D, E lần lượt là trung điểm của AB, AC. Khẳng định nào sau đây là sai?
Xem đáp án
Đáp án đúng là: A
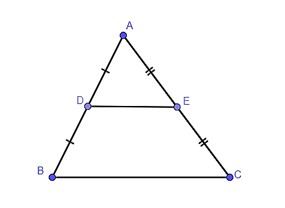
Trong tam giác ABC có D là trung điểm AB, E lần lượt là trung điểm của AC.
Do đó DE là đường trung bình của tam giác ABC.
Suy ra DE // BC và (tính chất đường trung bình của tam giác).
Vậy B, C, D đúng và A sai do mới khẳng định được DECB là hình thang, hình thang này là hình thang cân nếu có thêm điều kiện tam giác ABC cân tại A.
Câu 7:
Cho hình vẽ, khẳng định nào sau đây là sai?
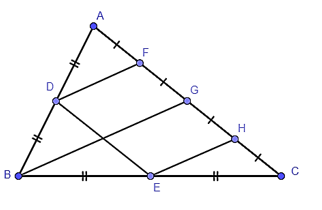
Xem đáp án
Đáp án đúng là: C
Trong tam giác ABG có D là trung điểm AB, F là trung điểm AG.
Do đó DF là đường trung bình của tam giác ABG.
Suy ra DF // BG (tính chất đường trung bình của tam giác) (1).
Trong tam giác CBG có H là trung điểm CG, E là trung điểm CB.
Do đó HE là đường trung bình của tam giác CBG.
Suy ra HE // BG (tính chất đường trung bình của tam giác) (2).
Từ (1) và (2) suy ra DF // HE // BG.
Vậy C sai.
Câu 8:
Cho tam giác ABC vuông tại B và D, E, F lần lượt là trung điểm của AC, BC, AB. Tứ giác BFDE là hình gì?
Xem đáp án
Đáp án đúng là: D
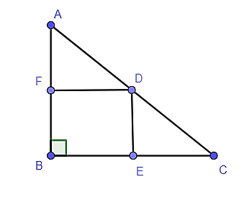
Trong tam giác ABC có
+ D là trung điểm của AC, F là trung điểm của AB.
Do đó FD là đường trung bình của tam giác ABC.
Suy ra FD // BC hay FD // BE (E ∈ BC) (tính chất đường trung bình của tam giác).
+ D là trung điểm của AC, E là trung điểm của BC.
Do đó DE là đường trung bình của tam giác ABC.
Suy ra DE // AB hay DE // BF (F ∈ AB) (tính chất đường trung bình của tam giác).
Xét tứ giác BFDE có:
FD // BE, DE // BF
Suy ra BFDE là hình chữ nhật.
Câu 9:
Cho tam giác MNP có MN = 6 cm, MP = 9 cm. Trên cạnh MN, MP lần lượt lấy các điểm G, I sao cho MG = 3 cm và MI = 4,5 cm. Khi đó GI song song với đoạn thẳng nào?
Xem đáp án
Đáp án đúng là: A
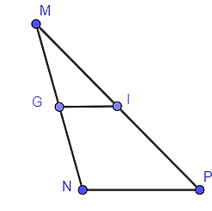
Vì MG = 3 cm, MN = 6 cm, do đó hay G là trung điểm của MN.
MI = 4,5 cm, MP = 9 cm, do đó hay I là trung điểm của MP.
Trong tam giác MNP có G là trung điểm của MN, I là trung điểm của MP.
Do đó GI là đường trung bình của tam giác MNP.
Suy ra GI // NP (tính chất đường trung bình của tam giác).
Câu 10:
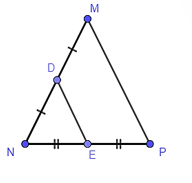
Cho tam giác MNP cân tại M có E và D lần lượt là trung điểm của NP và NM. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: C
Trong tam giác MNP có D là trung điểm MN, E là trung điểm NP.
Do đó DE là đường trung bình của tam giác MNP.
Suy ra DE // MP (tính chất đường trung bình của tam giác).
Suy ra (2 góc đồng vị) (1).
Mà (tam giác MNP cân tại M) hay (2).
Từ (1) và (2) suy ra .
Vậy C đúng.