Trắc nghiệm Toán 7 CTST Bài 9. Tính chất ba đường phân giác của tam giác có đáp án (Phần 2)
Trắc nghiệm Toán 7 CTST Bài 9. Tính chất ba đường phân giác của tam giác có đáp án (Phần 2) (Thông hiểu)
-
271 lượt thi
-
7 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác AOM có \(\widehat A = 52^\circ \). Ba đường phân giác cắt nhau tại I. Số đo góc MIO là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
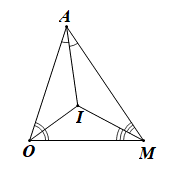
Xét DAOM ba đường phân giác cắt nhau tại I nên OI, MI lần lượt là phân giác của góc AOM, OMA.
Suy ra \(\widehat {IOM} = \widehat {IOA} = \frac{1}{2}\widehat {AOM}\),\(\widehat {IMO} = \widehat {IMA} = \frac{1}{2}\widehat {AMO}\)
Do đó \(\widehat {IMO} + \widehat {IOM} = \frac{1}{2}\left( {\widehat {AMO} + \widehat {AOM}} \right)\)
Xét DMAO có \(\widehat {AMO} + \widehat {AOM} + \widehat {OAM} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {OMA} + \widehat {AOM} = 180^\circ - \widehat {OAM} = 180^\circ - 52^\circ = 128^\circ \).
Do đó \(\widehat {IMO} + \widehat {IOM} = \frac{1}{2}\left( {\widehat {AMO} + \widehat {AOM}} \right) = \frac{1}{2}.128^\circ = 64^\circ \).
Xét DMIO có \(\widehat {IMO} + \widehat {IOM} + \widehat {MIO} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {MIO} = 180^\circ - \left( {\widehat {IMO} + \widehat {IOM}} \right) = 180^\circ - 64^\circ = 116^\circ \).
Vậy ta chọn phương án B.
Câu 2:
Cho tam giác DEG có \(\widehat G = \widehat D + \widehat E\). Hai tia phân giác DA, EB cắt nhau tại H. Số đo góc AHB là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
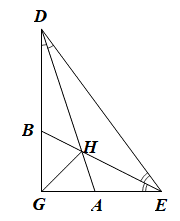
Vì DA là phân giác của góc GDE nên \(\widehat {GDA} = \widehat {E{\rm{D}}A} = \frac{1}{2}\widehat {G{\rm{D}}E}\).
Vì EB là phân giác của góc DEG nên \(\widehat {DEB} = \widehat {{\rm{GEB}}} = \frac{1}{2}\widehat {GED}\).
Do đó \(\widehat {E{\rm{D}}A} + \widehat {DEB} = \frac{1}{2}(\widehat {G{\rm{D}}E} + \widehat {{\rm{GED}}})\)
Xét DDGE có \(\widehat {GE{\rm{D}}} + \widehat {G{\rm{D}}E} + \widehat {EG{\rm{D}}} = 180^\circ \)(tổng ba góc trong một tam giác)
Mà \(\widehat {EG{\rm{D}}} = \widehat {GE{\rm{D}}} + \widehat {G{\rm{D}}E}\) (giả thiết)
Suy ra \(\widehat {EG{\rm{D}}} = \widehat {GE{\rm{D}}} + \widehat {G{\rm{D}}E} = 180^\circ :2 = 90^\circ \)
Do đó \(\widehat {E{\rm{D}}A} + \widehat {DEB} = \frac{1}{2}(\widehat {G{\rm{D}}E} + \widehat {{\rm{GED}}}) = \frac{1}{2}.90^\circ = 45^\circ \).
Xét DDHE có \(\widehat {DHE} + \widehat {DEH} + \widehat {H{\rm{D}}E} = 180^\circ \)(tổng ba góc trong một tam giác)
Suy ra \(\widehat {DHE} = 180^\circ - (\widehat {DEH} + \widehat {H{\rm{D}}E}) = 180^\circ - 45^\circ = 135^\circ \).
Lại có \(\widehat {AHB} = \widehat {DHE}\) (hai góc đối đỉnh)
Do đó \(\widehat {AHB} = 135^\circ \)
Vậy ta chọn phương án A.
Câu 3:
Cho ΔABC cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
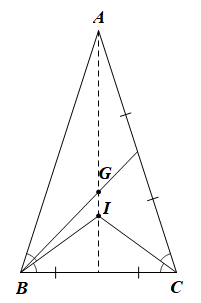
Vì I là giao điểm của các đường phân giác trong tam giác ABC nên I cách đều ba cạnh của ΔABC, do đó phương án A là sai.
Vì G là trọng tâm của tam giác ABC, không phải giao điểm ba đường trung trực nên G không cách đều ba đỉnh của ΔABC, do đó phương án C là sai.
Xét ΔABC cân tại A có AI là đường phân giác của góc BAC nên AI cũng là đường trung tuyến và AI đi qua trọng tâm G của tam giác ΔABC.
Suy ra A, I, G thẳng hàng nên phương án B là đúng.
Vậy ta chọn phương án B.
Câu 4:
Cho tam giác ABC có các tia phân giác cắt nhau tại I. Qua I kẻ đường thẳng song song với BC cắt AB lại E, cắt AC tại F. Biết BE = 1 cm, CF = 2 cm. Độ dài đoạn EF là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
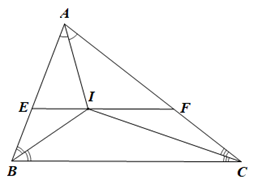
• Vì BI là tia phân giác của góc ABC nên \(\widehat {ABI} = \widehat {CBI}\).
Lại có EI // BC (giả thiết) nên \(\widehat {EIB} = \widehat {CBI}\) (hai góc so le trong)
Do đó \(\widehat {EIB} = \widehat {EBI}\).
Suy ra tam giác BEI cân tại E nên EI = EB = 1 cm.
• Chứng minh tương tự ta cũng có: \(\widehat {FIC} = \widehat {FCI}\)
Do đó tam giác CFI cân tại F nên FI = FC = 2 cm.
Ta có FE = FI + IE = 2 + 1 = 3 (cm)
Vậy ta chọn phương án B.
Câu 5:
Cho tam giác ABC có AH ⊥ BC và \(\widehat {BAH} = 2\widehat {BCA}\). Tia phân giác của góc B cắt AC tại E, tia phân giác của góc BAH cắt BE ở I. Số đo góc BEC là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
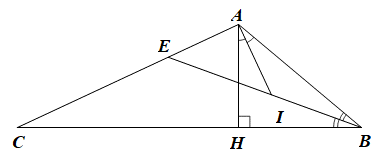
• Vì AI là tia phân giác của \(\widehat {BAH}\) nên \(\widehat {HAI} = \frac{1}{2}\widehat {BAH}\)
Mà \(\widehat {BAH} = 2\widehat {BCA}\) nên \(\widehat {BCA} = \widehat {HAI} = \frac{1}{2}\widehat {BAH}\).
• Vì BE là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {CBE} = \frac{1}{2}\widehat {ABH}\).
• Vì DABH vuông tại H nên \(\widehat {BAH} + \widehat {HBA} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra \(2\left( {\widehat {BCA} + \widehat {CBE}} \right) = 90^\circ \) nên \(\widehat {BCA} + \widehat {CBE} = 90^\circ :2 = 45^\circ \).
• Xét DCBE có \(\widehat {BCE} + \widehat {CBE} + \widehat {BEC} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {BEC} = 180^\circ - \left( {\widehat {BCE} + \widehat {CBE}} \right) = 180^\circ - 45^\circ = 135^\circ .\)
Vậy ta chọn phương án A.
Câu 6:
Cho tam giác DEG có \(\widehat G = \frac{1}{3}\widehat D = \frac{1}{5}\widehat E\). Vẽ các đường phân giác DM, EN. Số đo góc GMD là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
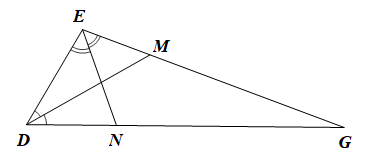
Xét DDEG có \(\widehat {DEG} + \widehat {DGE} + \widehat {E{\rm{DG}}} = 180^\circ \) (tổng ba góc trong một tam giác)
Mà \(\widehat {DGE} = \frac{1}{3}\widehat {EDG} = \frac{1}{5}\widehat {DEG}\) nên \(\widehat {DEG} = 5\widehat {DGE};\widehat {EDG} = 3\widehat {DGE}\)
Suy ra \(5.\widehat {DGE} + \widehat {DGE} + 3.\widehat {DGE} = 180^\circ \)
Hay \(9.\widehat {DGE} = 180^\circ \)
Do đó \(\widehat {DGE} = 180^\circ :9 = 20^\circ \).
Khi đó \(\widehat {EDG} = 3.20^\circ = 60^\circ \).
Vì DM là đường phân giác của góc EDG
Nên \(\widehat {G{\rm{DM}}} = \widehat {MDE} = \frac{1}{2}\widehat {G{\rm{D}}E} = \frac{1}{2}.60^\circ = 30^\circ \).
Xét DDMG có \(\widehat {DMG} + \widehat {DGM} + \widehat {GDM} = 180^\circ \) (tổng ba góc trong một tam giác)
Mà \(\widehat {DGM} = 20^\circ \), \(\widehat {G{\rm{DM}}} = 30^\circ \)
Suy ra \(\widehat {DMG} = 180^\circ - 20^\circ - 30^\circ = 130^\circ \).
Vậy ta chọn phương án C.
Câu 7:
Cho tam giác ABC có các đường phân giác cắt nhau tại I. Biết \(\widehat {BIC} = 126^\circ .\) Khi đó \(\widehat {BAI}\) bằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
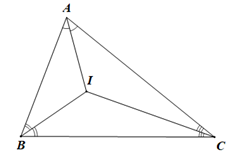
Trong DBIC có \(\widehat {BIC} + \widehat {IBC} + \widehat {ICB} = {180^o}\) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {IBC} + \widehat {ICB} = 180^\circ - \widehat {BIC} = 180^\circ - 126^\circ = 54^\circ \).
Do BI là tia phân giác của góc ABC nên \(\widehat {IBC} = \frac{1}{2}\widehat {ABC}\);
Do CI là tia phân giác của góc ACB nên \(\widehat {ICB} = \frac{1}{2}\widehat {ACB}\).
Do đó \(\widehat {IBC} + \widehat {ICB} = \frac{1}{2}\widehat {ABC} + \frac{1}{2}\widehat {ACB} = \frac{1}{2}\left( {\widehat {ABC} + \widehat {ACB}} \right)\).
Suy ra \(\widehat {ABC} + \widehat {ACB} = 2.\left( {\widehat {IBC} + \widehat {ICB}} \right) = 2.54^\circ = 108^\circ \).
Trong DABC có \(\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {BAC} = 180^\circ - \left( {\widehat {ABC} + \widehat {ACB}} \right) = 180^\circ - 108^\circ = 72^\circ \).
Do AI là tia phân giác của góc BAC nên \(\widehat {BAI} = \frac{1}{2}\widehat {BAC} = \frac{1}{2}.72^\circ = 36^\circ .\)
Vậy ta chọn phương án B.
