Câu hỏi:
01/02/2024 69Cho tam giác ABC có các tia phân giác cắt nhau tại I. Qua I kẻ đường thẳng song song với BC cắt AB lại E, cắt AC tại F. Biết BE = 1 cm, CF = 2 cm. Độ dài đoạn EF là:
A. 4 cm;
B. 3 cm;
C. 2 cm;
D. 1 cm.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
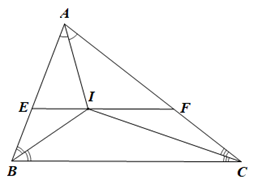
• Vì BI là tia phân giác của góc ABC nên \(\widehat {ABI} = \widehat {CBI}\).
Lại có EI // BC (giả thiết) nên \(\widehat {EIB} = \widehat {CBI}\) (hai góc so le trong)
Do đó \(\widehat {EIB} = \widehat {EBI}\).
Suy ra tam giác BEI cân tại E nên EI = EB = 1 cm.
• Chứng minh tương tự ta cũng có: \(\widehat {FIC} = \widehat {FCI}\)
Do đó tam giác CFI cân tại F nên FI = FC = 2 cm.
Ta có FE = FI + IE = 2 + 1 = 3 (cm)
Vậy ta chọn phương án B.
Hướng dẫn giải
Đáp án đúng là: B

• Vì BI là tia phân giác của góc ABC nên \(\widehat {ABI} = \widehat {CBI}\).
Lại có EI // BC (giả thiết) nên \(\widehat {EIB} = \widehat {CBI}\) (hai góc so le trong)
Do đó \(\widehat {EIB} = \widehat {EBI}\).
Suy ra tam giác BEI cân tại E nên EI = EB = 1 cm.
• Chứng minh tương tự ta cũng có: \(\widehat {FIC} = \widehat {FCI}\)
Do đó tam giác CFI cân tại F nên FI = FC = 2 cm.
Ta có FE = FI + IE = 2 + 1 = 3 (cm)
Vậy ta chọn phương án B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC có các đường phân giác cắt nhau tại I. Biết \(\widehat {BIC} = 126^\circ .\) Khi đó \(\widehat {BAI}\) bằng:
Câu 2:
Cho tam giác AOM có \(\widehat A = 52^\circ \). Ba đường phân giác cắt nhau tại I. Số đo góc MIO là:
Câu 3:
Cho tam giác DEG có \(\widehat G = \widehat D + \widehat E\). Hai tia phân giác DA, EB cắt nhau tại H. Số đo góc AHB là:
Câu 4:
Cho ΔABC cân tại A. Gọi G là trọng tâm của tam giác, I là giao điểm của các đường phân giác trong tam giác. Khẳng định nào đúng?
Câu 5:
Cho tam giác ABC có AH ⊥ BC và \(\widehat {BAH} = 2\widehat {BCA}\). Tia phân giác của góc B cắt AC tại E, tia phân giác của góc BAH cắt BE ở I. Số đo góc BEC là
Câu 6:
Cho tam giác DEG có \(\widehat G = \frac{1}{3}\widehat D = \frac{1}{5}\widehat E\). Vẽ các đường phân giác DM, EN. Số đo góc GMD là:


