Trắc nghiệm Toán 7 Bài tập cuối chương 2 có đáp án
Trắc nghiệm Toán 7 Bài tập cuối chương 2 có đáp án
-
128 lượt thi
-
29 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Số nào sau đây là số thập phân vô hạn tuần hoàn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
115=2,2
2715=3×93×5=95=1,8
129=3×43×3=43=1,(3)
2114=7×37×2=32=1,5
Câu 2:
Cạnh của mặt bàn bằng bao nhiêu, biết mặt bàn hình vuông có diện tích bằng 250 dm2?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Gọi một cạnh của mặt bàn là a
Diện tích của mặt bàn hình vuông là 250 dm2, nên ta có:
a2 = 250
a=√250=15,81138...≈15,81(dm)
Vậy cạnh của mặt bàn hình vuông là 15,81 dm
Câu 3:
Cho tập hợp A viết tập hợp B là tập con của A chỉ chứa các số hữu tỉ?
A = {4,2; 2,(531);√10; 213; −√94}
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Số hữu tỉ là số viết dưới dạng phân số abvới a,b∈Z,b≠0. Gồm các số thập phân hữu hạn và các số thập phân vô hạn tuần hoàn.
Ta có các số:
4,2 là số thập phân hữu hạn.
2,(531) là số thập phân vô hạn tuần hoàn.
√10=3,162277... là số thập phân vô hạn không tuần hoàn.
213=2+13=73=2,(3)là số thập phân vô hạn tuần hoàn.
−√94=−√(32)2=−32=−1,5 là số thập phân hữu hạn.
Câu 4:
Làm tròn số thập phân 3,4256…với độ chính xác là 0,005?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Độ chính xác 0,005 là làm tròn đến phần trăm
Ta gạch chân dưới chữ số hàng phần trăm 3,4256…Nhận thấy chữ số hàng phần nghìn là 5 ≥ 5 nên ta cộng thêm 1 vào chữ số hàng phần trăm và bỏ đi các chữ số thập phân sau hàng phần trăm.
3,4256…≈3,43
Câu 5:
Sử dụng máy tính cầm tay tính 4√27và làm tròn đến chữ số thập phân thứ ba?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Làm tròn đến chữ số thập phân thứ ba là làm tròn đến phần nghìn.
4√27=4√33=12√3=20,7846...
Ta gạch chân dưới chữ số hàng phần nghìn 20,2846…Nhận thấy chữ số hàng phần chục nghìn là 6≥5 nên ta giữ nguyên chữ số hàng phần nghìn và bỏ đi các chữ số thập phân sau hàng phần nghìn.
20,2846…≈20,785
Câu 6:
Xác định tất cả giá trị của x để |x2|=25?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
|x2|=25
x2=52=(−5)2
x = 5 hoặc x = -5
Câu 7:
Nhìn thật nhanh xem đâu là số thập phân hữu hạn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Người ta đã chứng minh được rằng:
-Nếu một phân số tối giản với mẫu dương mà mẫu không có ước nguyên tố khác 2 và 5 thi phân số đỏ vết được dưới dạng số thập phân hữu hạn.
-Nếu một phân số tối giản với mẫu dương mà mẫu có ước nguyên tố khác 2 và 5 thì phân số đó viết được dưới dạng số thập phân vô hạn tuần hoàn.
113 có mẫu số là 3 và mẫu số có ước nguyên tố khác 2 và 5 nên phân số 113 được viết dưới dạng số thập phân vô hạn tuần hoàn.
1511 có mẫu số là 11 và mẫu số có ước nguyên tố khác 2 và 5 nên phân số 1511 được viết dưới dạng số thập phân vô hạn tuần hoàn.
59=532 có mẫu số là 9 và mẫu số có ước nguyên tố khác 2 và 5 nên phân số 59 được viết dưới dạng số thập phân vô hạn tuần hoàn.
235 có mẫu số là 5 và mẫu số là ước của nguyên tố 5 nên phân số 235 được viết dưới dạng số thập phân vô hạn tuần hoàn.
Câu 8:
Số nào dưới đây bằng 32?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: 322 = 1024
\(\sqrt {1024} = \sqrt {{{32}^2}} = 32\)
Câu 9:
Cho một sợi dây dài 23 cm người ta muốn cắt ra thành những sợi dây ngắn hơn dài 3cm, hỏi sau khi cắt cắt được bao nhiêu sợi dây và sợi dây thừa ra dài khoảng bao nhiêu cm
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: 23 = 7.3 + 2
Vậy người này cắt được 7 sợi dây dài 3cm và đoạn còn thừa là 2 cm
Câu 10:
Đâu không phải là số thập phân vô hạn tuần hoàn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
4,474141…= 4,47(41) số thập phân vô hạn tuần hoàn.
3,2101201020… có phần thập phân không tuần hoàn nên 3,2101201020… không phải số thập phân vô hạn tuần hoàn.
0,1233333…= 0,12(3) số thập phân vô hạn tuần hoàn.
7,32454545…= 7,32(45) số thập phân vô hạn tuần hoàn.
Câu 11:
Cho các dãy số sau cho biết căn bậc hai của chúng lần lượt là những số nào?
144; 25; 100; 81; 49
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
√144=12
√25=5
√81=9
√49=7
Câu 12:
Có bao nhiêu phần tử của tập hợp A={x|x∈Z,81≤|x2|≤144}??
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
81≤|x2|≤144
92≤|x2|≤122 hoặc (−9)2≤|x2|≤(−12)2
Nếu x≥0thì x = { 9; 10; 11; 12 }
Nếu x≤0thì x = { -9; -10; -11; -12 }
A ={ -9; -10; -11; -12; 9; 10; 11; 12 } có 8 phần tử.
Câu 13:
Khi viết phân số 139 dưới dạng số thập phân và Làm tròn đến chữ số thập phân thứ ba thì ta được số thập phân khi làm tròn là gì ?
 Xem đáp án
Xem đáp án
Đáp án đúng là:
Làm tròn đến chữ số thập phân thứ ba là làm tròn đến phần nghìn.
139=1,44444...
Ta gạch chân dưới chữ số hàng phần nghìn 1,44444…Nhận thấy chữ số hàng phần vạn là 4 < 5 nên ta giữ nguyên chữ số hàng phần nghìn và bỏ đi các chữ số thập phân sau hàng phần nghìn.
1,44444…≈1,444
Câu 14:
Tính √176400?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
176400=24×32×52×72=(22×3×5×7)2=4202
√176400=√4202=420
Câu 15:
Cho hình dưới đây, hãy cho biết điểm A chỉ số thực nào? Biết điểm A màu đỏ chia 1 ô vuông nhỏ thành 3 phần bằng nhau.
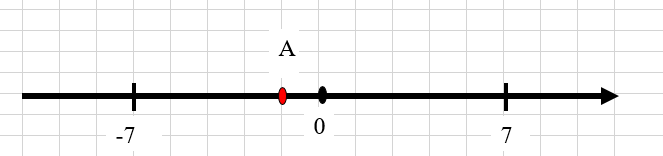
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Từ điểm 0 đến điểm 7 có 5 ô vuông nên 1 ô vuông có độ dài là 75
Điểm A nằm ở cách 0 là 1 ô và nằm ở phía bên trái 0 nên điểm A chỉ số thực là−75 = -1,4.
Câu 16:
Xác định tất cả giá trị của x để |x2|=49?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
|x2|=49
x2 = 49
x2 = 72 = (-7)2
x = 7 hoặc x = -7
Câu 17:
Xác định tất cả giá trị của x để|x|=√25?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
|x|=√25
|x|=√52
|x|=5
x = 5 hoặc x = -5
Câu 18:
Cho tập hợp A viết tập hợp B là tập con của A chỉ chứa các số hữu tỉ?
A={3,4;1,(231);357;6,74283…;−√25}
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Số hữu tỉ là số viết dưới dạng phân số abvới a,b∈Z,b≠0. Gồm các số thập phân hữu hạn và các số thập phân vô hạn tuần hoàn.
3,4 là số thập phân hữu hạn.
1,(231) là số thập phân vô hạn tuần hoàn.
6,74283… có phần tập phân không tuần hoàn nên 6,74283… là số thập phân vô hạn không tuần hoàn
−√25=−√52=−5=−5,0 số thập phân hữu hạn.
357=3+57=267=3,(713285) là số thập phân vô hạn tuần hoàn
Câu 19:
Cho tập hợp A viết tập hợp C là tập con của A chỉ chứa các số vô tỉ?
A ={3,22143…;1,4(21);357;43;−√8}
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Số vô tỉ là các số có dạng số thập phân vô hạn không tuần hoàn.
3,22143… có phần thập phân không tuần hoàn nên 3,22143… là số thập phân vô hạn không tuần hoàn.
1,4(21) là số thập phân vô hạn tuần hoàn.
357=3+57=267=3,(713285) là số thập phân vô hạn tuần hoàn.
43 = 1,(3) là số thập phân vô hạn tuần hoàn.
−√8=−2,828427... có phần thập phân không tuần hoàn nên -2,828427… là số thập phân vô hạn không tuần hoàn.
Câu 20:
Khi viết hỗn số 253 dưới dạng số thập phân thì ta được kết quả khi viết gọn số thập phân đó là gì ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
253=2+53=2×3+53=113=3,6666...=3,(6) là số thập phân vô hạn tuần hoàn.
Câu 21:
Làm tròn số thập phân 0,354536… đến chữ số thập phân thứ ba?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Làm tròn số thập phân đến chữ số thập phân thứ ba là làm tròn đến phần nghìn.
Ta gạch chân dưới chữ số hàng phần nghìn 0,354536… Nhận thấy chữ số hàng phần mười nghìn là 5 ≥ 5 nên ta cộng thêm 1 vào chữ số hàng phần nghìn và bỏ đi các chữ số thập phân sau hàng phần trăm.
0,354536… ≈0,355
Câu 22:
Làm tròn số 435678,21 với độ chính xác là 50?
 Xem đáp án
Xem đáp án
Đáp án đúng là:
Làm tròn số độ chính xác là 50 là làm tròn đến hàng trăm.
Ta gạch chân dưới chữ số hàng trăm 435678,21. Nhận thấy chữ số hàng chục là 7≥5 nên ta cộng thêm 1 vào chữ số hàng phần trăm và bỏ đi các chữ số sau hàng trăm.
435678,21≈435700
Câu 23:
Đâu là số thập phân vô hạn tuần hoàn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
3,243564… có phần thập phân không tuần hoàn nên 3,243564… không phải số thập phân vô hạn tuần hoàn.
3,101001000… có phần thập phân không tuần hoàn nên 3,101001000… không phải số thập phân vô hạn tuần hoàn.
5,31241212… = 5,3124(12) là số thập phân vô hạn tuần hoàn.
7,2132123… có phần thập phân không tuần hoàn nên 7,2132123… không phải số thập phân vô hạn tuần hoàn.
Câu 24:
Một người muốn làm một con diều hình vuông có diện tích là 4900 cm2 . Hỏi người đó cần một mảnh giấy hình vuông có 1 cạnh bằng bao nhiêu? (Coi các mép không đáng kể)
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Gọi cạnh của con diều là: a
Diện tích con diều là S = a2 = 4900. Do đó:
a=√4900=√702=70cm
Đổi: 70 cm =7 dm
Vậy một cạnh của con diều có độ dài là 7 dm
Câu 25:
Hãy viết gọn số thập phân vô hạn tuần hoàn 3,2121212…?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
3,2121212…=3,(21)
Câu 26:
Cạnh của bàn cờ vua bằng bao nhiêu, biết bàn cơ vua hình vuông có diện tích bằng 400 cm2?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi cạnh của bàn cờ là a
Ta có: Diện tích bàn cờ = a2 = 400
Nên ta được a=√400=√202=20
Vậy cạnh của bàn cờ là 20 cm.
Câu 27:
Sử dụng máy tính cầm tay tính √94và làm tròn đến chữ số thập phân thứ hai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Làm tròn đến chữ số thập phân thứ hai là làm tròn đến phần trăm.
Ta có: √94=9,69535...
Ta gạch chân dưới chữ số hàng phần trăm 9,69535…Nhận thấy chữ số hàng phần nghìn là 5 ≥ 5 nên ta cộng thêm 1 vào chữ số hàng phần trăm và bỏ đi các chữ số thập phân sau hàng phần trăm. Vì 9 + 1 = 10 nên ta cộng thêm 1 vào chữ số phần chục.
√94≈9,7
Câu 28:
Hãy so sánh |−145| và |95|?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
|−145|=|−(1+45)|=|−95|=95
|95|=95
Mà 95=95nên |−145| = |95|
