10 câu hỏi trắc nghiệm thuộc Dạng 4. Bài toán thực tiễn liên quan đến hàm số lượng giác

Câu 1:

Hằng ngày, mực nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh được tính tại thời điểm t (giờ) trong một ngày bởi công thức $h (t) = 3 \cos (\frac{π t}{8} + \frac{π}{4}) + 12$ . Mực nước của con kênh cao nhất khi

A. t = 13 (giờ);

B. t = 14 (giờ);

C. t = 15 (giờ);

D. t = 16 (giờ).

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Mực nước của con kênh cao nhất khi h đạt giá trị lớn nhất

$\Leftrightarrow \cos (\frac{π t}{8} + \frac{π}{4}) = 1 \Leftrightarrow \frac{π t}{8} + \frac{π}{4} = k 2 π (k \in ℤ) \Leftrightarrow t = 16 k - 2 (k \in ℤ)$ (1).

Mặt khác 0 ≤ t ≤ 24, kết hợp với (1) ta được: $\frac{1}{8} \leq k \leq \frac{13}{8}, k \in ℤ$ . Do đó k = 1.

Với k = 1 thì t = 14 (giờ).

Vậy mực nước của con kênh cao nhất khi t = 14 giờ.

Câu 2:

Một cây cầu có dạng cung OA là một phần của đồ thị hàm số $y = 4, 8 \sin \frac{x}{9}$ và được mô tả trong hệ trục tọa độ với đơn vị trục là mét như hình dưới.

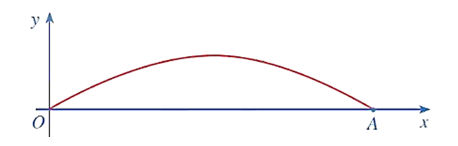
Một cây cầu có dạng cung OA là một phần của đồ thị hàm số y= 4,8 sin x/9 và được mô tả trong hệ trục (ảnh 1)

Giả sử chiều rộng của con sông là độ dài đoạn thẳng OA. Chiều rộng đó (làm tròn đến kết quả hàng phần mười) là

A. 28,3 m;

B. 14,1 m;

C. 18,3 m;

D. 24,1 m.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Hai vị trí O và A là hai vị trí chân cầu, tại hai vị trí này thì y = 0.

Ta có y = 0 $\Leftrightarrow 4, 8 \sin \frac{x}{9} = 0 \Leftrightarrow \sin \frac{x}{9} = 0 \Leftrightarrow \frac{x}{9} = k π$ (k ∈ ℤ).

Suy ra x = 9kπ, k ∈ ℤ.

Quan sát đồ thị ta thấy, đồ thị hàm số $y = 4, 8 \sin \frac{x}{9}$ cắt trục hoành tại điểm O và A liên tiếp nhau với x ≥ 0.

Xét k = 0, ta có x₁ = 0;

Xét k = 1, ta có x₂ = 9π.

Mà x₁ = 0 nên đây là hoành độ của O, do đó x₂ = 9π là hoành độ của điểm A.

Khi đó OA = 9π ≈ 28,3.

Vậy chiều rộng của con sông xấp xỉ 28,3 m.

Câu 3:

Trong Địa lí, phép chiếu hình trụ được sử dụng để vẽ một bản đồ phẳng như trong hình vẽ. Trên bản đồ phẳng lấy đường xích đạo làm trục hoành và kinh tuyến 0° làm trục tung. Khi đó tung độ của một điểm có vĩ độ φ° (–90 < φ < 90) được cho bởi hàm số $y = 20 \tan (\frac{π}{180} φ)$ (cm). Sử dụng đồ thị hàm số tan, hãy cho biết những điểm ở vĩ độ nào nằm cách xích đạo không quá 20 cm trên bản đồ.

Trong Địa lí, phép chiếu hình trụ được sử dụng để vẽ một bản đồ phẳng như trong hình vẽ (ảnh 1)

A. Vĩ độ từ –120° đến 120°;

B. Vĩ độ từ –75° đến 75°;

C. Vĩ độ từ –45° đến 45°;

D. Vĩ độ từ –90° đến 90°.

Xem đáp án

Trong Địa lí, phép chiếu hình trụ được sử dụng để vẽ một bản đồ phẳng như trong hình vẽ (ảnh 2)

Câu 4:

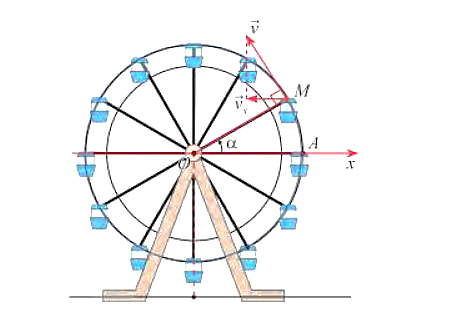
Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác α = (Ox, OM) theo hàm số v_x = 0,3sinα (m/s) (hình vẽ). Dựa vào đồ thị của hàm số sin, hãy cho biết trong vòng quay đầu tiên (0 ≤ α ≤ 2π), góc α ở trong khoảng nào sau đây thì v_x giảm?

Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác (ảnh 1)

A. $(\frac{π}{2}; 2 π)$ ;

B. $(\frac{3 π}{2}; 2 π)$ ;

C. $(0; \frac{π}{2})$ ;

D.

(\frac{π}{2}; π)

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Ta có đồ thị hàm số v_x = 0,3sinα

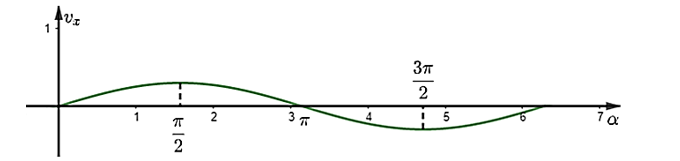
Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin M phụ thuộc vào góc lượng giác (ảnh 2)

Theo đồ thị, với góc $α \in (\frac{π}{2}; π)$ hoặc $α \in (π; \frac{3 π}{2})$ thì v_x giảm (đồ thị hàm số đi xuống từ trái qua phải).

Câu 5:

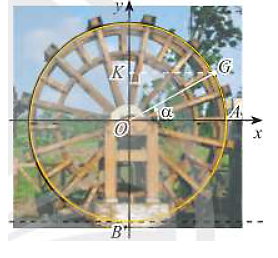
Khoảng cách từ tâm một guồng nước đến mặt nước và bán kính của guồng đều bằng 3 m. Xét gàu G của guồng. Ban đầu gàu G nằm ở vị trí A (hình vẽ). Viết hàm số h biểu diễn chiều cao (tính bằng mét) của gàu G so với mặt nước theo góc α = (OA, OG).

Khoảng cách từ tâm một guồng nước đến mặt nước và bán kính của guồng đều bằng 3 m. (ảnh 1)

A. h = 3sinα;

B. h = 3 + 3sinα;

C. h = 1 + 3sinα;

D. h = 2 + 3sinα.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Điểm G là điểm biểu diễn cho góc lượng giác có số đo α. Bán kính của guồng là 3 m.

Khi đó tọa độ điểm G là (3cosα; 3sinα).

Do OB = 3 m nên chiều cao của gàu đến mặt nước là: h = 3 + 3sinα.

Câu 6:

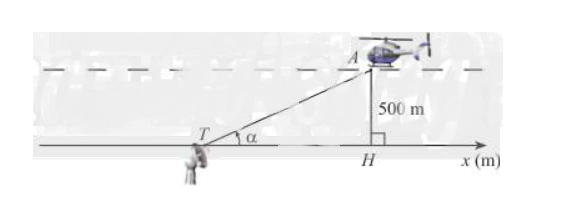
Trong hình vẽ, một chiếc máy bay A bay ở độ cao 500 m theo một đường thẳng đi ngang qua phía trên trạm quan sát T ở mặt đất. Hình chiếu vuông góc của A lên mặt đất là H, α là góc lượng giác (Tx, TA) (0 < α < π). Biểu diễn tọa độ x_H của điểm H lên trục Tx theo α.

Trong hình vẽ, một chiếc máy bay A bay ở độ cao 500 m theo một đường thẳng đi ngang qua (ảnh 1)

A. x_H= 500cotα;

B. x_H= 500cosα;

C. x_H= 500sinα;

D. x_H= 500tanα.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Xét tam giác AHT vuông tại H có:

$\cot α = \frac{T H}{A H} \Leftrightarrow T H = A H \cdot \cot α = 500 \cdot \cot α$

Vậy trên trục Tx, tọa độ x_H= 500cotα.

Câu 7:

Huyết áp là áp lực máu cần thiết tác động lên thành động mạch nhằm đưa máu đi nuôi dưỡng các mô trong cơ thể. Nhờ lực co bóp của tim và sức cản của động mạch mà huyết áp được tạo ra. Huyết áp tối đa và huyết áp tối thiểu được gọi tương ứng là huyết áp tâm thu và huyết áp tâm trương. Chỉ số huyết áp của chúng ta được tính bằng huyết áp tâm thu/huyết áp tâm trương. Tính chỉ số huyết áp. Giả sử huyết áp của người đó thay đổi theo thời gian được cho bởi công thức:

p(t) = 115 + 25sin160πt,

trong đó p(t) là huyết áp tính theo đơn vị mmHg (milimet thủy ngân) và thời gian t tính theo đơn vị phút.

A. 100/90;

B. 150/60;

C. 120/80;

D. 140/90.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Ta có –1 ≤ sin160πt ≤ 1 ⇔ –25 ≤ 25sin160πt ≤ 25 ⇔ 90 ≤ 115 + 25sin160πt ≤ 140 ∀t.

Vậy huyết áp tâm thu của người đó là 140, huyết áp tâm trương là 90.

Do đó chỉ số huyết áp là 140/90.

Câu 8:

Hằng ngày, Mặt Trời chiếu sáng, bóng của một toà chung cư cao 40 m in trên mặt đất, độ dài bóng của toà nhà này được tính bằng công thức $S (t) = 40 |\cot \frac{π}{12} t|$ , ở đó S được tính bằng mét, còn t là số giờ tính từ 6 giờ sáng. Tại những thời điểm nào thì độ dài bóng của tòa nhà bằng chiều cao tòa nhà?

A. 9 giờ sáng và 15 giờ chiều;

B. 3 giờ sáng và 9 giờ sáng;

C. 12 giờ trưa và 15 giờ chiều;

D. 9 giờ sáng và 12 giờ trưa.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Độ dài bóng của tòa nhà bằng chiều cao của tòa nhà khi: S(t) = 40

$\Leftrightarrow 40 |\cot \frac{π}{12} t| = 40 \Leftrightarrow \cot \frac{π}{12} t = \pm 1$ .

Do đó: $\frac{π}{12} t = \pm \frac{π}{4} + k π, k \in ℤ$ .

Suy ra: t = ±3 + 12k, k ∈ ℤ.

Vì 0 ≤ t ≤ 12. Do đó, t = 3 hoặc t = 9.

Vì t là số giờ tính từ 6 giờ sáng, do vậy tại thời điểm 9 giờ sáng (6 + 3 = 9) và 15 giờ chiều (6 + 9 = 15) thì bóng của tòa nhà dài bằng chiều cao của tòa nhà.

Câu 9:

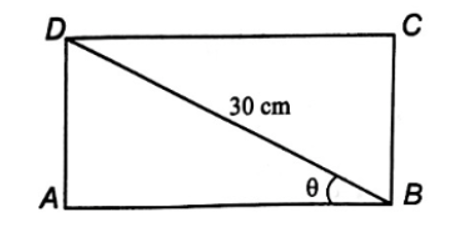
Một thanh xà gồ hình chữ nhật được cắt ra từ một khối gỗ hình trụ có đường kính 30 cm. Hãy tìm sự phụ thuộc giữa diện tích mặt cắt S của thanh xà gồ với góc θ, trong đó góc θ được chỉ ra ở hình dưới.

Một thanh xà gồ hình chữ nhật được cắt ra từ một khối gỗ hình trụ có đường kính 30 cm. Hãy tìm (ảnh 1)

A. S(θ) = 450sin2θ (cm²);

B. S(θ) = 900sin2θ (cm²);

C. S(θ) = 225sin2θ (cm²);

D. S(θ) = 1800sin2θ (cm²).

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Một thanh xà gồ hình chữ nhật được cắt ra từ một khối gỗ hình trụ có đường kính 30 cm. Hãy tìm (ảnh 2)

Mặt cắt của thanh xà gồ là hình chữ nhật có hai kích thước là

AB = 30cos θ (cm) và AD = 30sin θ (cm).

Vậy diện tích mặt cắt là

S = AB ∙ AD = 30cosθ ∙ 30sinθ = 450 ∙ 2sinθ cosθ = 450sin2θ (cm²).

Câu 10:

Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức $h (t) = 29 + 3 \sin \frac{π}{12} (t - 9)$ , với h được tính bằng độ C và t là thời gian trong ngày tính bằng giờ. Nhiệt độ thấp nhất trong ngày là

A. 27℃;

B. 32℃;

C. 26℃;

D. 30℃.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Vì $- 1 \leq \sin \frac{π}{12} (t - 9) \leq 1$ nên $26 \leq 29 + 3 \sin \frac{π}{12} (t - 9) \leq 32$ .

Do đó nhiệt độ thấp nhất trong ngày là 26℃.

Trắc nghiệm Toán 11 Bài 3. Hàm số lượng giác có đáp án

Dạng 4. Bài toán thực tiễn liên quan đến hàm số lượng giác

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương