10 câu hỏi trắc nghiệm thuộc Dạng 2: Nhận biết và chứng minh hai mặt phẳng vuông góc có đáp án

Câu 1:

Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?

A. Góc giữa hai mặt phẳng (ABC) và (ABD) là

\hat{C B D}

;

B. Góc giữa hai mặt phẳng (ACD) và (BCD) là

\hat{A I B}

;

C. (BCD) ^ (AIB);

D. (ACD) ^ (AIB).

Xem đáp án

Đáp án đúng là: A

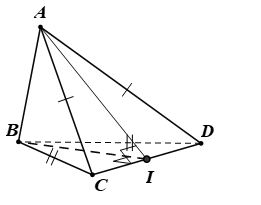
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai? (ảnh 1)

Tam giác BCD cân tại B có I là trung điểm đáy CD ⇒ CD ^ BI (1).

Tam giác ACD cân tại A có I là trung điểm đáy CD ⇒ CD ^ AI (2).

Do đó góc giữa hai mặt phẳng (ACD) và (BCD) là . Suy ra đáp án B đúng.

(1) và (2) ⇒ CD ^ (ABI).

Mà CD Ì (BCD) ⇒ (BCD) ^ (ABI). Suy ra đáp án C đúng.

CD Ì (ACD) ⇒ (ACD) ^ (ABI). Suy ra đáp án D đúng.

Câu 2:

Cho hình chóp S.ABC có SA ^ (ABC) và đáy ABC vuông ở A. Khẳng định nào sau đây sai?

A. (SAB) ^ (ABC);

B. (SAB) ^ (SAC);

C. Vẽ AH ^ BC, H Î BC ⇒

\hat{A H S}

là góc giữa hai mặt phẳng (SBC) và (ABC);

D. Góc giữa hai mặt phẳng (SBC) và (SAC) là góc

\hat{S C B}

.

Xem đáp án

Đáp án đúng là: D

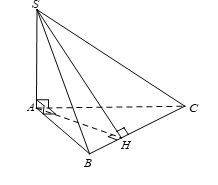
Cho hình chóp S.ABC có SA ^ (ABC) và đáy ABC vuông ở A. Khẳng định nào sau đây sai? (ảnh 1)

Vì SA ^ (ABC) mà SA Ì (SAB) ⇒ (SAB) ^ (ABC). Do đó đáp án A đúng.

Vì SA ^ (ABC) nên SA ^ AB mà AB ^ AC suy ra AB ^ (SAC).

Lại có AB Ì (SAB) nên (SAB) ^ (SAC). Do đó đáp án B đúng.

Có AH ^ BC và BC ^ SA (do SA ^ (ABC)) do đó BC ^ (SAH) ⇒ BC ^ SH.

Do đó góc giữa hai mặt phẳng (SBC) và (ABC) bằng $\hat{S H A}$ . Do đó đáp án C đúng.

Vậy đáp án D sai.

Câu 3:

Cho tứ diện ABCD có AB ^ (BCD). Trong DBCD vẽ các đường cao BE và DF. Trong (ADC) vẽ DK ^ AC tại K. Khẳng định nào sau đây sai?

A. (ADC) ^ (ABE);

B. (ADC) ^ (DFK);

C. (ADC) ^ (ABC);

D. (BDC) ^ (ABE).

Xem đáp án

Đáp án đúng là: C

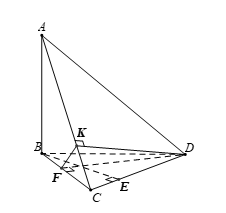
Cho tứ diện ABCD có AB ^ (BCD). Trong DBCD vẽ các đường cao BE và DF. Trong (ADC) vẽ DK ^ AC tại K. Khẳng định nào sau đây sai? (ảnh 1)

Vì AB ^ (BCD) nên AB ^ CD mà BE ^ CD suy ra CD ^ (ABE).

Lại có CD Ì (ADC) nên (ADC) ^ (ABE). Do đó đáp án A đúng.

Vì AB ^ (BCD) nên AB ^ DF mà DF ^ BC suy ra DF ^ (ABC) ⇒ DF ^ AC.

Lại có DK ^ AC nên AC ^ (DFK).

Mặt khác AC Ì (ADC) suy ra (ADC) ^ (DFK). Do đó đáp án B đúng.

Vì CD ^ (ABE) mà CD Ì (BCD) suy ra (BDC) ^ (ABE). Do đó đáp án D đúng.

Vậy đáp án C sai.

Câu 4:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi và SB vuông góc với mặt phẳng (ABCD). Mặt phẳng nào sau đây vuông góc với mặt phẳng (SBD)?

A. (SBC);

B. (SAD);

C. (SCD);

D. (SAC).

Xem đáp án

Đáp án đúng là: D

Cho hình chóp S.ABCD có đáy ABCD là hình thoi và SB vuông góc với mặt phẳng (ABCD). Mặt phẳng nào sau đây vuông góc với mặt phẳng (SBD)? (ảnh 1)

Vì ABCD là hình thoi nên AC ^ BD.

Do SB ^ (ABCD) ⇒ SB ^ AC mà AC ^ BD nên AC ^ (SBD).

Lại có AC Ì (SAC) ⇒ (SAC) ^ (SBD).

Câu 5:

Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, cạnh bên SA vuông góc với đáy, I là trung điểm AC, H là hình chiếu của I lên SC. Khẳng định nào sau đây đúng?

A. (BIH) ^ (SBC);

B. (SAC) ^ (SAB);

C. (SBC) ^ (ABC);

D. (SAC) ^ (SBC).

Xem đáp án

Đáp án đúng là: A

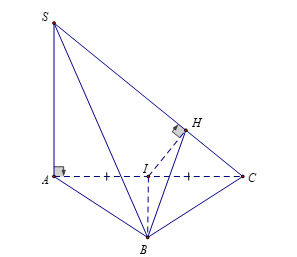
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, cạnh bên SA vuông góc với đáy, I là trung điểm AC, (ảnh 1)

Vì DABC cân tại B, BI là đường trung tuyến nên BI đồng thời là đường cao.

Suy ra BI ^ AC.

Mà SA ^ (ABC) ⇒ SA ^ BI mà BI ^ AC nên BI ^ (SAC) ⇒ BI ^ SC (1).

Lại có IH ^ SC (2).

Từ (1) và (2, suy ra SC ^ (BIH) mà SC Ì (SBC). Do đó (BIH) ^ (SBC).

Câu 6:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA ^ (ABC), gọi M là trung điểm của AC. Mệnh đề nào sai ?

A. (SAB) ^ (SAC);

B. BM ^ AC;

C. (SBM) ^ (SAC);

D. (SAB) ^ (SBC).

Xem đáp án

Đáp án đúng là: A

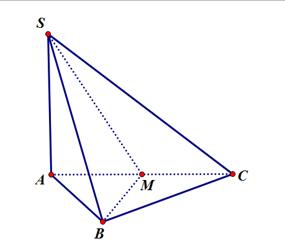
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA ^ (ABC), gọi M là trung điểm của AC. (ảnh 1)

+) Vì BM là trung tuyến của tam giác vuông cân ABC nên BM ^ AC.

+) Vì SA ^ (ABC) nên SA ^ BM mà BM ^ AC nên BM ^ (SAC) ⇒ (SBM) ^ (SAC).

+) Vì SA ^ (ABC) nên SA ^ BC mà AB ^ BC (do DABC vuông cân) nên BC ^ (SAB).

Mà BC Ì (SBC) ⇒ (SBC) ^ (SAB).

Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA = SC. Khẳng định nào sau đây đúng?

A. Mặt phẳng (SBD) vuông góc với mặt phẳng (ABCD);

B. Mặt phẳng (SBC) vuông góc với mặt phẳng (ABCD);

C. Mặt phẳng (SAD) vuông góc với mặt phẳng (ABCD);

D. Mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD).

Xem đáp án

Đáp án đúng là: A

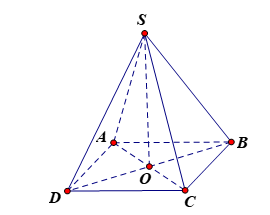
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA = SC. Khẳng định nào sau đây đúng? (ảnh 1)

Gọi O là giao điểm của AC, BD. Suy ra O là trung điểm của AC và BD.

Vì ABCD là hình thoi nên AC ^ BD (1).

Vì SA = SC nên DSAC cân tại S mà SO là trung tuyến nên SO đồng thời là đường cao hay SO ^ AC (2).

Từ (1) và (2), suy ra AC ^ (SBD) mà AC Ì (ABCD) nên (SBD) ^ (ABCD).

Câu 8:

Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a; CD = 2x. Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc?

A. $\frac{a \sqrt{3}}{3}$

B. $\frac{a}{2}$

C. $\frac{a \sqrt{2}}{2}$

D. $\frac{a}{3}$

Xem đáp án

Đáp án đúng là: A

Câu 9:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Trong số các mặt phẳng chứa mặt đáy và các mặt bên của hình chóp, có bao nhiêu mặt phẳng vuông góc với mặt phẳng (SAB)?

A. 4;

B. 3;

C. 1;

D. 2.

Xem đáp án

Đáp án đúng là: B

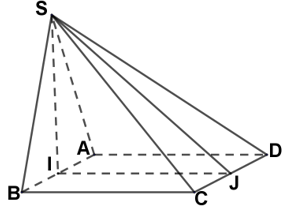
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc (ảnh 1)

Gọi I, J lần lượt là trung điểm AB và CD.

Do DSAB đều nên SI ^ AB (1).

Lại có (SAB) ^ (ABCD) mà (SAB) Ç (ABCD) = AB nên SI ^ (ABCD) ⇒ SI ^ BC.

Lại có BC ^ AB mà SI ^ BC ⇒ BC ^ (SAB) mà BC Ì (SBC) ⇒ (SBC) ^ (SAB).

Tương tự, (SAD) ^ (SAB).

Vì AB // CD mà SI ^ AB nên SI ^ CD.

Lại có IJ ^ CD nên CD ^ (SIJ) ⇒ CD ^ SJ (2).

Vì $\begin{array}{l} S \in (S A B) \cap (S C D) \\ A B / / C D \end{array}\} \Rightarrow (S A B) \cap (S C D) = S x (S x / / A B / / C D)$ (3).

Từ (1), (2), (3), ta có: ((SAB), (SCD)) = (SI, SJ) = $\hat{IS J} \neq 90 °$ .

Câu 10:

Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với đáy (ABC), tam giác (ABC) vuông cân ở A và có đường cao AH. Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây đúng?

A. SC ^ (ABC);

B. (SAH) ^ (SBC);

C. O Î SC;

D. Góc giữa (SBC) và (ABC) là góc

\hat{S B A}

.

Xem đáp án

Đáp án đúng là: B

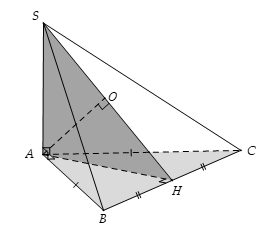
Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với đáy (ABC), tam giác (ABC) vuông cân ở A (ảnh 1)

Ta có: $\{\begin{matrix} (S A B) \cap (S A C) = S A \\ (S A C) ⊥ (A B C) \\ (S A B) ⊥ (A B C) \end{matrix} \Rightarrow S A ⊥ (A B C) \Rightarrow S A ⊥ B C$ .

Gọi H là trung điểm của BC và DABC vuông cân ⇒ AH ^ BC

mà BC ^ SA ⇒ BC ^ (SAH) ⇒ (SBC) ^ (SAH).

Khi đó O là hình chiếu vuông góc của A lên (SBC)

Thì suy ra O Î SH.

Khi đó góc giữa (SBC) và (ABC) là góc $\hat{S H A}$ .

Vậy đáp án B đúng.

Trắc nghiệm Toán 11 Bài 25. Hai mặt phẳng vuông góc có đáp án

Dạng 2: Nhận biết và chứng minh hai mặt phẳng vuông góc có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương