10 câu hỏi trắc nghiệm thuộc Dạng 1: Xác định và tính góc giữa hai mặt phẳng có đáp án

Câu 1:

Cho hình chóp S.ABCD với đáy ABCD là hình vuông có cạnh 2a, $S A = a \sqrt{6}$ và vuông góc với đáy. Góc giữa (SBD) và (ABCD) bằng

A. 90°;

B. 30°;

C. 45°;

D. 60°.

Xem đáp án

Đáp án đúng là: D

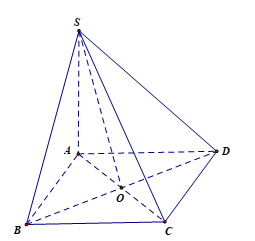
Cho hình chóp S.ABCD với đáy ABCD là hình vuông có cạnh 2a, (ảnh 1)

Gọi O là giao điểm của AC và BD. Suy ra O là trung điểm của AC và BD.

Vì ABCD là hình vuông nên AO ^ BD.

Mà SA ^ (ABCD) nên SA ^ BD.

Lại có AO ^ BD nên BD ^ (SAC) ⇒ BD ^ SO.

Do đó góc giữa (SBD) và (ABCD) bằng $\hat{S O A}$ .

Xét ∆ABC vuông tại B, có $A C = \sqrt{A B^{2} + B C^{2}} = 2 a \sqrt{2}$ .

Mà O là trung điểm AC nên $A O = \frac{A C}{2} = a \sqrt{2}$ .

Xét ∆SAO vuông tại A, $\tan \hat{S O A} = \frac{S A}{A O} = \frac{a \sqrt{6}}{a \sqrt{2}} = \sqrt{3} \Rightarrow \hat{S O A} = 60 °$ .

Câu 2:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, $\hat{A B C} = 60 °$ , tam giác SBC là tam giác đều có cạnh 2a và nằm trong mặt phẳng vuông góc với đáy. Tính tan của góc giữa hai mặt phẳng (SAC) và (ABC).

A. $\sqrt{3}$

B. $2 \sqrt{3}$

C. $\frac{\sqrt{3}}{6}$

D. $\frac{1}{2}$

Xem đáp án

Đáp án đúng là: B

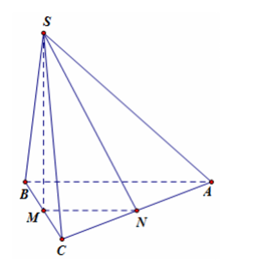
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, góc ABC=60 độ , tam giác SBC là tam giác đều có cạnh 2a (ảnh 1)

Gọi M là trung điểm của BC.

Vì ∆SBC đều nên SM ^ BC, $S M = \frac{2 a \sqrt{3}}{2} = a \sqrt{3}$ .

Ta có (SBC) ^ (ABC) và SM ^ BC ⇒ SM ^ (ABC) ⇒ SM ^ AC.

Gọi N là trung điểm của AC ⇒ MN // AB mà AB ^ AC suy ra MN ^ AC.

Ta có SM ^ AC và MN ^ AC ⇒ AC ^ (SMN) ⇒ AC ^ SN .

Do đó góc giữa hai mặt phẳng (SAC) và (ABC) bằng $\hat{S N M}$ .

Xét ∆ABC vuông tại A, có AB = BC∙cos60° = a.

Vì MN là đường trung bình của ∆ABC nên $M N = \frac{A B}{2} = \frac{a}{2}$ .

Xét ∆SMN vuông tại M, $\tan \hat{S N M} = \frac{S M}{M N} = 2 \sqrt{3}$ .

Câu 3:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và $S O = \frac{a \sqrt{3}}{2}$ . Tính góc giữa hai mặt phẳng (SBC) và (ABCD).

A. 30°;

B. 45°

C. 60°;

D. 90°.

Xem đáp án

Đáp án đúng là: C

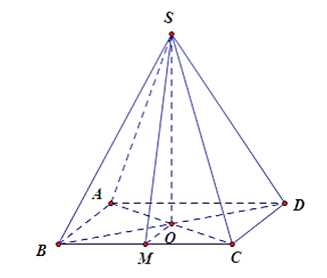
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) (ảnh 1)

Vì SO ^ (ABCD) nên SO ^ BC.

Gọi M là trung điểm của BC ⇒ OM ^ BC.

Vì SO ^ BC và OM ^ BC nên BC ^ (SOM) ⇒ BC ^ SM.

Do đó góc giữa hai mặt phẳng (SBC) và (ABCD) bằng $\hat{S M O}$ .

Vì OM là đường trung bình của ∆ABC nên $O M = \frac{A B}{2} = \frac{a}{2}$ .

Xét ∆SOM vuông tại O, có

\tan \hat{S M O} = \frac{S O}{O M} = \sqrt{3} \Rightarrow \hat{S M O} = 60 °

Câu 4:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 2, $B C = 2 \sqrt{3}$ , cạnh bên $S A = \frac{\sqrt{3}}{2}$ và vuông góc với mặt đáy (ABC). Gọi M là trung điểm AB, tính tan của góc giữa hai mặt phẳng (SMC) và mặt đáy (ABC).

A. $\frac{4}{\sqrt{13}}$

B. $\frac{\sqrt{13}}{4}$

C. 1

D. $\frac{\sqrt{2}}{2}$

Xem đáp án

Đáp án đúng là: B

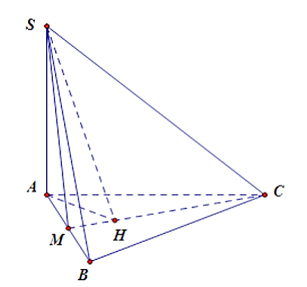
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 2, (ảnh 1)

Vì SA ^ (ABC) nên SA ^ CM.

Kẻ AH ^ CM tại H.

Vì SA ^ CM và AH ^ CM nên CM ^ (SAH) ⇒ CM ^ SH

Do đó góc giữa hai mặt phẳng (SMC) và mặt đáy (ABC) bằng .

Vì M là trung điểm của AB nên $B M = \frac{A B}{2} = 1$ .

Xét ∆CBM vuông tại B, có $C M = \sqrt{B M^{2} + B C^{2}} = \sqrt{1^{2} + {(2 \sqrt{3})}^{2}} = \sqrt{13}$ .

Ta có S_∆ABC = 2S_∆CMA nên $\frac{1}{2} A B . B C = 2. \frac{1}{2} A H . C M \Rightarrow 2 \sqrt{3} = A H . \sqrt{13} \Rightarrow A H = \frac{2 \sqrt{3}}{\sqrt{13}}$ .

Xét ∆SAH vuông tại A, $\tan \hat{S H A} = \frac{S A}{A H} = \frac{\sqrt{13}}{4}$ .

Câu 5:

Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AB = BC = a, $S A = a \sqrt{3}$ , SA ^ (ABC). Góc giữa hai mặt phẳng (SBC) và (ABC) là

A. 45°;

B. 60°;

C. 90°;

D. 30°.

Xem đáp án

Đáp án đúng là: B

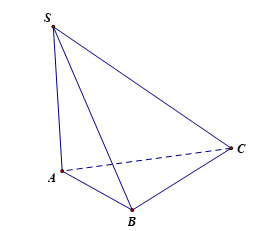
Cho hình chóp S.ABC có tam giác ABC vuông cân tại B, AB = BC = a (ảnh 1)

Vì SA ^ (ABC) nên SA ^ BC mà AB ^ BC (do tam giác ABC vuông cân tại B) nên BC ^ (SAB) ⇒ BC ^ SB.

Do đó góc giữa hai mặt phẳng (SBC) và (ABC) là $\hat{S B A}$ .

Xét ∆SAB vuông tại A, $\tan \hat{S B A} = \frac{S A}{A B} = \frac{a \sqrt{3}}{a} = \sqrt{3} \Rightarrow \hat{S B A} = 60 °$ .

Câu 6:

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D, AB là đáy lớn và tam giác ABC là cân tại C, AC = a. Các mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy, cạnh bên $S C = a \sqrt{3}$ và tạo với mặt phẳng (SAB) một góc bằng 30°. Góc giữa hai mặt phẳng (SAB) và (SAC) bằng

A. 30°;

B. 60°;

C. 90°;

D. 45°.

Xem đáp án

Đáp án đúng là: B

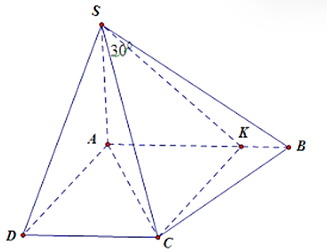
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D, AB là đáy lớn và tam giác ABC là cân tại C, AC = a. (ảnh 1)

Vì $\begin{array}{l} (S A B) ⊥ (A B C D) \\ (S A C) ⊥ (A B C D) \\ (S A B) \cap (S A C) = S A \end{array}\} \Rightarrow S A ⊥ (A B C D)$ .

Kẻ CK ^ AB tại K.

Vì SA ^ (ABCD) nên SA ^ CK mà CK ^ AB nên CK ^ (SAB).

Do đó hình chiếu của SC lên mặt phẳng (SAB) là SK.

Do đó .

Xét ∆SCK vuông tại K, có CK = SC.sin30° = $\frac{a \sqrt{3}}{2}$ .

Vì tam giác ABC cân tại C mà $C K = \frac{a \sqrt{3}}{2}$ nên tam giác ABC đều.

Vì SA ^ (ABCD) nên SA ^ AC, SA ^ AB.

Do đó góc giữa hai mặt phẳng (SAB) và (SAC) bằng $\hat{B A C} = 60 °$ .

Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh SA vuông góc với mặt phẳng đáy, $S A = a \sqrt{3}$ . Góc tạo bởi (SAB) và (SCD) bằng

A. 30°;

B. 60°;

C. 90°;

D. 45°.

Xem đáp án

Đáp án đúng là: A

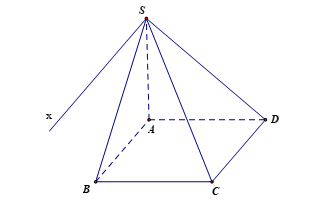
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh SA vuông góc với mặt phẳng đáy (ảnh 1)

Vì $\begin{array}{l} S \in (S A B) \cap (S C D) \\ A B / / C D \end{array}\} \Rightarrow (S A B) \cap (S C D) = S x (S x / / A B / / C D)$ .

Vì SA ^ (ABCD) ⇒ SA ^ AB, SA ^ CD.

Vì SA ^ AB mà AB // Sx nên SA ^ Sx.

Vì SA ^ CD mà CD ^ AD nên CD ^ (SAD) ⇒ CD ^ SD mà CD // Sx nên SD ^ Sx.

Do đó góc tạo bởi (SAB) và (SCD) bằng .

Xét ∆SAD vuông tại A, có $\tan \hat{D S A} = \frac{A D}{S A} = \frac{a}{a \sqrt{3}} = \frac{1}{\sqrt{3}} \Rightarrow \hat{D S A} = 30 °$ .

Câu 8:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a; $A D = \frac{a \sqrt{3}}{2}$ . Mặt bên SAB là tam giác cân đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết . Góc giữa hai mặt phẳng (SAD) và (SBC) bằng:

A. 30°;

B. 60°;

C. 90°;

D. 45°.

Xem đáp án

Đáp án đúng là: B

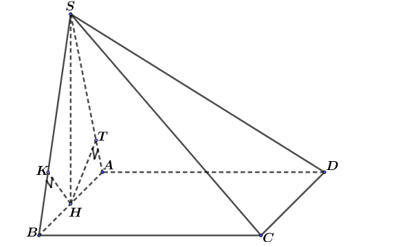
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a (ảnh 1)

Gọi H là trung điểm của AB, theo đề ra ta được SH ^ (ABCD).

Dựng T, K lần lượt là hình chiếu của H lên SA, SB ⇒ HT ^ SA, HK ^ SB.

Vì SH ^ (ABCD) ⇒ SH ^ AD, SH ^ BC.

Vì SH ^ AD mà AD ^ AB ⇒ AD ^ (SAB) ⇒ AD ^ HT

Mà HT ^ SA ⇒ HT ^ (SAD).

Tương tự, HK ^ (SBC).

Do đó góc giữa hai mặt phẳng (SAD) và (SBC) bằng $\hat{K H T}$ .

Vì tứ giác SKHT có $\hat{S K H} + \hat{S T H} = 180 °$ nên tứ giác SKHT là tứ giác nội tiếp.

Suy ra $\hat{K S T} + \hat{K H T} = 180 °$ mà $\hat{K S T} = 120 °$ nên $\hat{K H T} = 60 °$ .

Câu 9:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi có $\hat{B A D} = 120 °$ . Gọi H là trọng tâm của tam giác ABC, hình chiếu vuông góc của điểm S trên mặt phẳng đáy trùng với trọng tâm của tam giác ABC, biết đường cao của khối chóp là $S H = \frac{a \sqrt{6}}{3}$ và tam giác SBD vuông tại S. Tính góc giữa 2 mặt phẳng (SAD) và (SCD).

A. 30°;

B. 60°;

C. 90°;

D. 45°.

Xem đáp án

Đáp án đúng là: C

Câu 10:

Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, cạnh bên SA vuông góc với mặt phẳng đáy, AB = BC = a và SA = a. Góc giữa hai mặt phẳng (SAC) và (SBC) bằng

A. 30°;

B. 60°;

C. 90°;

D. 45°.

Xem đáp án

Đáp án đúng là: B

Gọi H là trung điểm cạnh AC. Suy ra BH ^ AC.

Vì SA ^ (ABC) ⇒ SA ^ BH mà BH ^ AC nên BH ^ (SAC) ⇒ BH ^ SC.

Kẻ HK ^ SC tại K.

Do HK ^ SC và BH ^ SC nên SC ^ (BHK) ⇒ SC ^ BK.

Do đó góc giữa hai mặt phẳng (SAC) và (SBC) bằng $\hat{H K B} = φ$ .

Vì ∆ABC vuông cân tại B nên $B H = \frac{1}{2} A C = \frac{1}{2} \sqrt{A B^{2} + A C^{2}} = \frac{a \sqrt{2}}{2}$ .

Xét ∆SAC vuông tại A, có $S C = \sqrt{S A^{2} + A C^{2}} = \sqrt{a^{2} + 2 a^{2}} = a \sqrt{3}$ .

Vì ∆CKH đồng dạng với ∆CAS (góc - góc) nên $\frac{C H}{C S} = \frac{H K}{S A} \Rightarrow H K = \frac{C H . S A}{C S} = \frac{a \sqrt{6}}{6}$ .

Vì BH ^ (SAC) ⇒ BH ^ HK.

Xét tam giác BHK vuông tại H, có $\tan φ = \frac{B H}{H K} = \sqrt{3} \Rightarrow φ = 60 °$ .

Trắc nghiệm Toán 11 Bài 25. Hai mặt phẳng vuông góc có đáp án

Dạng 1: Xác định và tính góc giữa hai mặt phẳng có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương