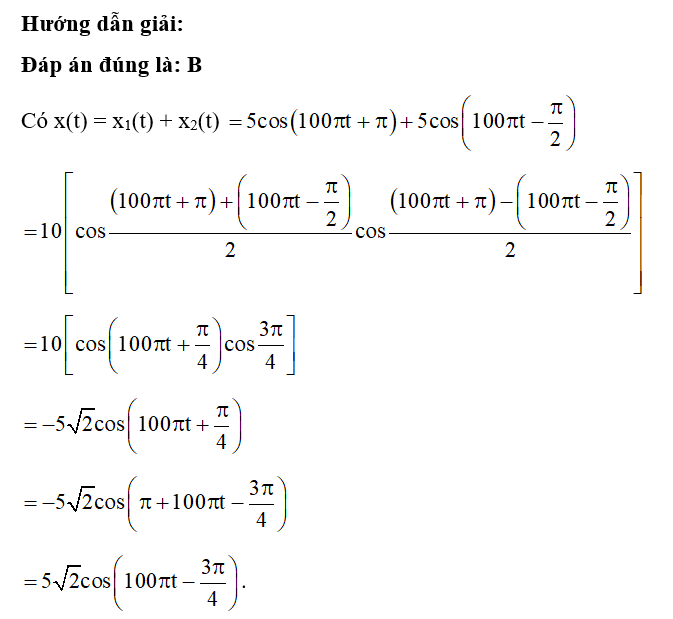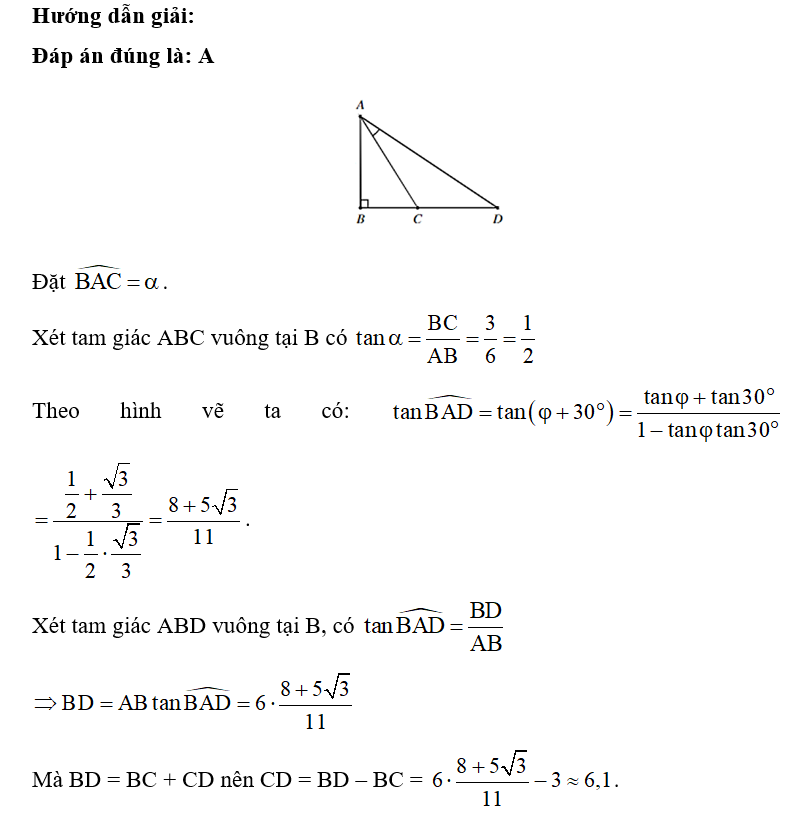10 câu hỏi trắc nghiệm thuộc Dạng 5. Bài toán thực tiễn liên quan

Câu 1:

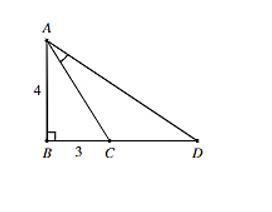
Tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3. Vẽ điểm D nằm trên tia đối của tia CB thỏa mãn $\hat{C A D} = 30 °$ . Tính $\tan \hat{B A D}$ .

Tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3. Vẽ điểm D nằm trên tia đối của (ảnh 1)

A. $\frac{3}{4}$ ;

B. $\frac{48 - 25 \sqrt{3}}{39}$ ;

C. $\frac{48 + 25 \sqrt{3}}{39}$ ;

D. =

\frac{4}{3}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

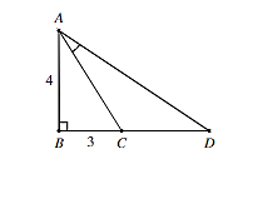
Tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3. Vẽ điểm D nằm trên tia đối của (ảnh 2)

Đặt $\hat{B A C} = φ$ .

Xét tam giác ABC vuông tại B, có $\tan φ = \frac{B C}{A B} = \frac{3}{4}$ .

Theo hình vẽ, ta có

$\tan \hat{B A D} = \tan (φ + 30 °) = \frac{\tan φ + \tan 30 °}{1 - \tan φ \tan 30 °} = \frac{\frac{3}{4} + \frac{\sqrt{3}}{3}}{1 - \frac{3}{4} \cdot \frac{\sqrt{3}}{3}} = \frac{48 + 25 \sqrt{3}}{39}$ .

Câu 2:

Dao động của một vật là tổng hợp của hai dao động điều hòa cùng phương, có phương trình lần lượt là x₁ = 6cos100πt (mm) và x₂ = 6sin100πt (mm), (t tính bằng giây). Tính li độ của vật tại thời điểm t = 0,25 giây.

A. 6;

B. −6;

C. 12;

D. −12.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Ta có x(t) = x₁(t) + x₂(t) = 6cos100πt + 6sin100πt

= $6 [c o s 100 π t + c o s (\frac{π}{2} - 100 π t)]$

$= 12 [c o s \frac{100 π t + (\frac{π}{2} - 100 π t)}{2} c o s \frac{100 π t - (\frac{π}{2} - 100 π t)}{2}]$

$= 12 [c o s \frac{π}{4} c o s (100 π t - \frac{π}{4})] = 6 \sqrt{2} c o s (100 π t - \frac{π}{4})$ .

Có x(0,25) = $= 6 \sqrt{2} c o s \frac{99 π}{4} = - 6$ .

Câu 3:

Cho hai dao động điều hòa cùng phương có phương trình lần lượt là x₁ = 5cos(100πt + π) (cm) và $x_{2} = 5 c o s (100 π t - \frac{π}{2})$ (cm). Phương trình dao động tổng hợp của hai dao động trên là

A. $5 \sqrt{2} c o s (100 π t + \frac{3 π}{4})$ (cm);

B. $5 \sqrt{2} c o s (100 π t - \frac{3 π}{4})$ (cm);

C. $10 c o s (100 π t - \frac{3 π}{4})$ (cm);

D.

10 c o s (100 π t + \frac{3 π}{4})

(cm).

Xem đáp án

Cho hai dao động điều hòa cùng phương có phương trình lần lượt là x1 = 5cos(100 pi t + pi) (cm) (ảnh 1)

Câu 4:

Một vật thực hiện đồng thời hai dao động điều hòa cùng phương, cùng tần số theo các phương trình $x_{1} = 2 c o s (5 π t + \frac{π}{2})$ (cm); x₂ = 2cos5πt (cm). Biên độ của dao động tổng hợp của hai dao động trên là

A. 2;

B. 4;

C. $2 \sqrt{2}$ ;

D.

\sqrt{2}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Có x(t) = $2 c o s (5 π t + \frac{π}{2}) + 2 c o s 5 π t$

$= 4 c o s \frac{(5 π t + \frac{π}{2}) + 5 π t}{2} c o s \frac{(5 π t + \frac{π}{2}) - 5 π t}{2}$

$= 4 c o s (5 π t + \frac{π}{4}) c o s \frac{π}{4}$

$= 2 \sqrt{2} c o s (5 π t + \frac{π}{4})$ .

Vậy $A = 2 \sqrt{2}$ .

Câu 5:

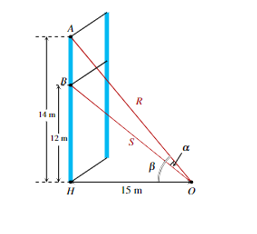
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Biết rằng hai sợi cáp trên cùng được gắn với mặt đất tại một vị trí cách chân cột 15 m. Tính tanα (α là góc giữa hai sợi dây cáp trên).

Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác (ảnh 1)

A. $\frac{14}{15}$ ;

B. $\frac{12}{15}$ ;

C. $\frac{10}{131}$ ;

D.

\frac{130}{19}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Đặt $\hat{H O A} = β$ và $\hat{H O B} = β_{1}$ .

Xét tam giác HOB vuông tại H, có $\tan β_{1} = \frac{H B}{H O} = \frac{12}{15} = \frac{4}{5}$ .

Xét tam giác HOA vuông tại H, có $\tan β = \frac{H A}{H O} = \frac{14}{15}$ .

Theo hình vẽ, ta có tanα = tan(β – β₁) = $\frac{\tan β - \tan β_{1}}{1 + \tan β \tan β_{1}}$ $= \frac{\frac{14}{15} - \frac{4}{5}}{1 + \frac{14}{15} \cdot \frac{4}{5}} = \frac{10}{131}$ .

Câu 6:

Một vật thực hiện đồng thời hai dao động điều hòa có phương trình $x_{1} (t) = 2 \sqrt{3} \sin (4 π t + \frac{π}{6})$ và $x_{2} (t) = 2 c o s (4 π t + \frac{π}{6})$ . Biết rằng phương trình dao động tổng hợp của vật đó x(t) = x₁(t) + x₂(t) viết được dưới dạng x(t) = Acos(ωt + φ). Xác định ω.

A. $\frac{π}{6}$ ;

B. $- \frac{π}{6}$ ;

C. 4π;

D. 4πt.

Xem đáp án

Một vật thực hiện đồng thời hai dao động điều hòa có phương trình (ảnh 1)

Câu 7:

Một vật thực hiện đồng thời hai dao động điều hòa có phương trình $x_{1} (t) = \sin (π t + \frac{π}{3})$ và $x_{2} (t) = c o s (π t + \frac{π}{3})$ . Phương trình dao động tổng hợp của vật x(t) = x₁(t) + x₂(t) được viết dưới dạng x(t) = Acos(ωt + φ), tức là dao động tổng hợp của vật đó là dao động điều hòa. Hãy xác định pha ban đầu φ (−π < φ < π) của dao động tổng hợp.

A. $\frac{π}{4}$ ;

B. $\frac{π}{12}$ ;

C. $\frac{5 π}{12}$ ;

D.

- \frac{π}{4}

.

Xem đáp án

Câu 8:

Hiệu điện thế và cường độ dòng điện trong một thiết bị điện lần lượt được cho bởi các biểu thức sau: u = 40sin(120πt) + 10sin(360πt) (V) và i = 4sin(120πt) + sin(360πt) (A).

(Nguồn: Ron Larson, Intermediate Algebra, Cengage)

Biết rằng công suất tiêu thụ tức thời của thiết bị đó được tính theo công thức P = u∙i (W). Hãy viết biểu thức biểu thị công suất tiêu thụ tức thời ở dạng không có lũy thừa và tích của các biểu thức lượng giác.

A. 85 − 40cos(240πt) − 40cos(480πt) – cos(720πt);

B. 85 − 40cos(240πt) − 40cos(480πt) – 5cos(360πt);

C. 80 − 40cos(240πt) − 40cos(480πt) – 5cos(720πt);

D. 85 − 40cos(240πt) − 40cos(480πt) – 5cos(720πt).

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Ta có P = u∙i = [40sin(120πt) + 10sin(360πt)][4sin(120πt) + sin(360πt)]

= 160sin²(120πt) + 80sin(120πt)sin(360πt) + 10sin²(360πt)

= 80(1 – cos(240πt)) + 40(cos(240πt) – cos(480πt)) + 5(1 – cos(720πt))

= 80 – 80cos(240πt) + 40cos(240πt) − 40cos(480πt) + 5 – 5cos(720πt)

= 85 − 40cos(240πt) − 40cos(480πt) – 5cos(720πt).

Câu 9:

Một quả bóng golf kể từ lúc được đánh đến lúc chạm đất đã di chuyển được một khoảng cách d (m) theo phương nằm ngang. Biết rằng $d = \frac{v_{0}^{2} \sin 2 α}{g}$ trong đó v₀ (m/s) là vận tốc ban đầu của quả bóng, g (m/s²) là gia tốc trọng trường và α là góc đánh quả bóng so với phương nằm ngang. Biết rằng v₀ = 15 (m/s); g = 10 (m/s²) và $cos α = \frac{3}{5}$ với (0 ≤ $α$ ≤ 45°).

Một quả bóng golf kể từ lúc được đánh đến lúc chạm đất đã di chuyển được một khoảng cách (ảnh 1)

Khoảng cách d là

A. 20 cm;

B. $\frac{105}{6}$ cm;

C. 25 cm

D.

\frac{108}{6}

cm.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Vì sin²α + cos²α = 1 mà $cos α = \frac{3}{5}$ nên $\sin^{2} α = \frac{16}{25}$ .

Vì 0 ≤ α ≤ 45° nên sinα > 0, suy ra $\sin α = \frac{4}{5}$ .

Ta có $d = \frac{v_{0}^{2} \sin 2 α}{g} d = \frac{2 v_{0}^{2} \sin α c o s α}{g} = \frac{2 \cdot 15^{2} \cdot \frac{4}{5} \cdot \frac{3}{5}}{10} = \frac{108}{5}$ (cm).

Câu 10:

Tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 6, BC = 3. Vẽ điểm D nằm trên tia đối của tia CB thỏa mãn $\hat{C A D} = 30 °$ . Tính CD (làm tròn kết quả đến số thập phân thứ nhất)

A. 6,1

B. 6,02

C. 6

D.

\frac{4}{3}

.

Xem đáp án

Trắc nghiệm Toán 11 Bài 2. Công thức lượng giác có đáp án

Dạng 5. Bài toán thực tiễn liên quan

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương