Dạng 3: Các bài toán liên quan đến tính chất của hình lăng trụ và hình hộp có đáp án
-
159 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Hai mặt đáy của hình lăng trụ
Xem đáp án
Đáp án đúng là: A
Hai mặt đáy của hình lăng trụ song song với nhau.
Câu 2:
Các cạnh bên của hình lăng trụ
Xem đáp án
Đáp án đúng là: C
Các cạnh bên của hình lăng trụ song song với nhau và có độ dài bằng nhau.
Câu 3:
Các mặt bên của hình lăng trụ là
Xem đáp án
Đáp án đúng là: D
Các mặt bên của hình lăng trụ là hình bình hành.
Câu 4:
Khẳng định nào sau đây là đúng
Xem đáp án
Đáp án đúng là: D
Hình hộp là hình lăng trụ có 2 đáy là hình bình hành nên có 8 đỉnh.
Các mặt đối điện của hình hộp song song với nhau và các cạnh bên của hình hộp song song với nhau.
Câu 6:
Các đường chéo của hình hộp
A. Tạo thành một tam giác đều;
B. Tạo thành một tam giác cân;
C. Tạo thành một tam giác;
D. Đồng quy tại trung điểm mỗi đường.
Xem đáp án
Đáp án đúng là: D
Các đường chéo của hình hộp đồng quy tại trung điểm mỗi đường.
Câu 7:
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Khi đó ABCD.MNPQ là hình gì?
Xem đáp án
Đáp án đúng là: D
Câu 8:
Cho hình lăng trụ ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của các cạnh AB, A’B’. MNC’C là
Xem đáp án
Đáp án đúng là: C
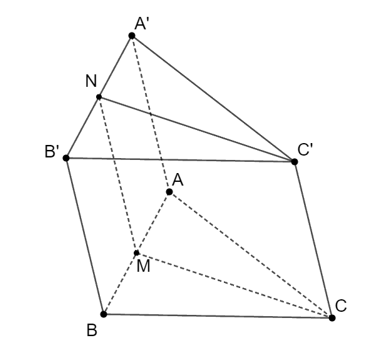
Hình bình hành ABB’A’ có: M, N là trung điểm AB, A’B’.
Suy ra MN là đường trung bình của hình bình hành ABB’A’.
Do đó MN // BB’ và MN = BB’.
Mà BB’ // CC’ và BB’ = CC’ (do tứ giác BCC’B’ là hình bình hành).
Suy ra MN // CC’ và MN = CC’.
Vậy tứ giác MNC’C là hình bình hành.
Câu 9:
Cho hình lăng trụ ABC.A’B’C’. Gọi G là trọng tâm của các tam giác ABC. Lấy điểm M trên cạnh AC sao cho AM = 2MC. Vị trí tương đối của GM và (BCC’B’) là
Xem đáp án
Đáp án đúng là: A
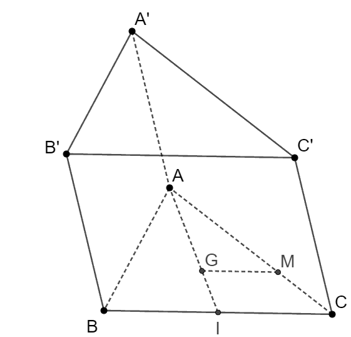
Gọi I là trung điểm BC.
Vì G là trọng tâm của tam giác ABC nên .
Lại có AM = 2MC, suy ra .
Khi đó .
Áp dụng định lí Thalès đảo, ta được GM // BC.
Suy ra GM // (BCC’B’)
Câu 10:
Cho hình hộp ABCD.A’B’C’D’. Gọi giao điểm của AC và BD là O; giao điểm của A’C’ và B’D’ là O’. Vị trí tương đối của (O’AB) và (OC’D’) là
Xem đáp án
Đáp án đúng là: B
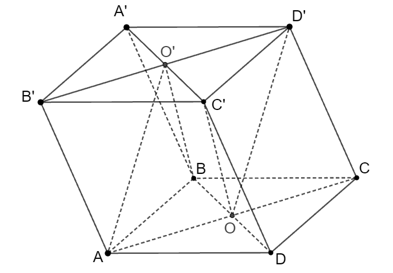
Ta có AB // C’D’ (hai cạnh đối diện của hình hộp)
Do đó AB // (OC’D’) (1)
Ta có AA’ // CC’ và AA’ = CC’.
Suy ra tứ giác ACC’A’ là hình bình hành.
Do đó A’C’ // AC và A’C’ = AC.
Mà O, O’ lần lượt là trung điểm của AC và A’C’.
Suy ra O’C’ // AO và O’C’ = AO.
Vì vậy tứ giác AOC’O’ là hình bình hành.
Do đó O’A // OC’.
Suy ra O’A // (OC’D’) (2)
Trong (O’AB): O’A ∩ AB = A (3)
Từ (1), (2), (3), ta thu được (O’AB) // (OC’D’).