Câu hỏi:
12/03/2024 36
Cho hình lăng trụ ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của các cạnh AB, A’B’. MNC’C là
Cho hình lăng trụ ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của các cạnh AB, A’B’. MNC’C là
A. Hình tứ giác;
B. Hình chữ nhật;
C. Hình bình hành;
D. Hình thoi.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
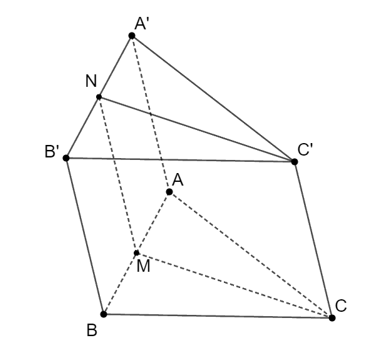
Hình bình hành ABB’A’ có: M, N là trung điểm AB, A’B’.
Suy ra MN là đường trung bình của hình bình hành ABB’A’.
Do đó MN // BB’ và MN = BB’.
Mà BB’ // CC’ và BB’ = CC’ (do tứ giác BCC’B’ là hình bình hành).
Suy ra MN // CC’ và MN = CC’.
Vậy tứ giác MNC’C là hình bình hành.
Đáp án đúng là: C

Hình bình hành ABB’A’ có: M, N là trung điểm AB, A’B’.
Suy ra MN là đường trung bình của hình bình hành ABB’A’.
Do đó MN // BB’ và MN = BB’.
Mà BB’ // CC’ và BB’ = CC’ (do tứ giác BCC’B’ là hình bình hành).
Suy ra MN // CC’ và MN = CC’.
Vậy tứ giác MNC’C là hình bình hành.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho hình lăng trụ ABC.A’B’C’. Gọi G là trọng tâm của các tam giác ABC. Lấy điểm M trên cạnh AC sao cho AM = 2MC. Vị trí tương đối của GM và (BCC’B’) là
Cho hình lăng trụ ABC.A’B’C’. Gọi G là trọng tâm của các tam giác ABC. Lấy điểm M trên cạnh AC sao cho AM = 2MC. Vị trí tương đối của GM và (BCC’B’) là
Câu 3:
Các đường chéo của hình hộp
A. Tạo thành một tam giác đều;
B. Tạo thành một tam giác cân;
C. Tạo thành một tam giác;
D. Đồng quy tại trung điểm mỗi đường.
Các đường chéo của hình hộp
A. Tạo thành một tam giác đều;
B. Tạo thành một tam giác cân;
C. Tạo thành một tam giác;
D. Đồng quy tại trung điểm mỗi đường.
Câu 4:
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Khi đó ABCD.MNPQ là hình gì?
Cho hình lăng trụ tứ giác ABCD.A’B’C’D’. Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Khi đó ABCD.MNPQ là hình gì?
Câu 5:
Cho hình hộp ABCD.A’B’C’D’. Gọi giao điểm của AC và BD là O; giao điểm của A’C’ và B’D’ là O’. Vị trí tương đối của (O’AB) và (OC’D’) là
Cho hình hộp ABCD.A’B’C’D’. Gọi giao điểm của AC và BD là O; giao điểm của A’C’ và B’D’ là O’. Vị trí tương đối của (O’AB) và (OC’D’) là


