Dạng 1: Xác định, chứng minh hai mặt phẳng song song có đáp án
-
160 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho hai mặt phẳng song song (P) và (Q). Đường thẳng d nằm trên (P). Số điểm chung của mặt phẳng (Q) và d là
Xem đáp án
Đáp án đúng là: A
Vì (P) và (Q) song song mà d nằm trên (P) nên d song song với (Q).
Vậy d và (Q) không có điểm chung.
Câu 2:
Cho tứ diện SABC. D, E, F là trung điểm các cạnh SA, SB, SC. Vị trí tương đối của (DEF) và (ABC) là
Xem đáp án
Đáp án đúng là: A
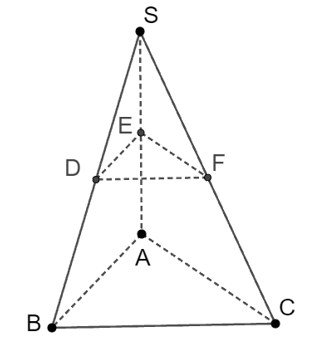
D, E, F là trung điểm các đoạn thẳng SA, SB, SC nên DE // AB, EF // AC, EF // BC (tính chất đường trung bình của tam giác).
Do đó DE, EF, EF đều song song với (ABC).
Vậy (DEF) // (ABC).
Câu 3:
Cho hình bình hành ABCD và điểm S không nằm trên (ABCD). O là giao điểm của AC và BD. Gọi E, F, H theo thứ tự là trung điểm của SA; SD và AB. Khẳng định đúng trong các khẳng định sau là
Xem đáp án
Đáp án đúng là: B
Ta có EF là đường trung bình của tam giác SAD suy ra: EF // AD (1).
OH là đường trung bình của tam giác ABC suy ra: OH // BC // AD (2).
Từ (1) và (2) suy ra : EF // OH // AD nên 4 điểm E; F; O; H đồng phẳng
Lại có: EH // SB; OH // BC; EH, OH ⊂ (EFOH) và SB, SC ⊂ (SBC) nên (EFOH) // (SBC) hay (EOF) // (SBC).
Câu 4:
Cho hình bình hành ABCD và điểm S không nằm trên (ABCD). O là giao điểm của AC và BD. E và F lần lượt là trung điểm của SA; SD. Khẳng định sai trong các khẳng định sau là
Xem đáp án
Đáp án đúng là: D
Câu 5:
Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh SA, SB, SC và SD. Khẳng định sai trong các khẳng định sau là
Xem đáp án
Đáp án đúng là: C
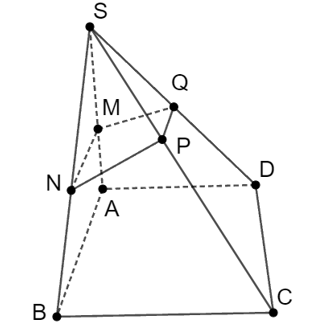
* Xét khẳng định: MN // (ABCD)
Do M và N lần lượt là trung điểm của SA và SB
⇒ MN là đường trung bình của tam giác SAB và MN // AB.
Mà AB ⊂ (ABCD) nên MN // (ABCD) (1)
⇒ A đúng.
* Xét khẳng định: MP // (ABCD).
Do M và P lần lượt là trung điểm của SA và SC
⇒ MP là đường trung bình của tam giác SAC và MP // AC
Mà AC ⊂ (ABCD) nên MP // (ABCD) (2)
⇒ B đúng.
Từ (1) và (2) và kết hợp với MN và MP là hai đường thẳng cắt nhau tại M và cùng thuộc (MNPQ) ta suy ra: (ABCD) // (MNPQ)
⇒ D đúng.
Vậy khẳng định sai là C.
Câu 6:
Cho hình bình hành ABCD và điểm S không nằm trên (ABCD). O là giao điểm của AC và BD. M, N, I là trung điểm của SA, SD, AB. Vị trí tương đối của (MON) và (SBC) là
Xem đáp án
Đáp án đúng là: B
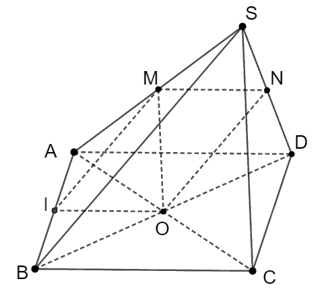
Ta có MN là đường trung bình của tam giác SAD suy ra: MN // AD (1).
OI là đường trung bình của tam giác ABC suy ra: OI // BC // AD (2).
Từ (1) và (2) suy ra : MN // OI // AD nên 4 điểm M, N, O, I đồng phẳng.
Lại có: MI // SB; OI // BC; MI, OI ⊂ (MNOI) và SB, SC ⊂ (SBC) nên (MNOI) // (SBC) hay (MON) // (SBC).
Câu 7:
Hai hình vuông ABCD và ABEF nằm ở hai mặt phẳng khác nhau. Vị trí tương đối của (CBE) và (ADF) là
Xem đáp án
Đáp án đúng là: A
• ABCD là hình vuông nên AD // BC.
• ABEF là hình vuông nên AF // BE.
Do nên (CBE) // (ADF).
Câu 8:
Cho hình bình hành ABCD và điểm S không nằm trên (ABCD). O là giao điểm của AC và BD. Mặt phẳng (P) qua BD và song song với SA, cắt SC tại I. Khẳng định đúng trong các khẳng định sau là
Xem đáp án
Đáp án đúng là: D
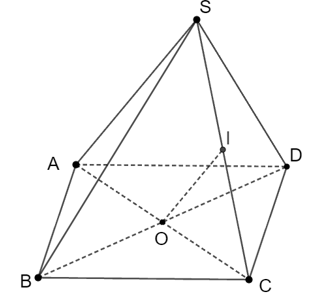
Gọi O là giao điểm của AC và BD.
Do mặt phẳng (α) qua BD nên O ∈ (α)
• Trong tam giác SAC, kẻ OI // SA (k ∈ SC).
Do .
• Trong tam giác SAC ta có:
là đường trung bình của ΔSAC.
Vậy SI = IC.
Câu 9:
Cho hình chóp S.ABC; gọi G, H là trọng tâm tam giác SAC và SBC. Gọi M là trung điểm của BC. Đường thẳng song song với (ABC) là
Xem đáp án
Đáp án đúng là: C
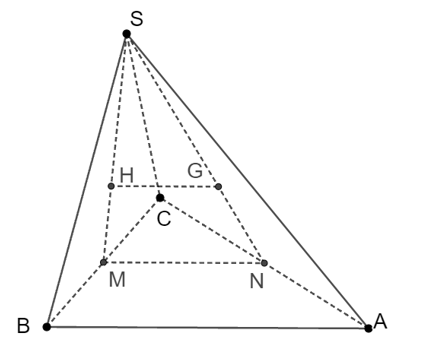
Gọi M và N là trung điểm của BC và AC.
Do G, H lần lượt là trọng tâm tam giác SAC và SBC nên:
.
Suy ra GH // HK.
Mà HK ⊂ (ABC) nên GH // (ABC).
Câu 10:
Cho hình chóp S.ABCD có đáy là hình thang (AD // BC, AD > BC). Gọi M, N, E lần lượt là trung điểm của AB, CD, SA. Vị trí tương đối của (MEN) và (SBC) là
Xem đáp án
Đáp án đúng là: A
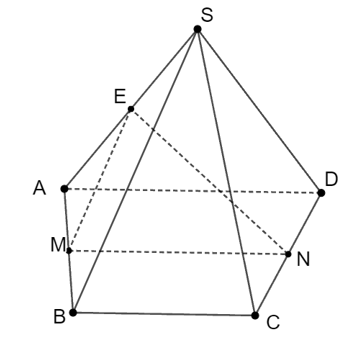
Ta có MN // BC mà BC ⊂ (SBC) nên MN // (SBC).
Do MN // BC, ME // (SBC) nên (MEN) // (SBC).