Trắc nghiệm Toán 10 CTST Bài 1. Bất phương trình bậc nhất hai ẩn có đáp án (Phần 2)
Trắc nghiệm Toán 10 CTST Bài 1. Bất phương trình bậc nhất hai ẩn có đáp án (Vận dụng)
-
212 lượt thi
-
5 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Thời gian tối đa để hoàn thiện:
+ Kệ sách là: 240 : 4 = 60 giờ.
+ Bàn: 240 : 3 = 80 giờ.
Khi đó ta có:
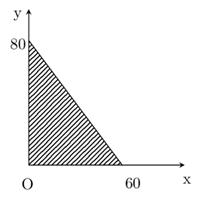
Câu 2:
Cho bất phương trình 2x + y – 6 < 0 (1). Điểm A là giao điểm của parabol (P) y = x2 và đường thẳng y = 5x – 4 . Biết A thuộc miền nghiệm của bất phương trình (1). Có bao nhiêu điểm A thỏa mãn?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Điểm A là giao điểm của parabol (P) y = x2 và đường thẳng y = 5x – 4 nên hoành độ của điểm A là nghiệm của phương trình:
x2 = 5x – 4 Û x2 – 5x + 4 = 0 Û \(\left[ \begin{array}{l}x = 1\\x = 4\end{array} \right.\)
Khi đó ta được hai điểm (1; 1) và (4; 16).
Xét điểm (1; 1) ta có: 2.1 + 1 – 6 = –3 < 0 nên (1; 1) là nghiệm của bất phương trình (1) do đó điểm A(1; 1) thuộc miền nghiệm của bất phương trình (1).
Xét điểm (4; 16) ta có: 2.4 + 16 – 6 = 18 > 0 nên (4; 16) không là nghiệm của bất phương trình (1) do đó điểm (4; 16) không thuộc miền nghiệm của bất phương trình (1).
Vậy có 1 điểm A(1; 1) thỏa mãn.
Câu 3:
Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:
|
Nhóm |
Số máy trong mỗi nhóm |
Số máy trong từng nhóm để sản xuất ra một đơn vị sản phẩm |
|
|
Loại I |
Loại II |
||
|
A |
10 |
2 |
2 |
|
B |
4 |
0 |
2 |
|
C |
12 |
2 |
4 |
Gọi x, y (x, y ≥ 0) lần lượt là số đơn vị sản phẩm loại I và loại II sản xuất. Các bất phương trình mô tả số đơn vị sản phẩm loại I và loại II sản xuất là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Để sản xuất một đơn vị sản phẩm loại I thì cần 2 máy nhóm A và 2 máy nhóm C nên để sản xuất x đơn vị sản phẩm loại I thì cần 2x máy nhóm A và 2x máy nhóm C.
Để sản xuất một đơn vị sản phẩm loại II thì cần 2 máy nhóm A, 2 máy nhóm B và 4 máy nhóm C nên để sản xuất y đơn vị sản phẩm loại II thì cần 2y máy nhóm A, 2y máy nhóm B và 4y máy nhóm C.
Mà có tất cả 10 máy nhóm A nên ta có: 2x + 2y ≤ 10 Û x + y – 5 ≤ 0.
Có tất cả 4 máy nhóm B nên ta có: 2y ≤ 4 Û y ≤ 2.
Có tất cả 12 máy nhóm C nên ta có: 2x + 4y ≤ 12 Û x + 2y – 6 ≤ 0.
Vậy ta có các bất phương trình:
x ≥ 0;
0 ≤ y ≤ 2;
x + y – 5 ≤ 0;
x + 2y – 6 ≤ 0.
Ta chọn phương án D.
Câu 4:
Tất cả các giá trị thực của tham số m để bất phương trình 3x + my − 7 ≥ 0 có miền nghiệm chứa điểm A(\(\sqrt 2 \); 1) là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Do điểm A(\(\sqrt 2 \); 1) thuộc miền nghiệm của bất phương trình, thay x = \(\sqrt 2 \) và y = 1 vào bất phương trình ta được:
\(3\sqrt 2 + m - 7 \ge 0 \Leftrightarrow m \ge 7 - 3\sqrt 2 \)
Vậy với \(m \in \left[ {7 - 3\sqrt 2 ; + \infty } \right)\) thì bất phương trình 3x + my − 7 ≥ 0 có miền nghiệm chứa điểm A(\(\sqrt 2 \); 1).
Ta chọn phương án D.
Câu 5:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Ta có: 2x − 3(y − x) > 4 ⇔ 2x – 3y + 3x – 4 > 0 ⇔ 5x – 3y – 4 > 0.
Do điểm A(1 − m; m) không thuộc miền nghiệm của bất phương trình nên thay tọa độ điểm A vào bất phương trình trên không thoả mãn hay điểm A thuộc miền nghiệm của bất phương trình 5x – 3y – 4 ≤ 0.
Khi đó ta có: 5(1 – m) – 3m – 4 ≤ 0
⇔ 5 – 5m – 3m – 4 ≥ 0
⇔ –8m ≥ –1
⇔ m ≤ \(\frac{1}{8}\)
Ta chọn phương án B.