8 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 CTST Bài 1. Bất phương trình bậc nhất hai ẩn có đáp án (Thông hiểu)

Câu 1:

Miền nghiệm của bất phương trình 4(x – 1) + 5(y – 3) > 2x – 9 là nửa mặt phẳng chứa điểm:

A. (0; 0);

B. (1; 1);

C. (–1; 1);

D. (2; 5).

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Ta có: 4(x – 1) + 5(y – 3) > 2x – 9

Û 4x – 4 + 5y – 15 – 2x + 9 > 0

Û 2x + 5y – 10 > 0.

Xét điểm (0; 0) ta có: 2.0 + 5.0 – 10 = –10 < 0 nên (0; 0) không là nghiệm của bất phương trình đã cho.

Xét điểm (1; 1) ta có: 2.1 + 5.1 – 10 = –3 < 0 nên (1; 1) không là nghiệm của bất phương trình đã cho.

Xét điểm (–1; 1) ta có: 2.(–1) + 5.1 – 10 = –7 < 0 nên (–1; 1) không là nghiệm của bất phương trình đã cho.

Xét điểm (2; 5) ta có: 2.2 + 5.5 – 10 = 19 > 0 nên (2; 5) là một nghiệm của bất phương trình đã cho.

Khi đó miền nghiệm của bất phương trình 4(x – 1) + 5(y – 3) > 2x – 9 là nửa mặt phẳng chứa điểm (2; 5).

Câu 2:

Miền nghiệm của bất phương trình x + 3 + 2(2y + 5) < 2(1 – x) là mặt phẳng không chứa điểm

A. (–3; –4);

B. (–2; –5);

C. (0; 0);

D. (–1; –6).

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Ta có: x + 3 + 2(2y + 5) < 2(1 – x) Û 3x + 4y + 11 < 0.

Xét điểm (–3; –4) ta có: 3.(–3) + 4.(–4) + 11 = –14 < 0 nên (–3; –4) là một nghiệm của bất phương trình đã cho.

Xét điểm (–2; –5) ta có: 3.(–2) + 4.(–5) + 11 = –15 < 0 nên (–2; –5) là một nghiệm của bất phương trình đã cho.

Xét điểm (0; 0) ta có: 3.0 + 4.0 + 11 = 11 > 0 nên (0; 0) là không là nghiệm của bất phương trình đã cho.

Xét điểm (–1; –6) ta có: 3.(–1) + 4.(–6) + 11 = –16 < 0 nên (–1; –6) là một nghiệm của bất phương trình đã cho.

Do đó miền nghiệm của bất phương trình đã cho là nửa mặt phẳng không chứa điểm (0; 0).

Vậy ta chọn phương án C.

Câu 3:

Miền nghiệm của bất phương trình 3x – 2y < –6 được biểu diễn bởi miền không tô đậm trong hình vẽ nào dưới đây:

A.

B.

C.

D.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Ta có: 3x – 2y < –6 Û 3x – 2y + 6 < 0.

Trước hết, ta vẽ đường thẳng (d): 3x – 2y + 6 = 0.

Ta thấy (0 ; 0) không phải là nghiệm của bất phương trình đã cho.

Do đó miền nghiệm của bất phương trình là nửa mặt phẳng (không kể bờ (d)) và không chứa điểm (0; 0).

Vậy miền không tô đậm trong hình vẽ là miền nghiệm của bất phương trình.

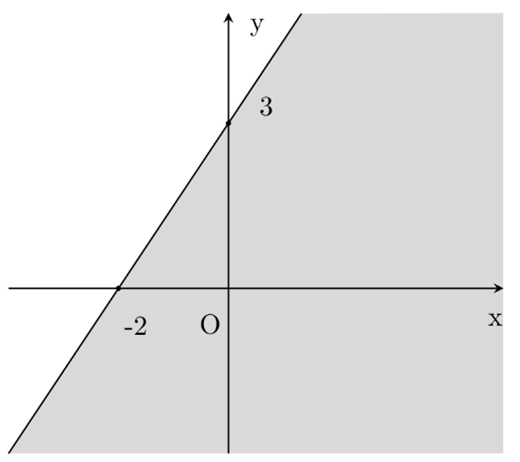
Câu 4:

Miền nghiệm của bất phương trình 3(x – 1) + 3(y + 2) > 5x + 2y + 8 là:

A. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng y = 2x + 5 (không bao gồm đường thẳng);

B. Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng y = 2x + 5 (không bao gồm đường thẳng);

C. Nửa mặt phẳng không chứa gốc tọa độ, bờ là đường thẳng y = 2x + 5 (bao gồm đường thẳng);

D. Nửa mặt phẳng chứa gốc tọa độ, bờ là đường thẳng y = 2x + 5 (bao gồm đường thẳng).

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Ta có: 3(x – 1) + 3(y + 2) > 5x + 2y + 8 Û 2x – y + 5 < 0.

Xét đường thẳng d: 2x – y + 5 = 0 hay y = 2x – 5.

Ta thấy điểm (0; 0) không thuộc d và 2.0 – 0 + 5 = 5 > 0.

Do đó miền nghiệm của bất phương trình đã cho là nửa mặt phẳng không kể bờ d, không chứa gốc toạ độ.

Ta chọn phương án A.

Câu 5:

Một người thợ mộc tốn 6 giờ để làm một cái bàn và 4 giờ để làm một cái ghế. Gọi x, y lần lượt là số bàn và số ghế mà người thợ mộc sản xuất trong một tuần. Viết bất phương trình biểu thị mối liên hệ giữa x và y biết trong một tuần người thợ mộc có thể làm tối đa 50 giờ.

A. 3x + 2y < 25;

B. 3x + 2y > 25;

C. 3x + 2y ≤ 25;

D. 3x + 2y ≥ 25.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Thời gian người thợ mộc làm x cái bàn trong 1 tuần là: 6x (giờ).

Thời gian người thợ mộc làm y cái ghế trong 1 tuần là: 4y (giờ)

Thời gian làm x cái bàn và y cái ghế trong 1 tuần là: 6x + 4y (giờ)

Do trong 1 tuần người thợ mộc có thể làm tối đa 50 giờ nên ta có: 6x + 4y ≤ 50.

Hay 3x + 2y ≤ 25.

Ta chọn phương án C.

Câu 6:

Phần không tô đậm (không kể đường thẳng d) trong hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào?

A. x – 2y > 3;

B. x – 2y < 3;

C. 2x – y > 3;

D. 2x – y < 3.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Ta thấy đường thẳng đi qua 2 điểm $(\frac{3}{2}; 0)$ và (0; –3) nên có phương trình 2x – y – 3 = 0.

Xét cặp số (0; 0) ta có 2.0 – 0 – 3 = –3 < 0.

Quan sát hình vẽ ta thấy điểm (0; 0) không nằm trong miền tô đậm nên là nghiệm của bất phương trình.

Do đó bất phương trình là 2x – y – 3 < 0 hay 2x – y < 3.

Vậy phần không tô đậm (không kể đường thẳng d) ở hình trên biểu diễn miền nghiệm của bất phương trình 2x – y < 3.

Câu 7:

Ngoài giờ học, bạn Nam làm thêm việc phụ bán cơm được 15 nghìn đồng/giờ và phụ bán tạp hóa được 18 nghìn đồng/giờ. Gọi x, y lần lượt là số giờ phụ bán cơm và phụ bán tạp hóa trong mỗi tuần. Viết bất phương trình bậc nhất hai ẩn x và y biết Nam làm thêm được số tiền mỗi tuần ít nhất là 900 nghìn đồng.

A. 5x + 6y ≤ 300;

B. 5x + 6y > 300;

C. 5x + 6y ≥ 300;

D. 5x + 6y < 300.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Trong 1 tuần, số tiền Nam làm thêm được khi:

+ Phụ bán cơm: 15x (nghìn đồng)

+ Phụ bán tạp hoá: 18x (nghìn đồng)

Số tiền Nam kiếm thêm được trong 1 tuần là: 15x + 18y (nghìn đồng)

Do Nam làm được ít nhất 900 nghìn đồng 1 tuần nên 15x + 18y ≥ 900.

Hay 5x + 6y ≥ 300.

Ta chọn phương án C.

Câu 8:

Một gian hàng trưng bày bàn và ghế rộng 60 m². Diện tích để kê một chiếc ghế là 0,6 m², một chiếc bàn là 1,3 m². Gọi x là số chiếc ghế, y là số chiếc bàn được kê. Viết bất phương trình bậc nhất hai ẩn x, y cho phần mặt sàn để kê bàn và ghế, biết diện tích mặt sàn dành cho lưu thông tối thiểu là 10 m².

A. 0,6x + 1,3y ≥ 50.

B. 0,6x + 1,3y ≤ 50.

C. 1,3x + 0,6y ≤ 50.

D. 1,3x + 0,6y ≥ 50.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Diện tích kê x chiếc ghế là 0,6x (m²).

Diện tích kê y chiếc bàn là 1,3y (m²).

Tổng diện tích kê bàn ghế là 0,6x + 1,3y (m²).

Do diện tích mặt sàn dành cho lưu thông tối thiểu là 10m² nên diện tích kê bàn và ghế chỉ còn lại tối đa là 60 – 10 = 50 (m²).

Diện tích phần mặt sàn để kê bàn và ghế được biểu diễn là 0,6x + 1,3y ≤ 50.

Ta chọn phương án B.

Trắc nghiệm Toán 10 CTST Bài 1. Bất phương trình bậc nhất hai ẩn có đáp án (Phần 2)

Trắc nghiệm Toán 10 CTST Bài 1. Bất phương trình bậc nhất hai ẩn có đáp án (Thông hiểu)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương