Trắc nghiệm Toán 10 Bài 2. Đường thẳng trong mặt phẳng tọa độ có đáp án
Trắc nghiệm Toán 10 Bài 2. Đường thẳng trong mặt phẳng tọa độ có đáp án
-
238 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Một đường thẳng có bao nhiêu vectơ pháp tuyến?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có được gọi là vectơ pháp tuyến của đường thẳng ∆ nếu và vuông góc với vectơ chỉ phương của đường thẳng ∆.
Có vô số vectơ khác và vuông góc với vectơ chỉ phương của đường thẳng ∆.
Do đó đường thẳng ∆ có vô số vectơ pháp tuyến.
Vậy ta chọn phương án D.
Câu 2:
Đường thẳng d có một vectơ chỉ phương là . Đường thẳng ∆ vuông góc với d có một vectơ pháp tuyến là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
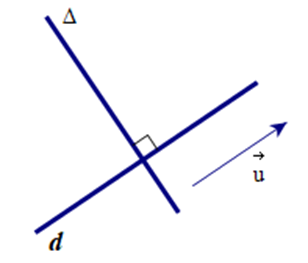
Vì ∆ ⊥ d nên ∆ nhận vectơ chỉ phương của d là một vectơ pháp tuyến.
Suy ra ∆ có vectơ pháp tuyến
Vậy ta chọn phương ánCâu 3:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường thẳng ∆ có một vectơ chỉ phương là
Các vectơ chỉ phương còn lại của đường thẳng ∆ sẽ cùng phương với .
• Ở phương án A, ta có nên cùng phương với
Do đó cũng là một vectơ chỉ phương của ∆.
• Ở phương án B, ta có nên không cùng phương với .
Do đó không là một vectơ chỉ phương của ∆.
• Tương tự, ta có không là vectơ chỉ phương của ∆.
Vậy ta chọn phương án A.
Câu 4:
Cho hai điểm A(4; 0), B(0; 5). Phương trình nào sau đây không phải là phương trình của đường thẳng AB?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
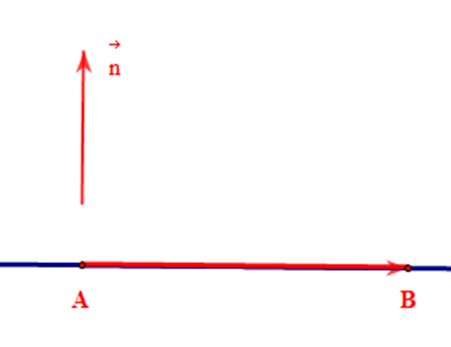
Với A(4; 0), B(0; 5) ta có:
• Đường thẳng AB là đường thẳng đi qua hai điểm A và B, do đó nhận làm vectơ chỉ phương.
Khi đó đường thẳng AB nhận làm vectơ pháp tuyến.
Đường thẳng AB đi qua điểm A(4; 0), có vectơ pháp tuyến nên có phương trình tổng quát là: 5(x – 4) + 4(y – 0) = 0
⇔ 5x + 4y – 20 = 0 ⇔ 4y = –5x + 20 ⇔
Do đó phương trình ở phương án A không phải phương trình AB.
Đến đây ta có thể chọn phương án A.
• Đường thẳng AB đi qua hai điểm A(4; 0), B(0; 5) nên có phương trình đoạn chắn của là:
Do đó phương án B đúng.
• Phương trình đường thẳng AB đi qua hai điểm A(4; 0), B(0; 5) là:
Do đó phương án C đúng.
• Đường thẳng AB đi qua điểm A(4; 0), có vectơ chỉ phương nên có phương trình tham số là:
Do đó phương án D đúng.
Vậy ta chọn phương án A.
Câu 5:
Giao điểm M của hai đường thẳng (d): và (d’): 3x – 2y – 1 = 0 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Đường thẳng (d):
(d) có vectơ chỉ phương
Suy ra (d) có vectơ pháp tuyến
(d) đi qua A(1; –3), có vectơ pháp tuyến nên có phương trình tổng quát là:
5(x – 1) + 2(y + 3) = 0
⇔ 5x + 2y + 1 = 0.
Ta có M là giao điểm của (d) và (d’) nên tọa độ M là nghiệm của hệ phương trình:
Khi đó ta có
Vậy ta chọn phương án B.
Câu 6:
Cho hai đường thẳng ∆1: 11x – 12y + 1 = 0 và ∆2: 12x + 11y + 9 = 0. Khi đó hai đường thẳng này
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hai đường thẳng ∆1, ∆2 có vectơ pháp tuyến lần lượt là ,
Ta có
Suy ra
Khi đó ta có ∆1 ⊥ ∆2.
Vậy ta chọn phương án C.
Câu 7:
Cho ∆ABC có A(2; –1), B(4; 5), C(–3; 2). Phương trình nào sau đây là phương trình tổng quát của đường cao AH?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A

Vì AH là đường cao của ∆ABC nên AH ⊥ BC.
Suy ra
Do đó đường thẳng AH nhận làm vectơ pháp tuyến.
Với B(4; 5), C(–3; 2) ta có
Đường thẳng AH đi qua điểm A(2; –1), có vectơ pháp tuyến
Suy ra phương trình tổng quát của đường thẳng AH là:
–7.(x – 2) – 3.(y + 1) = 0
⇔ –7x – 3y + 11 = 0 ⇔ 7x + 3y – 11 = 0.
Vậy ta chọn phương án A.
Câu 8:
Cho hai điểm A(–2; 3) và B(4; –1). Phương trình đường trung trực của đoạn thẳng AB là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
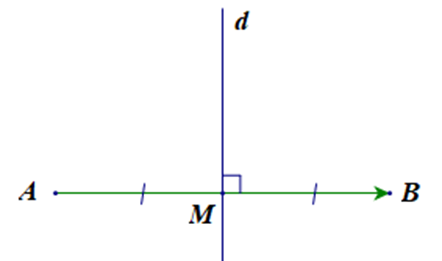
Gọi d là đường trung trực của đoạn thẳng AB.
Gọi M là trung điểm của AB với A(–2; 3) và B(4; –1).
Ta suy ra
Khi đó ta có M(1; 1).
Với A(–2; 3) và B(4; –1) ta có:
Đường thẳng d là đường trung trực của AB nên đường thẳng d đi qua trung điểm M(1; 1) của AB và nhận làm vectơ pháp tuyến.
Suy ra phương trình tổng quát của d là:
6(x – 1) – 4(y – 1) = 0
⇔ 6x – 4y – 2 = 0 ⇔ 3x – 2y – 1 = 0.
Vậy ta chọn phương án C.Câu 9:
Điểm nằm trên đường thẳng ∆: 2x + y – 1 = 0 và có khoảng cách đến (d): 4x + 3y – 10 = 0 bằng 2 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi M(xM; yM) là điểm cần tìm.
Ta có M ∈ ∆. Suy ra 2xM + yM – 1 = 0 ⇔ yM = 1 – 2xM.
Khi đó tọa độ M có dạng: M(xM; 1 – 2xM).
Theo đề ta có khoảng cách từ M đến (d) bằng 2, tức là d(M, (d)) = 2.
Ta suy ra
⇔ |–2xM – 7| = 10
⇔ –2xM – 7 = 10 hoặc –2xM – 7 = –10
⇔ –2xM = 17 hoặc –2xM = –3
.
• Với , ta có: yM = 1 – 2xM = 18.
Suy ra tọa độ
• Với , ta có yM = 1 – 2xM = –2.
Suy ra tọa độ
Vậy có hai điểm M thỏa yêu cầu bài toán là
Do đó ta chọn phương án C.
Câu 10:
Tìm m để góc tạo bởi hai đường thẳng và ∆2: mx + y + 1 = 0 một góc bằng 30°.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
có vectơ pháp tuyến
∆2: mx + y + 1 = 0 có vectơ pháp tuyến
Do đó
Theo đề, ta có (∆1, ∆2) = 30° nên ta có:
Vậy thỏa mãn yêu cầu bài toán.
Do đó ta chọn phương án A.
Câu 11:
Cho ∆ABC có A(2; 3), B(–4; 5), C(6; –5). Gọi M, N lần lượt là trung điểm của AB và AC. Phương trình tham số của đường thẳng MN là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
• Điểm M là trung điểm AB với A(2; 3) và B(–4; 5)
Suy ra
Khi đó ta có M(–1; 4).
• Điểm N là trung điểm AC với A(2; 3) và C(6; –5).
Suy ra
Khi đó ta có N(4; –1).
• Với M(–1; 4) và N(4; –1) ta có:
Đường thẳng MN đi qua điểm M(–1; 4), có vectơ chỉ phương
Suy ra phương trình tham số của đường thẳng MN là
Do đó phương án A đúng.
• Ở phương án B, C, ta có vectơ chỉ phương .
1.5 – (–1).5 = 10 ≠ 0.
Do đó không cùng phương với vectơ chỉ phương của đường thẳng MN.
Vì vậy phương án B, C sai.
• Ở phương án D, ta có vectơ chỉ phương
Với và ta có:
1.1 – (–1).1 = 2 ≠ 0.
Do đó không cùng phương với vectơ chỉ phương của đường thẳng MN.
Vì vậy phương án D sai.
Vậy ta chọn phương án A.
Câu 12:
Cho (d): x= 2+3t; y = 3+t . Hỏi có bao nhiêu điểm M ∈ (d) cách A(9; 1) một đoạn bằng 5?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có M ∈ (d).
Suy ra tọa độ M(2 + 3t; 3 + t).
Với A(9; 1) và M(2 + 3t; 3 + t) ta có:
Theo đề, ta có AM = 5.
⇔ (3t – 7)2 + (t + 2)2 = 25
⇔ 9t2 – 42t + 49 + t2 + 4t + 4 = 25
⇔ 10t2 – 38t + 28 = 0
⇔ t = 14/5 hoặc t = 1.
Vậy có hai điểm M thỏa mãn yêu cầu bài toán là , M(5; 4).
Do đó ta chọn phương án B.
Câu 13:
Phương trình của đường thẳng (d) song song với (d’): 6x + 8y – 1 = 0 và cách (d’) một đoạn bằng 2 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
(d’) có vectơ pháp tuyến là
Vì (d) // (d’) nên (d) cũng nhận làm vectơ pháp tuyến.
Do đó phương trình (d) có dạng: 6x + 8y + c = 0 (c ≠ –1).
Chọn ∈ (d’).
Vì (d) // (d’) nên khoảng cách giữa (d) và (d’) chính là d(A, (d)).
Do đó d(A, (D)) = 2.
⇔ |c + 1| = 20.
⇔ c + 1 = 20 hoặc c + 1 = –20.
⇔ c = 19 (nhận vì 19 ≠ –1) hoặc c = –21 (nhận vì –21 ≠ –1).
Vậy có hai đường thẳng (d) thỏa mãn yêu cầu bài toán có phương trình là:
6x + 8y + 19 = 0 và 6x + 8y – 21 = 0.
Vậy ta chọn phương án D.
Câu 14:
Cho đường thẳng (d): x – 2y + 5 = 0. Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
• (d): x – 2y + 5 = 0 ⇔ 2y = x + 5 ⇔
Do đó (d) có hệ số góc k=1/2
Vì vậy phương án A đúng.
• (d) và (d’) có vectơ pháp tuyến lần lượt là và
Ta có
Do đó (d) và (d’) song song hoặc trùng nhau.
Vì vậy phương án B sai.
• Thay tọa độ A(1; –2) vào phương trình (d), ta được:
1 – 2.(–2) + 5 = 10 ≠ 0.
Suy ra A(1; –2) không thuộc (d) hay (d) không đi qua A(1; –2).
Do đó phương án C sai.
• (d) có vectơ pháp tuyến
Suy ra (d) có vectơ chỉ phương
Ở phương án D, ta có vectơ chỉ phương
Ta có: 2.(–2) – 1.1 = –5 ≠ 0.
Suy ra không cùng phương với
Do đó phương trình tham số ở đáp án D không phải là phương trình tham số của (d).
Vì vậy phương án D sai.
Vậy ta chọn phương án A.
Câu 15:
Cho ∆ABC có C(–1; 2), đường cao BH: x – y + 2 = 0, đường phân giác trong AN: 2x – y + 5 = 0. Tọa độ điểm A là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
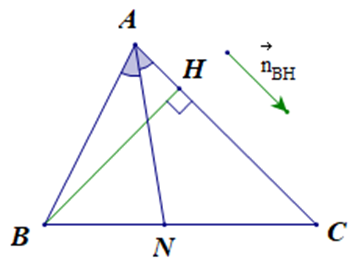
Đường cao BH: x – y + 2 = 0 có vectơ pháp tuyến là
Vì BH là đường cao của ∆ABC nên BH ⊥ AC.
Suy ra vectơ pháp tuyến của BH là vectơ chỉ phương của AC.
Do đó vectơ chỉ phương của AC là
Vì vậy AC có vectơ pháp tuyến là
Đường thẳng AC đi qua C(–1; 2), có vectơ pháp tuyến .
Suy ra phương trình AC: 1(x + 1) + 1(y – 2) = 0.
⇔ x + y – 1 = 0.
Ta có A là giao điểm của AC và AN.
Do đó tọa độ của điểm A là nghiệm của hệ phương trình:
Khi đó ta có
Vậy ta chọn phương án A.
