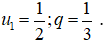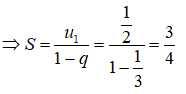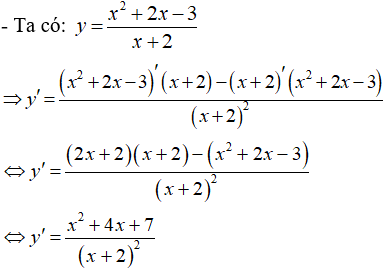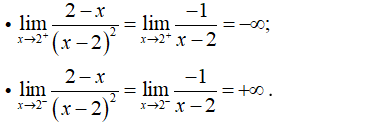Đề thi Học kì 2 Toán 11 có đáp án (Đề 1)
-
266 lượt thi
-
50 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số f(x)liên tục trên đoạn [a ; b] và f(a) = b, f(b) = a, với 0 < a < b. Khi đó phương trình nào trong các phương trình sau đây luôn có nghiệm trên khoảng (a, b).
 Xem đáp án
Xem đáp án
Chọn C.
- Hàm số g(x) = f(x) - x xác định và liên tục trên đoạn [a ; b].
- Suy ra: phương trình f(x) – x = 0 luôn có nghiệm trên khoảng (a, b).
Câu 3:
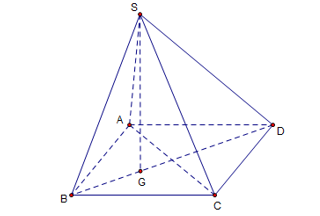
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc . Biết SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng:
 Xem đáp án
Xem đáp án
Chọn D.
- Gọi G là trọng tâm tam giác ABC.
- Hình chóp S.ABC là hình chóp đều nên SG ⊥ (ABC).
→ Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng
Câu 4:
Một cấp số cộng gồm 8 số hạng với số hạng đầu bằng - 15 và số hạng cuối là 69. Tìm công sai của cấp số cộng.
 Xem đáp án
Xem đáp án
Chọn C
- Theo đầu bài ta có:
- Ta có:
Câu 5:
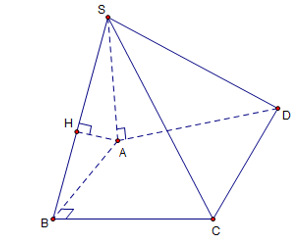
Cho hình chóp S.ABCD có SA⊥(ABC) và tam giác ABC vuông ở B. Gọi AH là đường cao của tam giác SAB. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Chọn B.
+) Vì tam giác ABC vuông tại B nên BC ⊥ AB.
- Lại có:
+) Theo gt AH ⊥ SB vậy:
- Do đó AH không thể vuông góc với AC.(Một tam giác không thể có đồng thời hai góc vuông)
Câu 7:
Biết . Tìm tích của a.b
 Xem đáp án
Xem đáp án
Chọn A.
- Ta có:
- Nên x = -1 là 1 nghiệm của
⇒ 1 - a + b = 0.
| HOOCNE | 1 | a | b |
| -1 | 1 | a - 1 | 1 - a + b |
Câu 8:
Cho hàm số . Với giá trị nào của tham số m thì hàm số đã cho liên tục tại điểm ?
 Xem đáp án
Xem đáp án
Chọn A.
- Ta có: f(2) = m.
→ Hàm số liên tục tại điểm x = 2.
Câu 9:
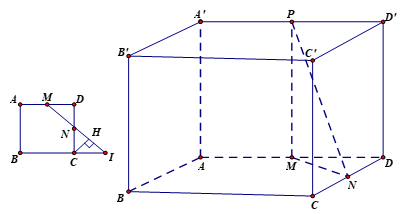
Cho lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a. Gọi M, N, P là trung điểm của các cạnh AD, DC, A’D’. Tính khoảng cách giữa CC’ và mặt phẳng (MNP)?
 Xem đáp án
Xem đáp án
Chọn A.
- Ta có:
Câu 10:
Một người muốn thuê khoan một giếng sâu 20m lấy nước tưới cho vườn cây của gia đình. Tìm hiểu tiền công khoan giếng ở một cơ sở nọ, họ tính theo cách sau đây: giá của mét khoan đầu tiên là 10.000 đồng và kể từ mét khoan thứ hai trở đi, giá của mỗi mét sau tăng lên 7% giá của mét khoan ngay trước nó. Hỏi người ấy cần phải trả số tiền bao nhiêu cho cơ sở khoan giếng?
 Xem đáp án
Xem đáp án
Chọn C.
- Ta có:
Câu 11:
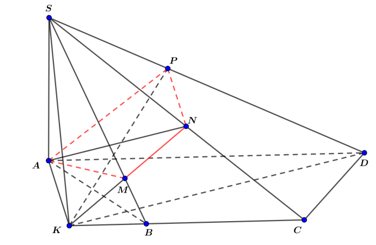
Cho hình chóp S.ABCD có SA ⊥ (ABCD), tứ giác ABCD là hình thang cân có đáy lớn AD gấp đôi đáy nhỏ BC và cạnh bên AB = BC. Mặt phẳng (P) đi qua A, vuông góc với SD và cắt SB, SC, SD lần lượt tại M, N, P. Khi đó ta có thể kết luận gì về tứ giác AMNP?
 Xem đáp án
Xem đáp án
Chọn A.
- Dựng AP ⊥ SD (P ∈ SD).
- Trong mp(SCD) dựng PN ⊥ SD (N ∈ SC)
- Khi đó mặt phẳng (P) ≡ (APN).
- Trong mặt phẳng (ABCD) dựng AK ⊥ AD (K ∈ BC).
- Mà: AK ⊥ SA ⇒ AK ⊥ SD ⇒ K ∈ (APN).
- Trong (SBC) , gọi M = NK ∩ SB. Khi đó tứ giác AMNP là thiết diện của mặt phẳng (P) với hình chóp S.ABCD suy ra tứ giác AMNP nội tiếp đường tròn.
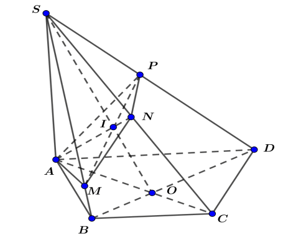
Cách khác:
- Dựng AP ⊥ SD (P ∈ SD).
- Trong (SCD) dựng PN ⊥ SD (N ∈ SC).
- Khi đó mặt phẳng (P) ≡ (APN).
- Trong (ABCD), gọi O = AC ∩ BD.
- Trong (SAC), gọi I = AC ∩ SO.
- Trong (SBD), gọi M = PI ∩ SB.
- Khi đó mặt phẳng (P) ≡ (AMNP).
- Ta có: IA.IN = IP.IM ⇒ AMNP nội tiếp đường tròn.
Câu 12:
Cho cấp số cộng có tổng của n số hạng đầu tiên được tính bởi công thức 2. Gọi M là tổng của số hạng đầu tiên và công sai của cấp số cộng. Khi đó:
 Xem đáp án
Xem đáp án
Chọn B.
- Ta có:
- Vậy
Câu 13:
Trong các giới hạn sau, giới hạn nào không tồn tại.
 Xem đáp án
Xem đáp án
Chọn B.
- Xét phương án B, ta có:
- Suy ra:
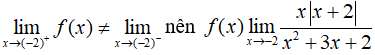
Câu 14:
Gọi S là tập các số nguyên của a sao cho có giá trị hữu hạn. Tính tổng các phần tử của S.
 Xem đáp án
Xem đáp án
Chọn C.
- Ta có:
- Vì:
- Suy ra: 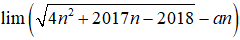
Câu 15:
Cho hàm số . Tìm khẳng định sai trong các khẳng định sau
 Xem đáp án
Xem đáp án
- Ta có:
- Suy ra:
nên hàm số gián đoạn tại điểm
Chọn D
Câu 16:
Cho chuyển động thẳng xác định bởi phương trình ( t tính bằng giây; s tính bằng mét). Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn A.
- Ta có, phương trình vận tốc của chuyển động là:
- Do đó v(4) = 15 (m/s).
Câu 18:
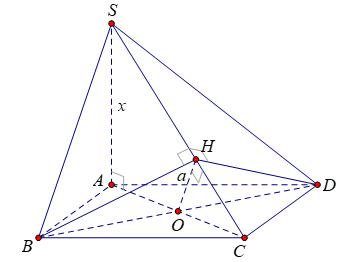
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA ⊥ (ABCD), SA = x. Tìm x để hai mặt phẳng (SBC) và (SCD) tạo với nhau một góc .
 Xem đáp án
Xem đáp án
Chọn D.
- Kẻ BH ⊥ SC ⇒ DH ⊥ SC (hai đường cao tương ứng của hai tam giác bằng nhau).
- Có 2 trường hợp xảy ra:
TH1:
- Xét hai tam giác đồng dạng SAC và OHC ta có
TH2:
- Xét hai tam giác đồng dạng SAC và OHC ta có:
Câu 19:
Giới hạn (nếu tồn tại và hữu hạn) nào sau đây dùng để định nghĩa đạo hàm của hàm số y = f(x) tại điểm ?
 Xem đáp án
Xem đáp án
Chọn C.
- Theo định nghĩa đạo hàm tại điểm
Câu 20:
Tìm khẳng định đúng trong các định đúng trong các khẳng định sau đây.
 Xem đáp án
Xem đáp án
Chọn B.
- Theo tính chất giới hạn của hàm số.
Câu 21:
Cho cấp số cộng (un) có số hạng đầu là u1 = 1 và công sai d = 1. Tìm n sao cho tổng của n số hạng đầu tiên của cấp số cộng đó bằng 3003.
 Xem đáp án
Xem đáp án
Chọn C
- Do công sai và số hạng đầu là d = 1, nên đây là tổng của n số tự nhiên đầu tiên là:
Câu 22:
Tìm khẳng định đúng trong các khẳng định sau đây.
 Xem đáp án
Xem đáp án
Chọn B
- Một hàm số có giới hạn tại điểm x = a thì nó liên tục tại x = a nhưng liên tục thì chưa chắc có đạo hàm ví dụ như hàm số:
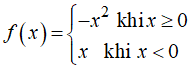
Câu 23:
Viết phương trình tiếp tuyến của đồ thị hàm số sao cho tiếp tuyến có hệ số góc nhỏ nhất.
 Xem đáp án
Xem đáp án
Chọn C
- Ta có:
- Hệ số góc của tiếp tuyến đồ thị hàm số là một giá trị của y’, nên hệ số góc nhỏ nhất là k = -6, ứng với hoành độ tiếp điểm là x = -1 ⇒ y = 5.
→ Phương trình tiếp tuyến là:
y = -6(x + 1) + 5, hay y = -6x - 1.
Câu 24:
Một cấp số nhân có bảy số hạng với số hạng đầu và công bội là các số âm. Biết tích của số hạng thứ ba và số hạng thứ năm bằng 5184; tích của số hạng thứ năm và số hạng cuối bằng 746496. Khi đó số hạng thứ năm là:
 Xem đáp án
Xem đáp án
Chọn D
- Gọi là cấp số nhân cần tìm và q là công bội của cấp số nhân đó.
- Giả thiết ta có:
Câu 25:
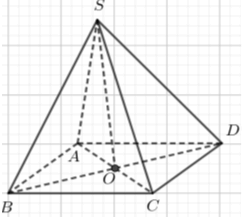
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trong các đẳng thức véc tơ sau đây, đẳng thức nào đúng?
 Xem đáp án
Xem đáp án
Chọn D.
- Gọi O = AC ∩ BD ⇒ O là trung điểm của AC và BD.
Câu 26:
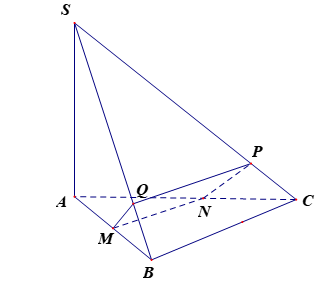
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA vuông góc với đáy. Mặt phẳng (P) đi qua trung điểm M của AB và vuông góc với SB, cắt AC, SC, SB lần lượt tại N, P, Q. Tứ giác M PQ là hình gì?
 Xem đáp án
Xem đáp án
Chọn A.
- Trong (SAB), từ M kẻ đường thẳng vuông góc với SB tại Q.
- Trong (SBC) từ Q kẻ đường thẳng vuông góc với SB cắt SC tại P.
- Do đó BC// QP, trong (ABC) từ M kẻ đường thẳng song song với BC cắt AC tại N.
- Xét tứ giác MNPQ, ta có BC // QP nên tứ giác là là hình thang.
- Mặt khác:
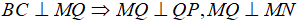
nên tứ giác MNPQ là hình thang vuông.
Câu 27:
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Trong ba câu trên:
 Xem đáp án
Xem đáp án
+) (1) Nếu hàm số f(x) có đạo hàm tại điểm Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm thì f(x) có đạo hàm tại điểm đó.
- Trong ba câu trên: thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
+) (2) Nếu hàm số f(x) liên tục tại điểm thì f(x) có đạo hàm tại điểm đó.Đây là mệnh đề sai.
Phản ví dụ:
- Lấy hàm f(x) = |x| ta có D = R nên hàm số f(x) liên tục trên R
- Nhưng ta có
- Nên hàm số không có đạo hàm tại x = 0.
- Vậy mệnh đề (2) là mệnh đề sai.
+) (3) Nếu f(x) gián đoạn tại thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại thì f(x) không có đạo hàm tại điểm đó.
- Vậy (3) là mệnh đề đúng.
Chọn A.
Câu 28:
Cho dãy số xác định bởi và . Số hạng tổng quát của dãy số này là:
 Xem đáp án
Xem đáp án
Chọn B.
- Ta có, và nên dãy số là cấp số cộng với công sai d = 3, số hạng đầu .
- Do đó số hạng tổng quát của dãy số này là:
Câu 30:
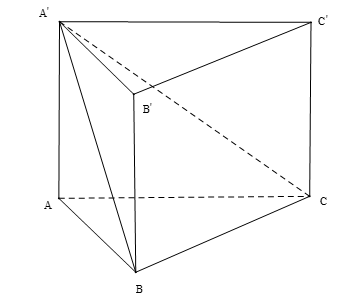
Cho hình lăng trụ đứng tam giác ABC. A’B’C’, có cạnh bên AA’ = 21 cm, tam giác ABC vuông cân tại A, BC = 42 cm. Tính khoảng cách từ A đến mặt phẳng (A’BC).
 Xem đáp án
Xem đáp án
Chọn B.
- Tam giác ABC vuông cân tại A, BC = 42cm
- Tứ diện A.A’BC là tứ diện vuông tại A. Gọi h = d( A, (A’BC)), ta có:
Câu 31:
Trong các mệnh đề sau mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Chọn C.
- Phương án A sai vì góc giữa hai đường thẳng có thể là góc vuông.
- Phương án B sai vì đường thẳng b có thể trùng với đường thẳng c.
- Phương án D sai vì góc giữa hai vectơ có thể là góc tù.
- Phương án C đúng (theo định nghĩa sách giáo khoa).
Câu 32:
Cho biết tổng . Tìm điều kiện của x để
 Xem đáp án
Xem đáp án
Chọn A.
- Ta có, S là tổng của n số hạng của một cấp số nhân với
- Suy ra 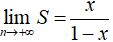
- Do đó |q| < 1 hay |x| < 1.
Câu 33:
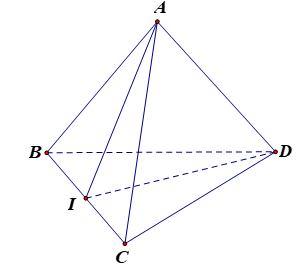
Cho tứ diện ABCD, biết hai tam giác ABC và BCD là hai tam giác cân có chung cạnh đáy BC. Gọi I là trung điểm của cạnh BC. Khẳng định nào đúng trong các khẳng định sau?
 Xem đáp án
Xem đáp án
Chọn A.
+) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao: AI ⊥ BC (1)
+) Tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao: DI ⊥ BC (2)
- Từ (1) và (2) suy ra BC ⊥ (ADI).
Câu 34:
Tìm mệnh đề sai trong các mệnh đề sau đây.
 Xem đáp án
Xem đáp án
Chọn D.
- Ta có khoảng cách giữa hai đường thẳng chéo nhau a và b là khoảng cách từ một điểm N bất kỳ trên b đến mặt phẳng (P) chứa a và song song với b.
Câu 38:
Trong các dãy số sau, dãy số nào là một cấp số nhân.
 Xem đáp án
Xem đáp án
Chọn B.
- Theo tính chất của cấp số nhân:
+ Đáp án A: nên A sai.
+ Đáp án C: nên C sai.
+ Đáp án D: 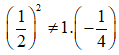
Câu 40:
Cho hàm số f(x). Tìm khẳng định đúng trong các khẳng định sau đây.
 Xem đáp án
Xem đáp án
Chọn D.
- Theo lý thuyết.
Câu 41:
Cho hàm số . Tập nghiệm của bất phương trình f'(x) ≤ 0 là:
 Xem đáp án
Xem đáp án
Chọn A
- Ta có:
- Suy ra bất phương trình vô nghiệm.
Câu 43:
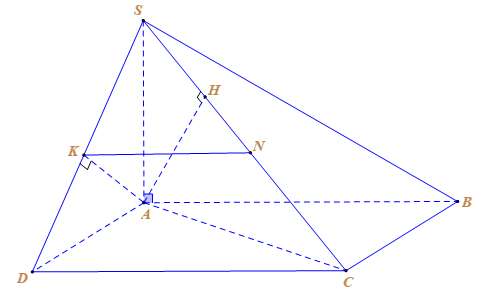
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh bên SA vuông góc với mặt đáy. Gọi H,K lần lượt là hình chiếu của A lên SC; SD. Dựng KN // CD, với N ∈ SC. Trong các mệnh đề sau, mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Chọn B
- Ta có:
Câu 45:
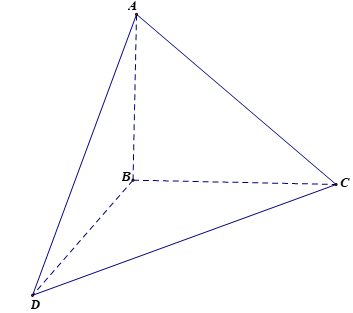
Cho tứ diện ABCD có các cạnh AB, BC, BD vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Chọn A
- Ta có:
- Suy ra AB là hình chiếu của AC lên (ABD).
- Do đó:
Câu 46:
Các giá trị của x để là ba số hạng liên tiếp của một cấp số cộng.
 Xem đáp án
Xem đáp án
Chọn A.
- Để: là ba số hạng liên tiếp của một cấp số cộng thì:
- Biểu diễn 3 họ nghiệm đó trên đường tròn lượng giác thì vị trí các điểm xuất hiện là: 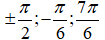
- Đáp án D. Thiếu nghiệm.
- Đáp án A. Đầy đủ nhất.
+) Với 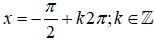
+) Với 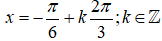
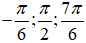
Câu 49:
Tìm mệnh đề đúng trong các mệnh đề sau:
 Xem đáp án
Xem đáp án
Chọn B.
+) Đáp án A. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này mà vuông góc với giao tuyến sẽ vuông góc với mặt phẳng kia.
+) Đáp án C. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng vuông góc với mặt phẳng này sẽ thuộc hoặc không thuộc mặt phẳng kia.
Câu 50:
Cho hàm số . Tìm khẳng định sai trong các khẳng định sau đây?
 Xem đáp án
Xem đáp án
Chọn A.
- Với mọi x ≠ 2 thì hàm số liên tục.
- Tại điểm x = 2 ta có f(2) = 3.
→ Do đó hàm số gián đoạn tại x = 2.

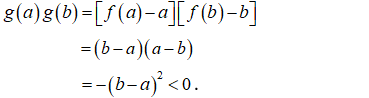
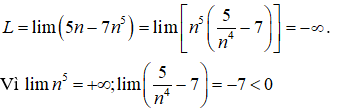
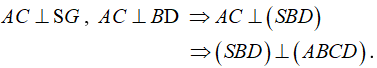
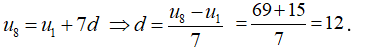
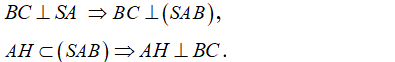
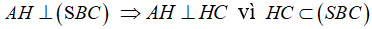
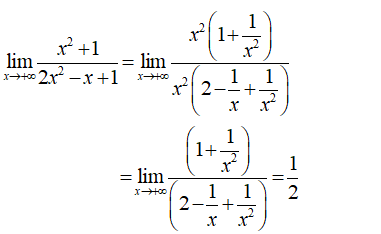
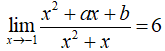
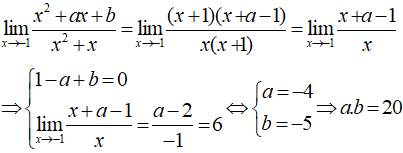
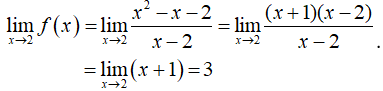
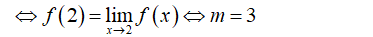
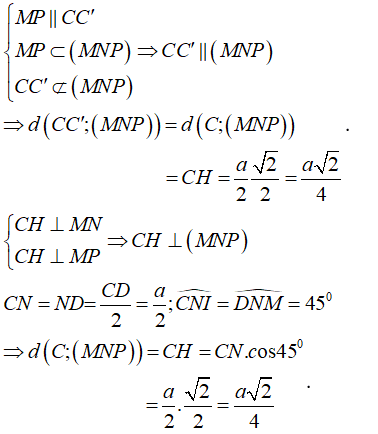
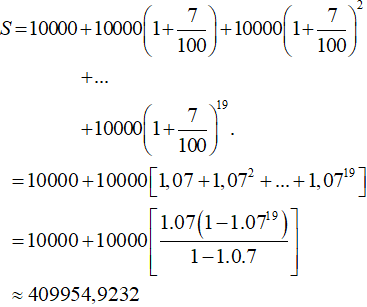
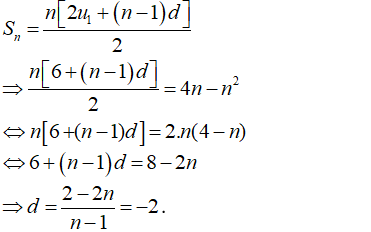

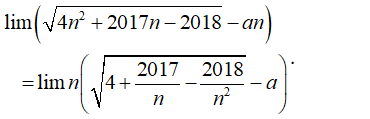
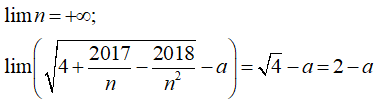
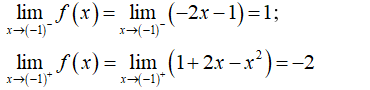
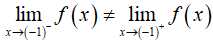
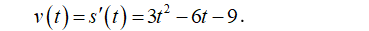
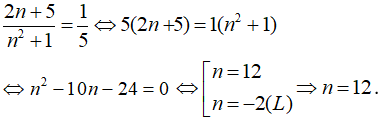
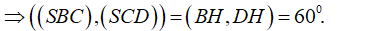
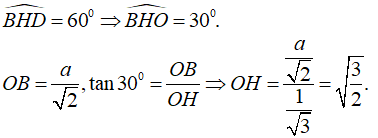
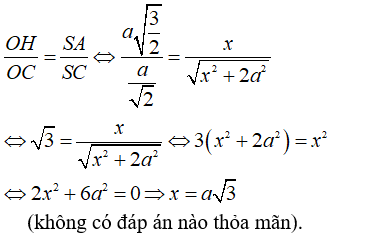
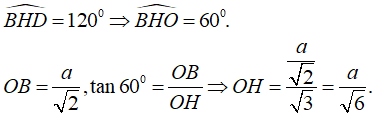
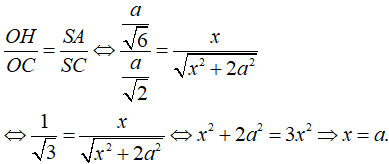
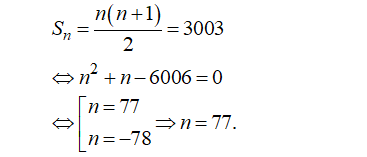
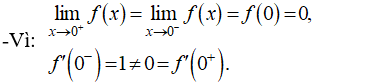
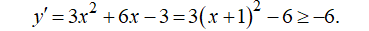
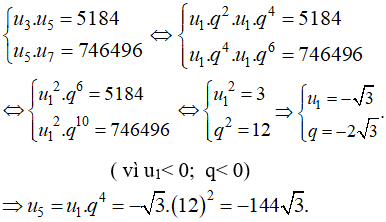
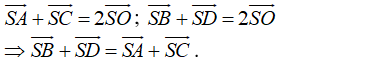
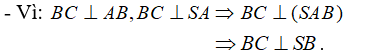
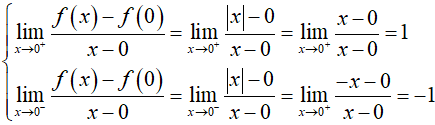
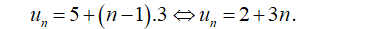
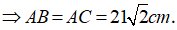
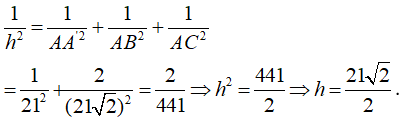
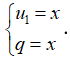
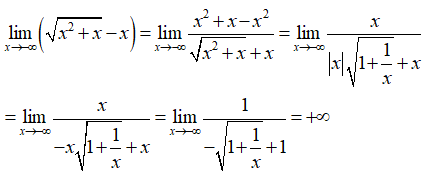
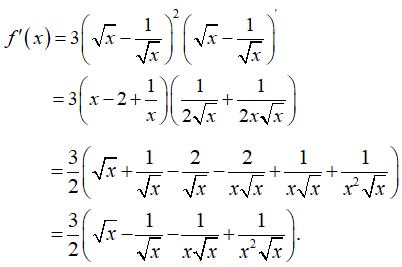
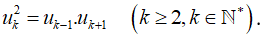
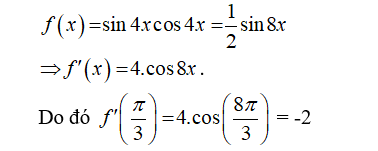
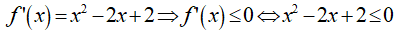
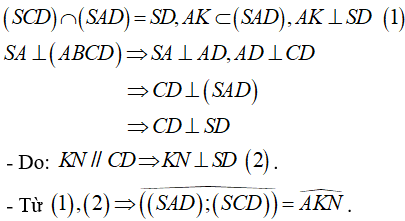
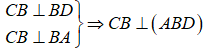
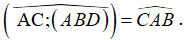
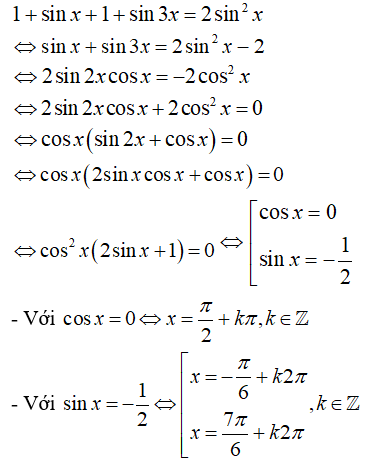
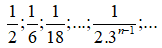 là cấp số nhân lùi vô hạn có:
là cấp số nhân lùi vô hạn có: