Câu hỏi:
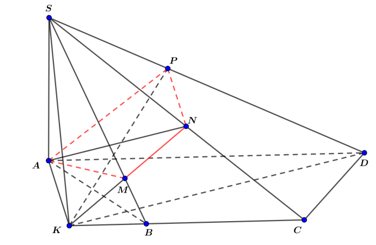
03/04/2024 50Cho hình chóp S.ABCD có SA ⊥ (ABCD), tứ giác ABCD là hình thang cân có đáy lớn AD gấp đôi đáy nhỏ BC và cạnh bên AB = BC. Mặt phẳng (P) đi qua A, vuông góc với SD và cắt SB, SC, SD lần lượt tại M, N, P. Khi đó ta có thể kết luận gì về tứ giác AMNP?
A. AMNP là một tứ giác nội tiếp (không có cặp cạnh đối nào song song).
B. AMNP là một hình thang vuông.
C. AMNP là một hình thang.
D. AMNP là một hình chữ nhật.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A.
- Dựng AP ⊥ SD (P ∈ SD).
- Trong mp(SCD) dựng PN ⊥ SD (N ∈ SC)
- Khi đó mặt phẳng (P) ≡ (APN).
- Trong mặt phẳng (ABCD) dựng AK ⊥ AD (K ∈ BC).
- Mà: AK ⊥ SA ⇒ AK ⊥ SD ⇒ K ∈ (APN).
- Trong (SBC) , gọi M = NK ∩ SB. Khi đó tứ giác AMNP là thiết diện của mặt phẳng (P) với hình chóp S.ABCD suy ra tứ giác AMNP nội tiếp đường tròn.
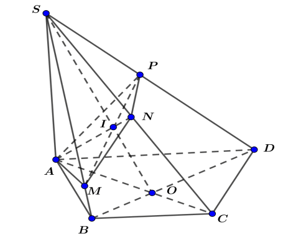
Cách khác:
- Dựng AP ⊥ SD (P ∈ SD).
- Trong (SCD) dựng PN ⊥ SD (N ∈ SC).
- Khi đó mặt phẳng (P) ≡ (APN).
- Trong (ABCD), gọi O = AC ∩ BD.
- Trong (SAC), gọi I = AC ∩ SO.
- Trong (SBD), gọi M = PI ∩ SB.
- Khi đó mặt phẳng (P) ≡ (AMNP).
- Ta có: IA.IN = IP.IM ⇒ AMNP nội tiếp đường tròn.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại thì chắc chắn f(x) không có đạo hàm tại điểm đó.
- Trong ba câu trên:
Câu 2:
Cho tứ diện ABCD, biết hai tam giác ABC và BCD là hai tam giác cân có chung cạnh đáy BC. Gọi I là trung điểm của cạnh BC. Khẳng định nào đúng trong các khẳng định sau?
Câu 5:
Viết phương trình tiếp tuyến của đồ thị hàm số sao cho tiếp tuyến có hệ số góc nhỏ nhất.
Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc . Biết SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng:
Câu 10:
Cho hình chóp S.ABCD có SA⊥(ABC) và tam giác ABC vuông ở B. Gọi AH là đường cao của tam giác SAB. Khẳng định nào sau đây sai?
Câu 13:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trong các đẳng thức véc tơ sau đây, đẳng thức nào đúng?
Câu 15:
Giới hạn (nếu tồn tại và hữu hạn) nào sau đây dùng để định nghĩa đạo hàm của hàm số y = f(x) tại điểm ?