Đề thi giữa kì 1 Toán 7 CTST có đáp án - Đề 2
-
192 lượt thi
-
24 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Trong các câu sau, câu nào đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Số hữu tỉ âm nhỏ hơn số hữu tỉ dương. Đúng.
Số 0 là số hữu tỉ dương. Sai vì số hữu tỉ 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.
Số nguyên âm không phải là số hữu tỉ âm. Sai vì mỗi số nguyên là một số hữu tỉ.
Tập hợp ℚ gồm các số hữu tỉ dương và các số hữu tỉ âm. Sai vì tập hợp ℚ gồm các số hữu tỉ dương, số 0 và các số hữu tỉ âm.
Câu 3:
Cho a = và b = .
Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có:
(quy đồng mẫu số)
Vì ‒2 > ‒3 nên
Hay > .
Vậy > .
Câu 4:
Cho các điểm A, B, C, D biểu diễn các số trên trục số như sau:
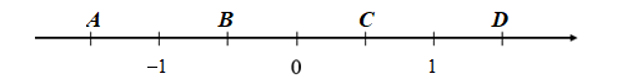
Điểm biểu diễn số là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
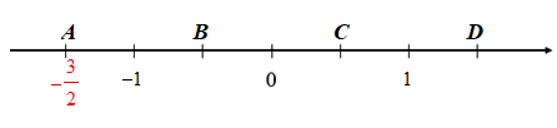
Ta thấy đoạn thẳng đơn vị (chẳng hạn từ 0 đến 1) được chia thành 2 phần bằng nhau, ta lấy một đoạn làm đơn vị mới, đơn vị mới bằng ![]() đơn vị cũ.
đơn vị cũ.
Số hữu tỉ được biểu diễn bởi điểm nằm bên trái điểm 0 và cách 0 một đoạn bằng 3 đơn vị mới (hình vẽ trên). Điểm này chính là điểm A.
Câu 5:
Cho biểu thức . Chọn khẳng định đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau.
Vì các phép tính cộng, nhân, chia ở ngoài ngoặc và phép tính trừ ở trong ngoặc, nên ta thực hiện phép tính trừ trước.
Vậy ta chọn phương án A.
Câu 7:
Trong hình dưới đây có bao nhiêu hình lập phương, bao nhiêu hình hộp chữ nhật?

 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Quan sát hình ta thấy không có hộp quà có dạng hình lập phương, có 4 hộp quà có dạng hình hộp chữ nhật đó là: hộp quà màu hồng nhạt, hộp quà màu xanh lam, hộp quà màu đỏ, hộp quà màu xanh lá cây.
Vậy chọn phương án D.
Câu 8:
Hãy chọn khẳng định sai.
Hình lập phương ABCD.A'B'C'D' có:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hình hộp chữ nhật này có 12 cạnh: AB; BC; CD; DA; A'B'; C'D'; B'C'; D'A'; AA'; BB'; CC'; DD'.
Do đó phương án C là khẳng định sai.
Vậy ta chọn phương án C.
Câu 9:
Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm, AE = 4 cm. Khẳng định đúng là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
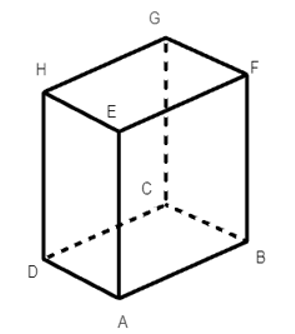
Từ hình hộp chữ nhật ABCD.EFGH ta có các mặt của hình hộp này đều là hình chữ nhật.
Khi đó ta có:
HG = DC = AB = 4 cm;
HE = DA = BC = 2 cm;
GC = HD = AE = 4 cm.
Vậy HG = 4 cm, HE = 2 cm, GC = 4 cm.
Ta chọn đáp án A.
Câu 10:
Chọn khẳng định đúng trong các khẳng định sau:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
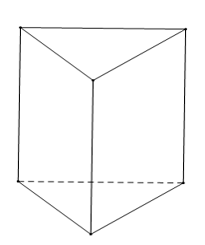
Hình lăng trụ đứng tam giác có hai mặt đáy là hình tam giác nên C đúng.
Câu 11:
Tấm bìa bên dưới có thể tạo lập thành một hình lăng trụ đứng có đáy là tam giác đều.
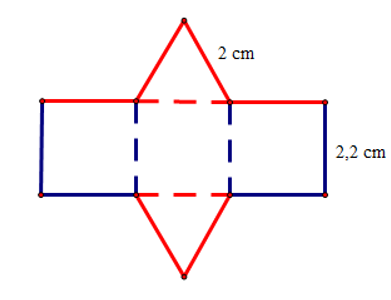
Chiều cao của hình lăng trụ đứng là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Hình lăng trụ đứng có tất cả 5 mặt nên đây là hình lăng trụ đứng tam giác.
Hình lăng trụ đứng tam giác có tất cả 6 đỉnh.
Câu 12:
Chọn phát biểu sai:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Hai góc đối đỉnh là hai góc bằng nhau nên A đúng.
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia nên B đúng.
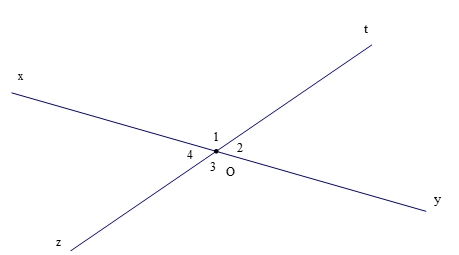
Hai đường thẳng xy và zt cắt nhau tại O (như hình vẽ trên). Ta có và ; và là hai cặp góc đối đỉnh. Do đó hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh nên C đúng.
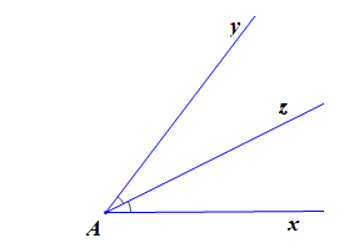
Quan sát hình vẽ trên có: mà hai góc này ở vị trí kề nhau.
Do đó hai góc bằng nhau chưa chắc là hai góc ở vị trí đối đỉnh nên D sai.
Vậy ta chọn phương án D.
Câu 17:
b)
 Xem đáp án
Xem đáp án
b)
–0,4 . (2x + 0,5) = –10
2x + 0,5 = (–10) : (–0,4)
2x + 0,5 = 25
2x = 25 – 0,5
2x = 24,5
x = 24,5 : 2
x = 12,25.
Vậy x = 12,25.
Câu 18:
c) (x – 5)2 = (1 – 3x)2.
 Xem đáp án
Xem đáp án
c) (x – 5)2 = (1 – 3x)2.
Trường hợp 1: x – 5 = 1 – 3x.
x + 3x = 1 + 5.
4x = 6.
.
.
Trường hợp 2: x – 5 = ‒(1 – 3x)
x – 5 = ‒1 + 3x
x ‒ 3x = ‒1 + 5.
‒2x = 4.
x = 4 : (‒2).
x = ‒2.
Vậy ; x = ‒2.
Câu 19:
Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và một cửa sổ hình vuông với các kích thước như hình vẽ.
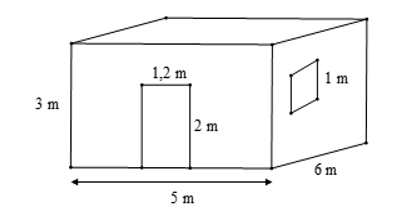
Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này (không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.
 Xem đáp án
Xem đáp án
Để tính được số tiền bác Long dùng để sơn căn phòng ta phải tính được diện tích phần cần sơn.
Diện tích phần cần sơn = Diện tích xung quanh của căn phòng – Diện tích các cửa.
Diện tích xung quanh của căn phòng là:
Sxq = 2. (5 + 6) . 3 = 66 (m2).
Diện tích phần cửa lớn và cửa sổ là:
1,2 . 2 + 1 . 1 = 3,4 (m2)
Diện tích phần cần sơn là:
66 – 3,4 = 62,6 (m2).
Tổng chi phí cần để sơn là:
62,6. 30 000 = 1 878 000 (đồng).
Vậy bác Long cần 1 878 000 đồng để sơn bốn bức tường xung quanh của căn phòng này.
Câu 20:
Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thước thước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m. Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ).
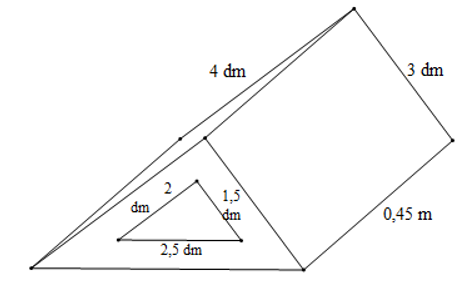
a) Tính thể tích của khối gỗ.
 Xem đáp án
Xem đáp án
Đổi 3 dm = 30 cm; 4 dm = 40 cm; 5 dm = 50 cm;
1,5 dm = 15 cm; 2 dm = 20 cm; 2,5 dm = 25 cm;
0,45 m = 45 cm.
a) Thể tích của khối gỗ là:
. 40 . 30 . 45 –. 20 . 15 . 25 = 23 250 (cm3).
Câu 21:
b) Người ta muốn sơn tất cả các bề mặt của khối gỗ. Tính diện tích cần sơn (đơn vị mét vuông).
 Xem đáp án
Xem đáp án
b) Diện tích xung quanh của khối kim loại là:
(30 + 40 + 50).45 = 5 400 (cm2).
Diện tích xung quanh của cái lỗ là:
(20 + 15 + 25).45 = 2 700 (cm2).
Diện tích hai đáy trừ đi diện tích hai cái đáy lỗ là:
.30.40 – .15.20 = 450 (cm2).
Diện tích bề mặt cần sơn là:
5 400 + 2 700 – 450 = 7 650 (cm2) = 0,765 (m2)
Vậy diện tích cần sơn là 0,765 mét vuông.
Câu 22:
Cho hình vẽ dưới đây:
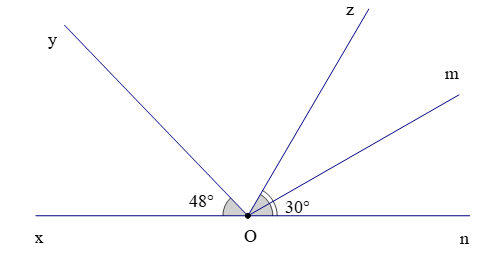
Biết rằng , và Om là tia phân giác của .
a) Kể tên các góc (khác góc bẹt) kề với góc zOm; góc kề bù với góc mOn.
 Xem đáp án
Xem đáp án
a) Các góc (khác góc bẹt) kề với góc zOm là: góc zOy, góc zOx, góc mOn.
Góc kề bù với góc mOn là: góc mOx.
Câu 23:
b) Tính số đo của góc yOz.
 Xem đáp án
Xem đáp án
b) Theo bài ta có Om là tia phân giác của
Suy ra (tính chất tia phân giác của một góc) (1)
Mà (hai góc kề nhau) (2)
Từ (1) và (2) suy ra
Suy ra
Ta có (hai góc kề nhau) và (hai góc kề bù)
Suy ra
Hay
Suy ra
Vậy số đo của góc yOz là 72°.
Câu 24:
Một công ty phát triển kĩ thuật có một số thông báo rất hấp dẫn: Cần thuê một nhóm kĩ thuật viên hoàn thành một dự án trong vòng 17 ngày, công việc rất khó khăn nhưng tiền công cho dự án rất thú vị. Nhóm kĩ thuật viên được nhận làm dự án sẽ lựa chọn một trong hai phương án trả tiền công như sau:
– Phương án 1: Nhận một lần và nhận tiền công trước với mức tiền 170 triệu đồng;
– Phương án 2: Ngày đầu tiên nhận 3 đồng, ngày sau nhận gấp 3 lần ngày trước đó.
Em hãy giúp nhóm kỹ thuật viên lựa chọn phương án để nhận được nhiều tiền công hơn và giải thích tại sao chọn phương án đó.
 Xem đáp án
Xem đáp án
Theo phương án 2 ta có: Số tiền nhận được vào ngày thứ nhất là 3 đồng; ngày thứ hai là 3 . 3 = 32 đồng; ngày thứ ba là 32 . 3 = 33 đồng; … ; ngày thứ mười bảy là 317 đồng.
Như vậy số tiền công nhận được theo phương án 2 là:
T = 3 + 32 + 33 + … + 317
Suy ra 3T = 3 . (3 + 32 + 33 + … + 317)
= 3. 3 + 3. 32 + 3 . 33 + … + 3 . 317
= 32 + 33 + 34 + … + 318
Do đó 3T – T = (32 + 33 + 34 + … + 318) – (3 + 32 + 33 + … + 317)
Hay 2T = 318 – 3 = 387 420 489 – 3 = 387 420 486 (đồng)
Suy ra T = 193 710 243 (đồng) > 170 000 000 (đồng).
Vậy nhóm kĩ thuật viên nên chọn phương án 2 để nhận được nhiều tiền công hơn.
