30 câu hỏi trắc nghiệm thuộc Đề kiểm tra học kì 1 Chuyên đề toán 11: Kiểm tra cuối kì có đáp án (Đề 4)

Câu 1:

Trong không gian cho đường thẳng $Δ$ và điểm O. Qua O có mấy đường thẳng vuông góc với $Δ$ cho trước?

A. Vô số.

B. 2.

C. 3.

D. 1.

Xem đáp án

Chọn A

Câu 2:

Giới hạn nào dưới đây có kết quả bằng 3?

A. $\lim_{x \to 1} \frac{- 3 x}{x - 2}$

B. $\lim_{x \to 1} \frac{3}{x - 2}$

C. $\lim_{x \to 1} \frac{- 3 x}{2 - x}$

D. $\lim_{x \to 1} \frac{3 x}{x - 2}$

Xem đáp án

Chọn A

Câu 3:

Cho a, b, c là các đường thẳng. Mệnh đề nào sau đây đúng?

A. Cho

a / / b

. Mọi mặt phẳng

(α)

chứa c trong đó

c ⊥ a

và

c ⊥ b

thì đều vuông góc với mặt phẳng

(a, b)

.

B. Cho $a ⊥ b$ . Mọi mặt phẳng chứa b đều vuông góc với a.

C. Nếu $a ⊥ b$ và mặt phẳng $(α)$ chứa a; mặt phẳng $(β)$ chứa b thì $(α) ⊥ (β)$ .

D. Cho $a ⊥ b$ nằm trong mặt phẳng $(α)$ . Mọi mặt phẳng $(β)$ chứa a và vuông góc với b thì $(β) ⊥ (α)$

Xem đáp án

Chọn D

Câu 4:

Giá trị $\lim \frac{n - 2}{3 n + 1}$ bằng

A. –2.

B. 1.

C.

\frac{1}{3}

D.

- \frac{1}{3}

Xem đáp án

Chọn C

Câu 5:

Hai đường thẳng a và b nằm trong mp $(α)$ . Hai đường thẳng a' và b' nằm trong mp $(β)$ . Mệnh đề nào sau đây đúng?

A. Nếu

a / / a^{'}

và

b / / b^{'}

thì

(α) / / (β)

.

B. Nếu $(α) / / (β)$ thì $a / / a^{'}$ và $b / / b^{'}$ .

C. Nếu $a / / b$ và $a^{'} / / b^{'}$ thì $(α) / / (β)$ .

D. Nếu a cắt b, a' cắt b' và

a / / a^{'}

và

b / / b^{'}

thì

(α) / / (β)

.

Xem đáp án

Chọn D

Câu 6:

Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, cạnh bên SA vuông góc với đáy, M là trung điểm BC, J là hình chiếu của A lên BC. Kí hiệu $d (A, (S B C))$ là khoảng cách giữa điểm A và mặt phẳng (SBC). Khẳng định nào sau đây đúng?

A.

d (A, (S B C)) = A K

với K là hình chiếu của A lên SB.

B. $d (A, (S B C)) = A K$ với K là hình chiếu của A lên SJ.

C. $d (A, (S B C)) = A K$ với K là hình chiếu của A lên SC.

D.

d (A, (S B C)) = A K

với K là hình chiếu của A lên SM.

Xem đáp án

Chọn B

Câu 7:

Cho hàm số $f (x) = \sqrt{1 - x^{2}}$ . Khi đó $f^{'} (\frac{1}{2})$ bằng

A. $- \frac{\sqrt{3}}{3}$

B. $\frac{\sqrt{3}}{3}$

C. $- \frac{\sqrt{3}}{2}$

D. $\frac{\sqrt{3}}{2}$

Xem đáp án

Chọn A

Câu 8:

Cho hàm số $y = \frac{2 x + 1}{2 x - 1}$ có đồ thị (C). Hệ số góc của tiếp tuyến với (C) tại điểm có hoành độ bằng 0 là

A. 0.

B. 4.

C. –4.

D. 1.

Xem đáp án

Chọn C

Câu 9:

Trong các mệnh đề sau đây, mệnh đề nào là đúng?

A. Từ

\vec{A B} = - 3 \vec{A C}

ta suy ra

\vec{C B} = \vec{A C}

.

B. Vì $\vec{A B} = - 2 \vec{A C} + 5 \vec{A D}$ nên bốn điểm A, B, C, D cùng thuộc một mặt phẳng.

C. Từ $\vec{A B} = 3 \vec{A C}$ ta suy ra $\vec{B A} = - 3 \vec{C A}$ .

D. Nếu

\vec{A B} = - \frac{1}{2} \vec{B C}

thì B là trung điểm của đoạn AC.

Xem đáp án

Chọn B

Câu 10:

Phương trình tiếp tuyến của đồ thị hàm số $y = x^{4} + 2 x^{2} - 1$ tại tiếp điểm có hoành độ bằng –1 là

A. $y = 8 x + 10$

B. $y = 8 x - 6$

C. $y = - 8 x + 10$

D. $y = - 8 x - 6$

Xem đáp án

Chọn D

Câu 11:

Cho hình lập phương $A B C D . A_{1} B_{1} C_{1} D_{1}$ có cạnh a. Gọi M là trung điểm AD. Giá trị $\vec{B_{1} M} . \vec{B D_{1}}$ bằng

A. $\frac{3}{2} a^{2}$

B. $\frac{1}{2} a^{2}$

C. $a^{2}$

D. $\frac{3}{4} a^{2}$

Xem đáp án

Chọn B

Câu 12:

Cho hàm số $f (x) = \frac{4}{5} x^{5} - 6$ . Số nghiệm của phương trình $f^{'} (x) = 4$ là

A. 0.

B. 1.

C. 2.

D. 3.

Xem đáp án

Chọn C

Câu 13:

Cho hình chóp S.ABCD có $S A ⊥ (A B C D)$ và đáy là hình vuông. Khẳng định nào sau đây đúng?

A. $A C ⊥ (S A D)$

B. $A C ⊥ (S A B)$

C. $A C ⊥ (S B D)$

D. $B C ⊥ (S A B)$

Xem đáp án

Chọn D

Câu 14:

Giá trị $\lim [\sqrt{n} (\sqrt{n + 1} - \sqrt{n - 1})]$ bằng

A. –1.

B. 0.

C. 1.

D.

+ \infty

Xem đáp án

Chọn C

Câu 15:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông và $S A ⊥ (A B C D)$ , gọi O là tâm hình vuông ABCD. Khẳng định nào sau đây sai?

A.

(S A C) ⊥ (S B D)

B. Góc giữa hai mặt phẳng $(S B C)$ và $(A B C D)$ là góc $\hat{A B S}$

C. Góc giữa hai mặt phẳng $(S B D)$ và $(A B C D)$ là góc $\hat{S O A}$

D. Góc giữa hai mặt phẳng

(S A D)

và

(A B C D)

lá góc

\hat{S D A}

.

Xem đáp án

Chọn D

Câu 16:

Giá trị $\lim_{x \to 1} \frac{2 x^{2} + x - 3}{x - 1}$ bằng

A.

+ \infty

B. 5.

C. –2.

D. 1.

Xem đáp án

Chọn B

Câu 17:

Cho hàm số $f (x) = \{\begin{cases} \frac{\sin 5 x}{5 x} x \neq 0 \\ a + 2 x = 0 \end{cases}$ . Giá trị của a để hàm số f(x) liên tục tại x=0 là

A. a=1

B. a=-1

C. a=-2

D. a=2

Xem đáp án

Chọn B

Câu 18:

Cho $f (x) = \sqrt{1 + 3 x} + \sqrt[3]{1 + 2 x}$ , $g (x) = \sin x$ . Giá trị $\frac{f^{'} (0)}{g^{'} (0)}$ bằng

A. $\frac{5}{6}$

B. $- \frac{5}{6}$

C. 0

D. 1

Xem đáp án

Chọn A

Câu 19:

Đạo hàm của hàm số $f (x) = \frac{x^{2} + x + |x + 1|}{x}$ tại $x_{0} = - 1$ bằng

A. 2.

B. 0.

C. 3.

D. không tồn tại đạo hàm tại

Xem đáp án

Chọn D

Câu 20:

Giới hạn $\lim_{x \to 0} \frac{\sqrt{1 + x} - 1}{x}$ bằng

A. đạo hàm tại x=-1 của hàm số

y = \sqrt{x + 1}

B. đạo hàm tại x=0 của hàm số $y = \sqrt{x + 1}$

C. đạo hàm tại x=0 của hàm số $y = \sqrt{x}$

D. đạo hàm tại x=1 của hàm số

y = \sqrt{x + 1}

Xem đáp án

Chọn B

Câu 21:

a) Tính giới hạn $\lim (3^{4} {.2}^{n + 1} - {5.3}^{n})$ .

Xem đáp án

a) Ta có $\{\begin{cases} \lim 3^{n} = + \infty \\ \lim (162. {(\frac{2}{3})}^{n} - 5) = - 5 < 0 \end{cases}$

Suy ra

\lim (3^{4} {.2}^{n + 1} - {5.3}^{n}) = \lim 3^{n} (162. {(\frac{2}{3})}^{n} - 5) = - \infty

Câu 22:

b) Tính giới hạn $A = \lim_{x \to 2} \frac{x^{3} - 8}{x - 2}$

Xem đáp án

b) Ta có

\lim_{x \to 2} \frac{x^{3} - 8}{x - 2} = \lim_{x \to 2} \frac{(x - 2) (x^{2} + 2 x + 4)}{x - 2} = \lim_{x \to 2} (x^{2} + 2 x + 4) = 12

Câu 23:

c) Tính giới hạn $A = \lim_{x \to \infty} (\sqrt{x^{2} + x} - \sqrt[3]{x^{3} - x^{2}})$

Xem đáp án

c) Ta có $\lim_{x \to + \infty} (\sqrt{x^{2} + x} - \sqrt[3]{x^{3} - x^{2}}) = \lim_{x \to + \infty} (\sqrt{x^{2} + x} - x + x - \sqrt[3]{x^{3} - x^{2}})$

= \lim_{x \to + \infty} (\frac{x}{\sqrt{x^{2} + 1} + x} + \frac{x^{2}}{x^{2} + x \sqrt[3]{x^{3} - 1} + \sqrt[3]{{(x^{3} - 1)}^{2}}}) = \frac{1}{2} + \frac{1}{3} = \frac{5}{6}

Câu 24:

a) Cho hàm số $f (x) = \{\begin{cases} \frac{x^{2} + 3 x - 4}{x - 1} khi x > 1 \\ - 2 a x + 1 khi x \leq 1 \end{cases}$

Xác định a để hàm số liên tục tại điểm x=1

Xem đáp án

a) Hàm số liên tục tại điểm x=1 khi $- 2 a .1 + 1 = \lim_{x \to 1^{+}} \frac{(x - 1) (x + 4)}{(x - 2)}$

\Leftrightarrow - 2 a + 1 = \lim_{x \to 1^{+}} (x + 4) \Leftrightarrow - 2 a + 1 = 5 \Leftrightarrow a = - 2

Câu 25:

b) Viết phương trình tiếp tuyến của đường cong $y = x^{3}$ tại điểm có tung độ bằng 8.

Xem đáp án

b) Với $y_{0} = 8 \Rightarrow x_{0} = 2$ . Ta tính được $k = y^{'} (2) = 12$ .

Ta có

\{\begin{cases} x_{0} = 2 \\ y_{0} = 8 \\ k = 12 \end{cases} \Rightarrow

phương trình tiếp tuyến

y - 8 = 12 (x - 2) \Leftrightarrow y = 12 x - 16

.

Câu 26:

c) Cho hàm số $y = - x^{3} + 3 x^{2} - 3$ có đồ thị (C). Viết phương trình tiếp tuyến của (C) vuông góc với đường thẳng $y = \frac{1}{9} x + 2019$

Xem đáp án

c) Phương trình tiếp tuyến có dạng $y = y^{'} (x_{0}) (x - x_{0}) + y_{0}$

Trong đó $y^{'} = - 3 x^{2} + 6 x$

Theo đề ta có $y^{'} (x_{0}) = - 9 \Leftrightarrow - 3 {x_{0}}^{2} + 6 x_{0} = - 9 \Leftrightarrow - 3 {x_{0}}^{2} + 6 x_{0} + 9 = 0$

$\Leftrightarrow [\begin{array}{l} x_{0} = - 1 \Rightarrow y_{0} = 1 \\ x_{0} = 3 \Rightarrow y_{0} = - 3 \end{array}$

Vậy có 2 phương trình tiếp tuyến cần tìm là

y = - 9 x - 8

;

y = - 9 x + 24

Câu 27:

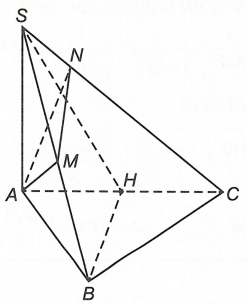
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B, SA vuông góc với đáy, $S A = a \sqrt{2}$ , AB=a, BC=2a.

a) Chứng minh tam giác SBC vuông.

Xem đáp án

a) Ta có $S A ⊥ (A B C) (1) \Rightarrow S A ⊥ B C$

Mà $A B ⊥ B C$ và trong (SAB): $S A \cap A B = A$ nên $B C ⊥ (S A B)$ (2)

. $\Rightarrow B C ⊥ S B$

Vậy tam giác ABC vuông tại B.

Câu 28:

b) Gọi H là chân đường cao vẽ từ B của tam giác ABC. Chứng minh $(S A C) ⊥ (S B H)$ .

Xem đáp án

b) Ta có

$\{\begin{cases} B H ⊥ A C \\ B H ⊥ S A (do (1), B H \subset (A B C)) \\ (S A C) : S A \cap A C = A \end{cases} \Rightarrow B H ⊥ (S A C) \Rightarrow (S B H) ⊥ (S A C)$

Câu 29:

c) Tính khoảng cách từ A đến (SBC)

Xem đáp án

c) Từ $(2) \Rightarrow (S B C) ⊥ (S A B)$

$(S B C) \cap (S A B) = S B$

Trong $(S A B)$ kẻ $A M ⊥ S B$ tại M

$\Rightarrow A M ⊥ (S B C) (3) \Rightarrow$

M là hình chiếu vuông góc của A lên $(S B C)$ .

Do đó $d (A; (S B C)) = A M$

Xét tam giác SAB vuông tại A có AM là đường cao, ta có

$\frac{1}{A M^{2}} = \frac{1}{S A^{2}} + \frac{1}{A B^{2}} \Leftrightarrow \frac{1}{A M^{2}} = \frac{1}{{(a \sqrt{2})}^{2}} + \frac{1}{a^{2}} \Leftrightarrow A M = \frac{a \sqrt{6}}{3}$

Vậy

d (A; (S B C)) = \frac{a \sqrt{6}}{3}

Câu 30:

d) Xác định thiết diện của hình chóp bởi mặt phẳng qua A và vuông góc với SC. Tính diện tích thiết diện đó.

Xem đáp án

d) Trong (SAC): Kẻ $A N ⊥ S C$ tại N.

Mà $A M ⊥ S C$ (do (3)) và trong (AMN): $A M \cap A N = A$ nên $S C ⊥ (A M N)$ .

Suy ra thiết diện của hình chóp bởi mặt phẳng qua A và vuông góc với SC là tam giác AMN.

Ta có $(3) \Rightarrow A M ⊥ M N$ (do $M N \subset (S B C)$ .

Suy ra tam giác AMN vuông tại M.

Xét tam giác ABC vuông tại B, ta có $A C = \sqrt{A B^{2} + B C^{2}} = \sqrt{a^{2} + {(2 a)}^{2}} = a \sqrt{5}$

Xét tam giác SAC vuông tại A có AN là đường cao, ta có $\frac{1}{A N^{2}} = \frac{1}{S A^{2}} + \frac{1}{A C^{2}} \Leftrightarrow \frac{1}{A M^{2}} = \frac{1}{{(a \sqrt{2})}^{2}} + \frac{1}{{(a \sqrt{5})}^{2}} \Leftrightarrow A N^{2} = \frac{10}{7} a^{2}$

Xét tam giác AMN vuông tại M, ta có

$M N = \sqrt{A N^{2} - A M^{2}} = \sqrt{\frac{10}{7} a^{2} - {(\frac{a \sqrt{6}}{3})}^{2}} = \frac{4 a \sqrt{21}}{21}$

Vậy diện tích tam giác AMN là

S_{Δ A M N} = \frac{1}{2} A M . M N = \frac{1}{2} . \frac{a \sqrt{6}}{3} . \frac{4 a \sqrt{21}}{21} = \frac{2 a^{2} \sqrt{14}}{21}

Đề kiểm tra học kì 1 Chuyên đề toán 11: Kiểm tra cuối kì có đáp án

Đề kiểm tra học kì 1 Chuyên đề toán 11: Kiểm tra cuối kì có đáp án (Đề 4)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương