Giải SGK Toán 6 Bài 29 (Kết nối tri thức): Tính toán với số thập phân

Giải SGK Toán 6 Bài 29: Tính toán với số thập phân

Toán lớp 6 trang 31 Bài toán mở đầu: Một tàu thăm dò đáy biển đang ở độ cao – 0,32 km (so với mực nước biển).

Tính độ cao mới của tàu (so với mực nước biển) sau khi tàu nổi lên thêm 0,11 km.

Lời giải: 

Sau khi học bài học ngày hôm nay, các em có thể tính được:

Độ cao mới của tàu là: (– 0,32) + 0,11 = – (0,32 – 0,11) = – 0,21 (km)

Vậy độ cao mới của tàu là – 0,21 km (so với mực nước biển).

Toán lớp 6 trang 31 Hoạt động 1: Tính:

a) 2,259 + 0,31;

b) 11,325 – 0,15.

Lời giải: 

a)

$\begin{array}{l}\text{+}\underset{¯}{\begin{array}{c}\text{ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}2,259}\\ \text{0,31}\end{array}}\\ \text{ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}2,569}\end{array}$                         

Vậy 2,259 + 0,31 = 2, 569

b)

$\begin{array}{l}-\underset{¯}{\begin{array}{c}\text{\hspace{0.17em}\hspace{0.17em}11,325}\\ \text{0,15}\end{array}}\\ \text{ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}11,175}\end{array}$

Vậy 11,325 – 0,15 = 11,175

Toán lớp 6 trang 31 Hoạt động 2: Thực hiện các phép tính sau bằng cách quy về cộng hoặc trừ hai số thập phân dương tương tự như với số nguyên:

a) (–2,5) + (–0,25),

b) (–1,4) + 2,1;

c) 3,2 – 5,7.

Lời giải: 

a) (–2,5) + (–0,25) = – (2,5 + 0,25) = –2,75;

b) (–1,4) + 2,1 = 2, 1 – 1, 4 = 0,7;

c) 3,2 – 5, 7 = –(5,7 – 3,2) = – 2,5.

Giải Toán 6 trang 32 Tập 2

Toán lớp 6 trang 32 Luyện tập 1: Tính:

a) (– 2,259) + 31,3;

b) (– 0,325) – 11,5.

Lời giải: 

a) (–2,259) + 31,3 =  31,3 – 2,259 = 29, 041.

Vậy (– 2,259) + 31,3 = 29, 041.

b) (– 0,325) – 11,5 = – (0,325 + 11,5) = –11,825

Vậy (– 0,325) – 11,5 = –11,825

Toán lớp 6 trang 32 Vận dụng 1:

1. Em hãy giải bài toán mở đầu.    

Một tàu thăm dò đáy biển đang ở độ cao –0,32 km (so với mực nước biển).

Tính độ cao mới của tàu (so với mực nước biển) sau khi tàu nổi lên thêm 0,11 km.

2. Nhiệt độ trung bình năm ở Bắc Cực là –3,4°C, ở Nam Cực là – 49,3°C (Theo www.southpole.aq). Cho biết nhiệt độ trung bình năm ở nơi nào cao hơn và cao hơn bao nhiêu độ C.

Lời giải: 

1. Độ cao mới của tàu sau khi tàu nổi lên thêm 0,11 km là:

 (–0,32) + 0,11 = – (0,32 – 11) = – 0,21 (km)

Vậy độ cao mới của tàu sau khi tàu nổi lên thêm 0,11 km là –0, 21 km

2.

Vì 3,4 < 49,3 nên –3, 4 > –49,3

Do đó nhiệt độ trung bình ở Bắc Cực cao hơn ở Nam Cực và cao hơn số độ C là:

(–3,4) – (– 49,3) = (–3,4) + 49,3 = 49,3 – 3, 4 = 45,9 (độ C)

Vậy nhiệt độ trung bình ở Bắc Cực cao hơn ở Nam Cực và cao hơn.

Toán lớp 6 trang 32 Hoạt động 3: Tính: 12,5. 1,2

Lời giải: 

$\begin{array}{l}\times \underset{¯}{\begin{array}{l}12,5\\ 1,2\end{array}}\\ 250\\ \underset{¯}{125 } \\ 15,00\end{array}$

Vậy 12,5. 1,2 = 15

Toán lớp 6 trang 32 Hoạt động 4: Thực hiện phép nhân sau bằng cách quy về phép nhân hai số thập phân dương tương tự như với số nguyên:

a) (– 12,5). 1,2;

b) (– 12,5). (–1,2).

Lời giải: 

a) (– 12,5). 1,2 = –(12,5. 1,2) = –15

b) (– 12,5). (–1,2) = 12,5. 1,2 = 15

Toán lớp 6 trang 32 Luyện tập 2: Tính:

a) 2,72. (– 3,25);

b) (– 0,827). (–1,1).

Lời giải: 

a) 2,72. (–3,25) = –(2,72. 3,25)

$\begin{array}{l}\times \underset{¯}{\begin{array}{l}2,72\\ 3,25\end{array}}\\ 1360\\ 544\\ 816\\ \overline{8,8400}\end{array}$

$\Rightarrow$ 2,72. (–3,25) = –(2,72. 3,25) = – 8,84.

Vậy 2,72. (– 3,25) = – 8,84

b) (– 0,827). (–1,1) = 0,827. 1,1

$\begin{array}{l}\times \underset{¯}{\begin{array}{l}0,827\\ 1,1\end{array}}\\ 0827\\ 0827 \\ \overline{ 0,9097}\end{array}$

Vậy (– 0,827). (–1,1) = 0,9097

Toán lớp 6 trang 32 Vận dụng 2: Mức tiêu thụ nhiên liệu của một chiếc xe máy là 1,6 lít trên 100 kilômét. Giá một lít xăng E5 RON 92–ll ngày 20–10–2020 là 14 260 đồng (đã bao gồm thuế). Một người đi chiếc xe máy đó trên quãng đường 100 km thì sẽ hết bao nhiêu tiền xăng?

Lời giải: 

Số tiền xăng của người đi xe máy trên quãng đường 100km là:

14 260. 1,6 = 22 816 (đồng)

Vậy người đó đi quãng đường 100km hết 22 816 đồng tiền xăng.

Toán lớp 6 trang 32 Hoạt động 5: Tính: 31,5: 1,5

Lời giải: 

31,5: 1,5 = 315: 15

Vậy 31,5: 1,5 = 21

Toán lớp 6 trang 32 Hoạt động 6: Thực hiện các phép tính sau bằng cách quy về phép chia hai số thập phân dương tương tự như với số nguyên:

a) (– 31,5): 1,5

b) (– 31,5): (– 1,5).

Lời giải: 

a) (– 31,5): 1,5 = – (31,5: 1,5) = –21

b) (– 31,5): (– 1,5) = 31,5: 1,5 = 21

Giải Toán 6 trang 33 Tập 2

Toán lớp 6 trang 33 Câu hỏi: Thương của hai số khi nào là số dương? Khi nào là số âm?

Lời giải: 

+) Thương của hai số là số dương khi hai số cùng dấu nghĩa là hai số cùng dương hoặc cùng âm.

+) Thương của hai số là số âm khi hai số khác dấu nghĩa là một số âm, một số dương.

Toán lớp 6 trang 33 Luyện tập 3: Tính:

a) (– 5,24): 1,31;

b) (– 4,625): ( –1,25).

Lời giải: 

a) (–5,24): 1,31 = (–524): 131 = – (524: 131)

Vậy (– 5,24): 1,31 = –4.

b) (– 4,625): ( –1,25) = 4 625: 1 250

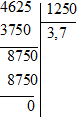
Vậy (– 4,625): ( –1,25) = 3,7

Toán lớp 6 trang 33 Vận dụng 3: Tài khoản vay ngân hàng của một chủ xưởng gỗ có số dư là –1,252 tỉ đồng. Sau khi chủ xưởng trả được một nửa khoản vay thì số dư trong tài khoản là bao nhiêu tỉ đồng?

Lời giải: 

Sau khi chủ xưởng nợ trả được một nửa khoản nợ thì số dư trong tài khoản là:

                 –1,252: 2= – 0,626 (tỉ đồng)

Vậy số dư trong tài khoản  của chủ xưởng gỗ là – 0,626 tỉ đồng.

Giải Toán 6 trang 34 Tập 2

Toán lớp 6 trang 34 Luyện tập 4: Tính giá trị của biểu thức sau:

21. 0,1 – [4 – (– 3,2 – 4,8)]: 0,1.

Lời giải: 

21. 0,1 – [4 – (– 3,2 – 4,8)]: 0,1

= 2,1 – [4 + (3,2 + 4,8)]: 0,1

= 2,1 – (4 + 8): 0,1

= 2,1 – 12: 0, 1

= 2,1– 120

= – (120 – 2,1)

= –117,9

Toán lớp 6 trang 34 Vận dụng 4: Từ độ cao – 0,21 km (so với mực nước biển), tàu thăm dò đáy biển bắt đầu lặn xuống. Biết rằng cứ sau mỗi phút, tàu lặn xuống sâu thêm được 0,021 km. Tính độ cao xác định vị trí tàu (so với mực nước biển) sau 10 phút kể từ khi tàu bắt đầu lặn.

Lời giải: 

Vì cứ sau mỗi phút, tàu lặn xuống sâu thêm được 0,021 km nghĩa là tàu đang ở vị trí – 0, 021 km so với mực nước biển.

Sau 10 phút tàu lặn sâu được:

 10. (– 0,021) = – 0,21(km)

Độ cao xác định vị trí tàu (so với mực nước biển) sau 10 phút kể từ khi tàu bắt đầu lặn là:

(– 0,21) + (– 0,21) = – (0,21 + 0,21) = – 0,42 (km)

Vậy độ cao xác định vị trí tàu (so với mực nước biển) sau 10 phút kể từ khi tàu bắt đầu lặn là – 0, 42km

Toán lớp 6 trang 34 Thử thách nhỏ: Thầy giáo viết lên bảng bốn số –3,2; – 0,75, 120; – 0,1 và yêu cầu mỗi học sinh chọn hai số rồi làm một phép tính với hai số đã chọn.

a) Mai làm phép trừ và nhận được kết quả là 120,75. Theo em, Mai đã chọn hai số nào?

b) Hà thực hiện phép chia và nhận được kết quả là 32. Em có biết Hà đã chọn hai số nào không?

Lời giải: 

a. Mai đã thực hiện phép trừ với 2 số sau: 120; –0,75

Mai thực hiện: 120 – (–0,75) = 120 + 0, 75 = 120,75

b. Hà đã chọn 2 số sau: –3,2; –0,1.

Hà thực hiện: (–3,2): (–0,1) = 3,2: 0,1 = 32: 1 = 32

Toán lớp 6 trang 34 Bài 7.5: Tính:

a) (–12, 245) + (–8, 235);

b) (– 8, 451) + 9, 79

c) (–11, 254) – (–7, 35).

Lời giải: 

a) (–12, 245) + (–8, 235) = – (12, 245 + 8, 235)

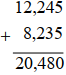
$\Rightarrow$ (–12, 245) + (–8, 235) = – (12, 245 + 8, 235) = –20,48

Vậy (–12, 245) + (–8, 235) = – 20, 48.

b) (– 8, 451) + 9, 79 = 9, 79 – 8, 451

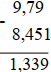
Vậy (– 8, 451) + 9, 79 = 1, 339

c) (–11, 254) – (–7, 35) = –11, 254 + 7,35 = – (11,254 – 7,35)

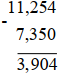
Vậy (–11, 254) – (–7, 35) = –3,904

Toán lớp 6 trang 34 Bài 7.6: Tính:

a) 8,625. (– 9);

b) (– 0,325). (– 2,35);

c) (– 9,5875): 2,95.

Lời giải: 

a) 8,625. (– 9) = – (8,625. 9)

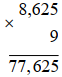
Vậy 8,625. (– 9) = – 77,625

b) (– 0,325). (– 2,35) = 0,326. 2,35

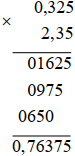
Vậy (– 0,325). (– 2,35) = 0,76375

c) (– 9,5875): 2,95 = – (9,5875: 2,95) = – (95 875: 29 500)

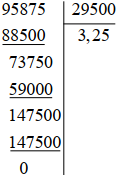
Vậy (– 9,5875): 2,95 = – 3,25

Toán lớp 6 trang 34 Bài 7.7: Để nhân (chia) một số thập phân với 0,1; 0,01; 0,001;... ta chỉ cần dịch dấu phẩy của số thập phân đó sang trái (phải) 1, 2, 3... hàng, chẳng hạn:

2,057. 0,1 = 0,2057

–31,025: 0,01 = –3 102,5.

Tính nhẩm:

a) (– 4,125). 0,01;

b) (– 28,45): (– 0,01).

Lời giải: 

a) (– 4,125). 0,01 = – (4,125. 0,01) = –0,04125 (ta dịch sang trái hai hàng).

b) (– 28,45): (– 0,01) = 28,45: 0,01 = 2 845 (ta dịch sang phải hai hàng).

Toán lớp 6 trang 34 Bài 7.8: Tính giá trị của các biểu thức sau:

a) 2,5. (4,1 – 3 – 2,5 + 2. 7,2) + 4,2: 2;

b) 2,86. 4 + 3,14. 4 – 6,01. 5 + 3².

Lời giải: 

a) 2,5. (4,1 – 3 – 2,5 + 2. 7,2) + 4,2: 2

= 2,5. (4,1 – 3 – 2,5 + 14,4) + 2,1

= 2,5. (1,1 – 2,5 + 14,4) + 2,1

= 2,5. [(1,1 + 14,4) – 2,5] + 2,1

= 2,5. (15,5 – 2,5) + 2,1

= 2,5. 13 + 2,1

= 32, 5 + 2,1

= 34,6

b) 2,86. 4 + 3,14. 4 – 6,01. 5 + 3²

= 4. (2,86 + 3, 14) – 30,05 + 9

= 4. 6 – 30,05 + 9

= 24 – 30,05 + 9

= (24 + 9) – 30,05

= 33 – 30,05

= 2,95

Toán lớp 6 trang 34 Bài 7.9: Điểm đông đặc và điểm sôi của thuỷ ngân lần lượt là – 38,83°C và 356,73°C. Một lượng thuỷ ngân đang để trong tủ bảo quản ở nhiệt độ – 51,2°C.

a) Ở nhiệt độ đó, thuỷ ngân ở thể rắn, thể lỏng hay thể khí?

b) Nhiệt độ của tủ phải tăng thêm bao nhiêu độ để lượng thuỷ ngân đó bắt đầu bay hơi?

Lời giải: 

a) Vì 38,83 < 51, 2 nên –38,83 > –51,2

Vậy thủy ngân đang ở thể rắn.

b) Để thủy ngân bắt đầu bay hơi phải tăng nhiệt độ tủ tăng thêm:

356,73 – (–51,2) = 356,73 + 51,2 = 407,93 (°C)

Vậy nhiệt độ của tủ tăng thêm 407,93 °C để lượng thủy ngân đó bắt đầu bay hơi.

Toán lớp 6 trang 34 Bài 7.10: Một khối nước đá có nhiệt độ –4,5°C. Nhiệt độ của khối nước đá đó phải tăng thêm bao nhiêu độ để chuyển thành thể lỏng? (Biết điểm nóng chảy của nước đá là 0 ^oC)

Lời giải: 

Nhiệt độ của khối nước đá đó phải tăng thêm số độ để chuyển thành thể lỏng là:

0 – (–4,5) = 4,5 (^oC)

Vậy nhiệt độ của khối nước đá đó phải tăng thêm 4,5 ^oC.

Toán lớp 6 trang 34 Bài 7.11: Năm 2018, ngành giấy Việt Nam sản xuất được 3,674 triệu tấn. Biết rằng để sản xuất ra 1 tấn giấy phải dùng hết 4,4 tấn gỗ. Em hãy tính xem năm 2018 Việt Nam đã phải dùng bao nhiêu tấn gỗ cho sản xuất giấy.

(Theo vppa.vn)

Lời giải: 

Đổi 3,674 triệu tấn = 3 674 000 tấn 

Năm 2018 Việt Nam đã phải dùng số tấn gỗ cho sản xuất giấy là:

3 674 000. 4,4 = 16 165 600(tấn gỗ)

Vậy năm 2018 Việt Nam đã phải dùng 16 165 600 tấn gỗ cho sản xuất giấy.

Xem thêm các bài giải SGK Toán 6 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 6

Bài 28: Số thập phân

Bài 30: Làm tròn và ước lượng

Bài 31: Một số bài toán về tỉ số và tỉ số phần trăm

Luyện tập chung trang 41