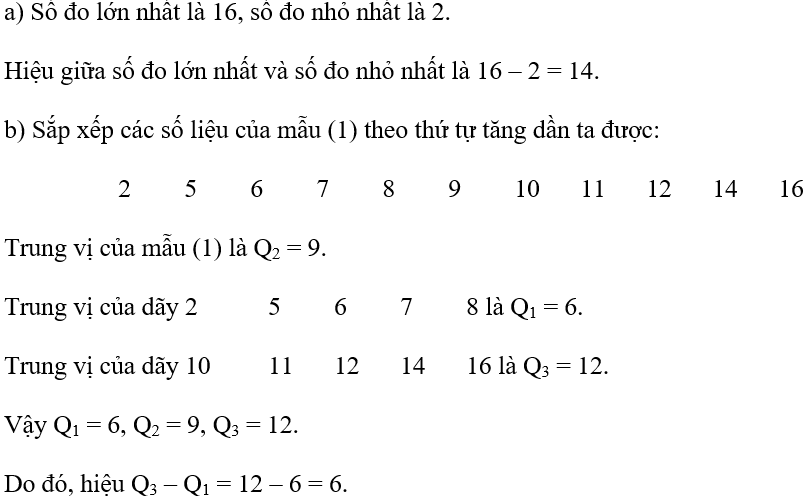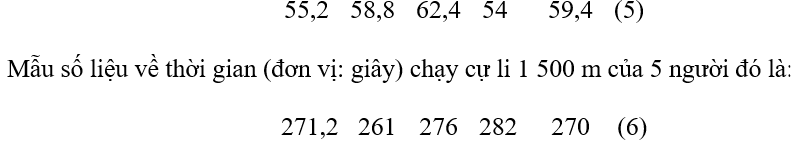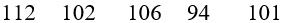Giải SGK Toán 10 (Cánh diều) Bài 3: Các số liệu đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm

Giải Toán 10 Bài 3: Các số liệu đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm

Câu hỏi khởi động trang 35 Toán lớp 10 Tập 2: Kết quả 5 bài kiểm tra môn Toán của hai bạn Dũng và Huy được thống kê trong bảng sau:

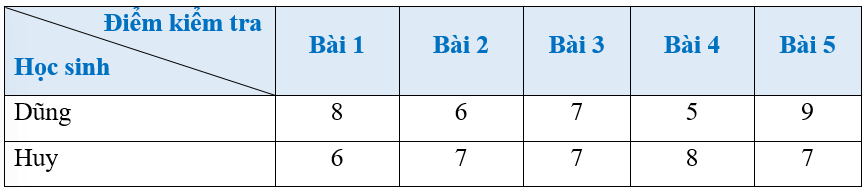
Kết quả làm bài kiểm tra môn Toán của bạn nào đồng đều hơn?

Lời giải:

Sau bài học này, ta giải quyết được bài toán trên như sau:

Số trung bình cộng điểm kiểm tra của bạn Dũng là:

$\overline{x_D}=\frac{8+6+7+5+9}{5}=7$

Phương sai mẫu số liệu điểm kiểm tra của bạn Dũng là:

$s_D^2=\frac{{\left(8-7\right)}^2+{\left(6-7\right)}^2+{\left(7-7\right)}^2+{\left(5-7\right)}^2+{\left(9-7\right)}^2}{5}=2$

Số trung bình cộng điểm kiểm tra của bạn Huy là:

$\overline{x_H}=\frac{6+7+7+8+7}{5}=7$

Phương sai mẫu số liệu điểm kiểm tra của bạn Huy là:

$s_H^2=\frac{{\left(6-7\right)}^2+{\left(7-7\right)}^2+{\left(7-7\right)}^2+{\left(8-7\right)}^2+{\left(7-7\right)}^2}{5}=\frac{2}{5}=0,4$

Vì 0,4 < 2 nên $s_H^2<s_D^2$ nên bạn Huy có kết quả kiểm tra môn Toán đồng đều hơn bạn Dũng.

I. Khoảng biến thiên, khoảng tứ phân vị

Hoạt động 1 trang 35 Toán lớp 10 Tập 2: Kết quả của 11 lần đo được thống kê trong mẫu số liệu sau:

a) Tìm hiệu giữa số đo lớn nhất và số đo nhỏ nhất.

b) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần. Tìm các giá trị Q­₁, Q­₂, Q₃ là tứ phân vị của mẫu đó. Sau đó, tìm hiệu Q₃ – Q₁.

Lời giải:

Hoạt động 2 trang 37 Toán lớp 10 Tập 2: Số liệu thống kê kết quả 5 bài kiểm tra môn Toán của bạn Dũng là:

Số trung bình cộng của mẫu số liệu (3) là:

$\overline{x}=\frac{8+6+7+5+9}{5}=7$

a) Tính các độ lệch sau: (8 – 7); (6 – 7); (7 – 7); (5 – 7); (9 – 7).

b) Tính bình phương các độ lệch và tính trung bình cộng của chúng.

Lời giải:

a) Ta tính được các độ lệch là: (8 – 7) = 1; (6 – 7) = – 1; (7 – 7) = 0; (5 – 7) = – 2; (9 – 7) = 2.

b) Bình phương các độ lệch là: (8 – 7)² = 1² = 1; (6 – 7)² = (– 1)² = 1; (7 – 7)² = 0² = 0; (5 – 7) = (– 2)² = 4; (9 – 7)² = 2² = 4.

Trung bình cộng của bình phương các độ lệch là:

$\frac{{\left(8-7\right)}^2+{\left(6-7\right)}^2+{\left(7-7\right)}^2+{\left(5-7\right)}^2+{\left(9-7\right)}^2}{5}=\frac{1+1+0+4+4}{5}=2$

Luyện tập 1 trang 38 Toán lớp 10 Tập 2: Mẫu số liệu về thời gian (đơn vị: giây) chạy cự li 500 m của 5 người là:

Tính phương sai của mẫu (5) và mẫu (6). Từ đó cho biết cự li chạy nào có kết quả đồng đều hơn.

Lời giải:

Số trung bình cộng của mẫu số liệu (5) là:

$\overline{x_{\left(5\right)}}=\frac{55,2+58,8+62,4+54+59,4}{5}=57,96$

Phương sai của mẫu số liệu (5) là:

$s_{\left(5\right)}^2=\frac{{\left(55,2-57,96\right)}^2+{\left(58,8-57,96\right)}^2+{\left(62,4-57,96\right)}^2+{\left(54-57,96\right)}^2+{\left(59,4-57,96\right)}^2}{5}$

= 9,1584.

Số trung bình cộng của mẫu số liệu (6) là:

$\overline{x_{\left(6\right)}}=\frac{271,2+261+276+282+270}{5}=272,04$

Phương sai của mẫu số liệu (6) là:

$s_{\left(6\right)}^2=\frac{1}{5}$[(271,2 − 272,04)²+ (261 − 272,04)²+ (276 − 272,04)²+ (282 − 272,04)²+ (270 − 272,04)²] = 48,3264.

Vì 9,1584 < 48,3264 nên $s_{\left(5\right)}^2<s_{\left(6\right)}^2$.

Vậy cự li chạy 500 m có kết quả đồng đều hơn.

Hoạt động 3 trang 39 Toán lớp 10 Tập 2: Trong Ví dụ 2, phương sai của mẫu số liệu (4) là $s_H^2=0,4$. Tính $s_H=\sqrt{s_H^2}$.

Lời giải:

Ta có: $s_H=\sqrt{s_H^2}=\sqrt{0,4}=\frac{\sqrt{10}}{5}\approx 0,63$.

Luyện tập 2 trang 39 Toán lớp 10 Tập 2: Mẫu số liệu về số lượng áo bán ra lần lượt từ tháng 1 đến tháng 12 của một doanh nghiệp là:

Tính độ lệch chuẩn của mẫu số liệu đó.

Lời giải:

Số trung bình cộng của mẫu số liệu trên là:

$\overline{x}=\frac{430+560+450+550+760+430+525+410+635+450+800+900}{12}=575$.

Phương sai của mẫu số liệu trên là:

$s^2=\frac{1}{12}$[(430 − 575)² + (560 − 575)² + (450 − 575)² + (550 − 575)² + (760 – 575)² + (430 − 575)² + (525 – 575)² + (410 − 575)² + (635 − 575)² + (450 − 575)² + (800 − 575)² + (900 – 575)²] ≈ 24829,17.

Vậy độ lệch chuẩn của mẫu số liệu trên là: s = $\sqrt{s^2}=\sqrt{24829,27}\approx 157,57$.

Bài tập

Bài 1 trang 41 Toán lớp 10 Tập 2: Trong 5 lần nhảy xa, hai bạn Hùng và Trung có kết quả (đơn vị: mét) lần lượt là

a) Kết quả trung bình của hai bạn có bằng nhau hay không?

b) Tính phương sai của mẫu số liệu thống kê kết quả 5 lần nhảy xa của mỗi bạn. Từ đó cho biết bạn nào có kết quả nhảy xa ổn định hơn.

Lời giải:

a) Kết quả trung bình của Hùng là:

$\overline{x_H}=\frac{2,4+2,6+2,4+2,5+2,6}{5}=2,5$.

Kết quả trung bình của Trung là:

$\overline{x_T}=\frac{2,4+2,6+2,4+2,5+2,6}{5}=2,5$.

Vậy kết quả trung bình của hai bạn có bằng nhau.

b) Phương sai mẫu số liệu kết quả nhảy xa của bạn Hùng là:

$s_H^2=\frac{{\left(2,4-2,5\right)}^2+{\left(2,6-2,5\right)}^2+{\left(2,4-2,5\right)}^2+{\left(2,5-2,5\right)}^2+{\left(2,6-2,5\right)}^2}{5}=0,008$.

Phương sai mẫu số liệu kết quả nhảy xa của bạn Trung là:

$s_T^2=\frac{{\left(2,4-2,5\right)}^2+{\left(2,5-2,5\right)}^2+{\left(2,5-2,5\right)}^2+{\left(2,5-2,5\right)}^2+{\left(2,6-2,5\right)}^2}{5}=0,004$.

Vì 0,04 < 0,08 nên $s_T^2<s_H^2$.

Vậy bạn Trung có kết quả nhảy xa ổn định hơn.

Bài 2 trang 41 Toán lớp 10 Tập 2: Biểu đồ đoạn thẳng ở Hình 3 biểu diễn tốc độ tăng trưởng GDP của Việt Nam giai đoạn 2012 – 2019.

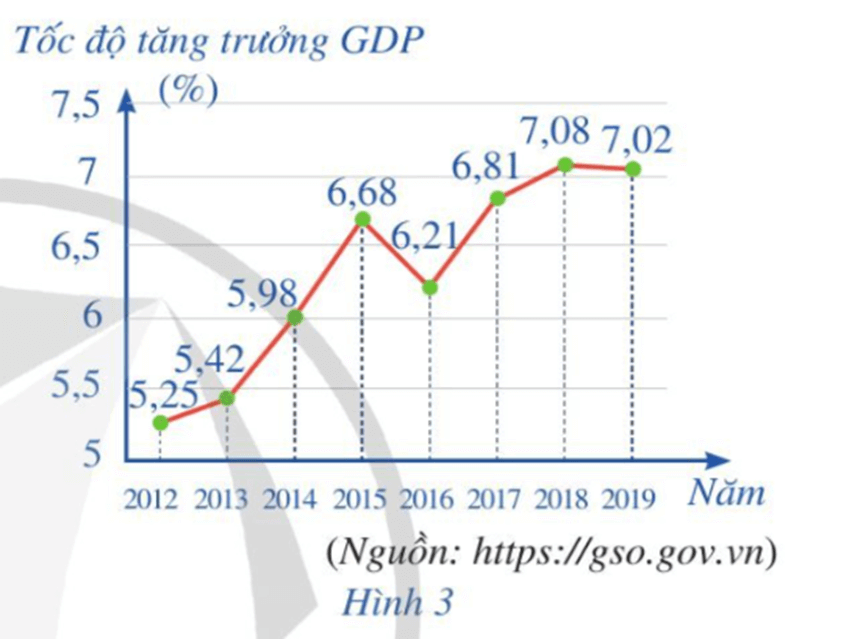
a) Viết mẫu số liệu thống kê tốc độ tăng trưởng GDP nhận được từ biểu đồ ở Hình 3.

b) Tìm khoảng biến thiên của mẫu số liệu đó.

c) Tìm khoảng tứ phân vị của mẫu số liệu đó.

d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.

Lời giải:

Bài 3 trang 41 Toán lớp 10 Tập 2: Biểu đồ đoạn thẳng ở Hình 4 biểu diễn giá vàng bán ra trong bảy ngày đầu tiên của tháng 6 năm 2021.

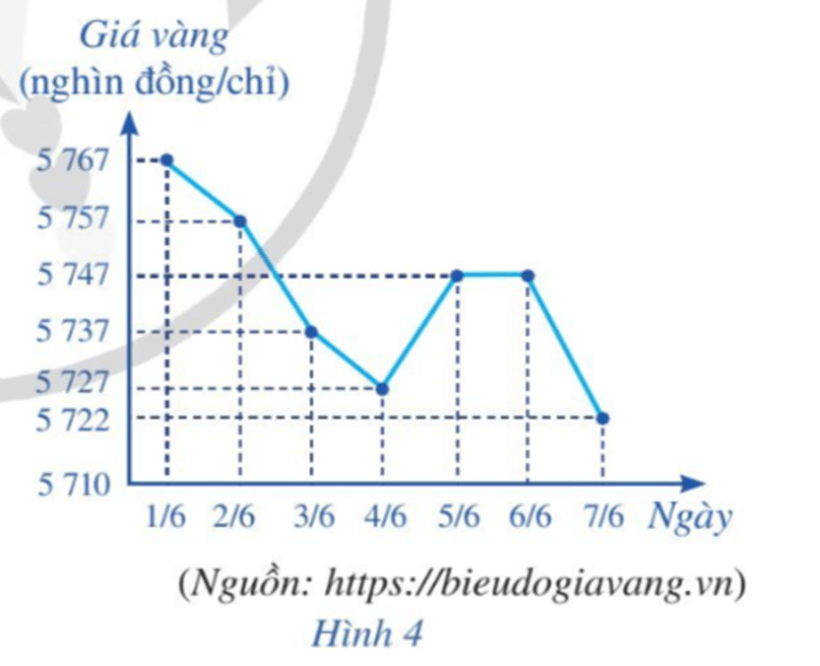
a) Viết mẫu số liệu thống kê giá vàng bán ra nhận được từ biểu đồ ở Hình 4.

b) Tìm khoảng biến thiên của mẫu số liệu đó.

c) Tìm khoảng tứ phân vị của mẫu số liệu đó.

d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.

Lời giải:

Bài 4 trang 41 Toán lớp 10 Tập 2: Để biết cây đậu phát triển như thế nào sau khi gieo hạt, bạn Châu gieo 5 hạt đậu vào 5 chậu riêng biệt và cung cấp cho chúng lượng nước, ánh sáng như nhau. Sau hai tuần, 5 hạt đậu đã nảy mầm và phát triển thành 5 cây con. Bạn Châu đo chiều cao từ rễ đến ngọn của mỗi cây (đơn vị: mi-li-mét) và ghi kết quả là mẫu số liệu sau:

a) Tính phương sai và độ lệch chuẩn của mẫu số liệu trên.

b) Theo em, các cây có phát triển đồng đều hay không?

Lời giải:

a) Số trung bình cộng của mẫu số liệu đã cho là:

$\overline{x}=\frac{112+102+106+94+101}{5}=103$.

Phương sai của mẫu số liệu trên là:

$s^2=\frac{{\left(112-103\right)}^2+{\left(102-103\right)}^2+{\left(106-103\right)}^2+{\left(94-103\right)}^2+{\left(101-103\right)}^2}{5}=35,2$.

Độ lệch chuẩn của mẫu số liệu là:

s = $\sqrt{s^2}=\sqrt{35,2}=\frac{4\sqrt{55}}{5}\approx 5,93$.

b) Vì độ lệch chuẩn của mẫu số liệu là khoảng 5,93, số này khá lớn, chính vì vậy các cây phát triển không đồng đều.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 1: Số gần đúng. Sai số

Bài 2: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm

Bài 4: Xác suất của biến cố trong một số trò chơi đơn giản

Bài 5: Xác suất của biến cố

Bài tập cuối chương 6