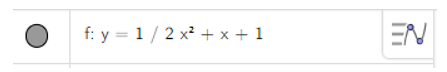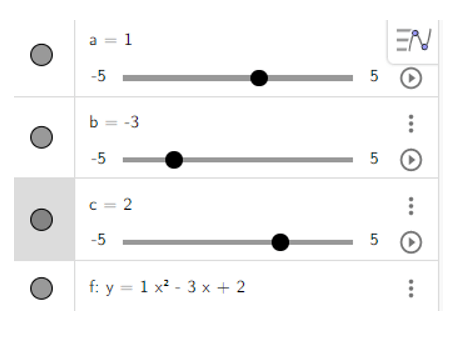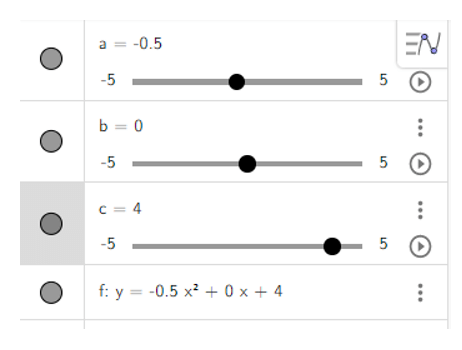Giải SGK Toán 10 (Chân trời sáng tạo) Bài 1: Vẽ đồ thị hàm số bậc hai bằng phần mềm Geogebra

Giải Toán 10 Bài 1: Vẽ đồ thị hàm số bậc hai bằng phần mềm Geogebra

Hoạt động 1. Vẽ đồ thị hàm số y = ax² + bx + c với a, b, c nhập từ bàn phím

Thực hành 1 trang 88 Toán lớp 10 Tập 2: Vẽ đồ thị các hàm bậc hai sau:

a) y = – x² + 4x – 3;

b) y = x² + 2;

c) y = $\frac{1}{2}$x² + x + 1;

d) y = x² – 4x + 4.

Lời giải:

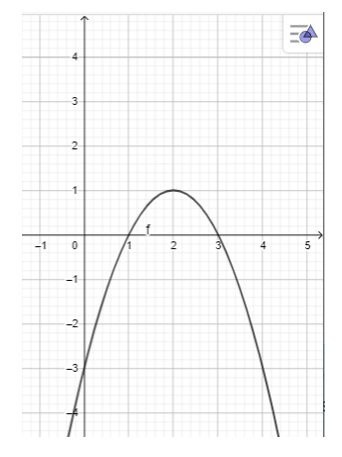
a) y = – x² + 4x – 3;

Bước 1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online.

Bước 2. Các bước thao tác trên Geogebra:

Nhập phương trình bậc hai theo cú pháp y = – x^2 + 4x – 3 vào vùng nhập lệnh.

Ta được hình vẽ sau:

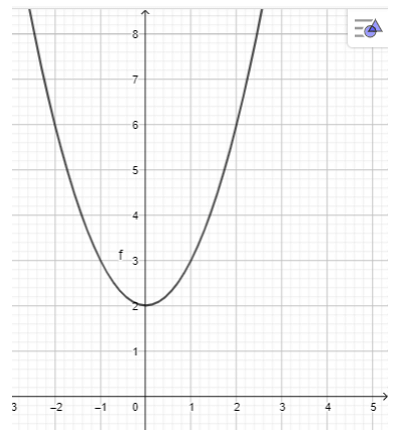
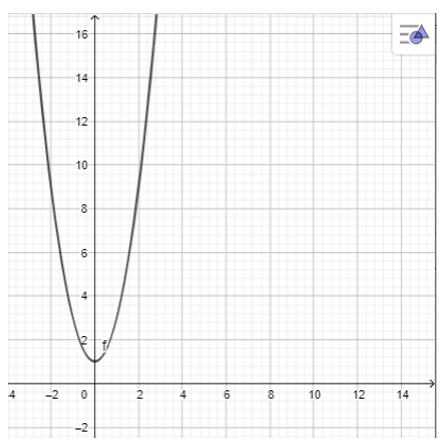
b) y = x² + 2;

Bước 1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online.

Bước 2. Các bước thao tác trên Geogebra:

Nhập phương trình bậc hai theo cú pháp y = x^2 + 2 vào vùng nhập lệnh.

Khi đó ta có hình vẽ:

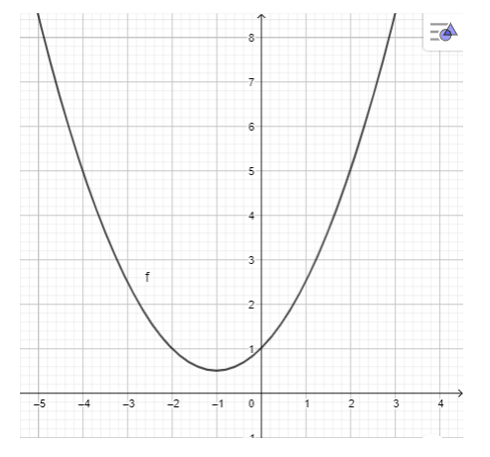
c) y = $\frac{1}{2}$x² + x + 1;

Bước 1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online.

Bước 2. Các bước thao tác trên Geogebra:

Nhập phương trình bậc hai theo cú pháp y = 1/2x^2 + x + 1 vào vùng nhập lệnh.

Khi đó ta có hình vẽ sau:

d) y = x² – 4x + 4.

Bước 1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online.

Bước 2. Các bước thao tác trên Geogebra:

Nhập phương trình bậc hai theo cú pháp y = x^2 – 4x + 4 vào vùng nhập lệnh.

Khi đó ta có hình vẽ sau:

Hoạt động 2. Vẽ parabol với tham số thay đổi bằng thanh trượt

Thực hành 2 trang 89 Toán lớp 10 Tập 2: Điều chỉnh a, b, c để vẽ được nhiều dạng parabol khác nhau:

a) y = x² – 3x + 2;

b) y = x²;

c) y = -x²;

d) y = 2x² + 1;

e) y = $-\frac{1}{2}$x² + 4.

Lời giải:

Bước 1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web https://www.geogebra.org để sử dụng phiên bản online.

Bước 2. Các bước thao tác trên Geogebra:

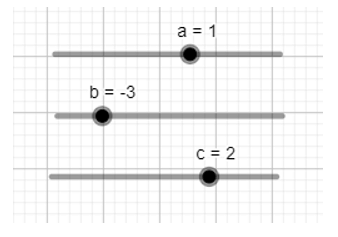
- Tạo các thanh trượt biểu thị các tham số a, b, c bằng cách nhấp chuột liên tiếp vào thanh công cụ  và vào vị trí màn hình nơi mà ta muốn đặt thanh trượt.

- Nhập công thức hàm số bậc hai y = ax² + bx + c tại vùng nhập lệnh theo cú pháp: y = ax^2 + bx + c.

- Nhập công thức ∆ = b² – 4ac bằng cách gõ D = b^2 – 4ac.

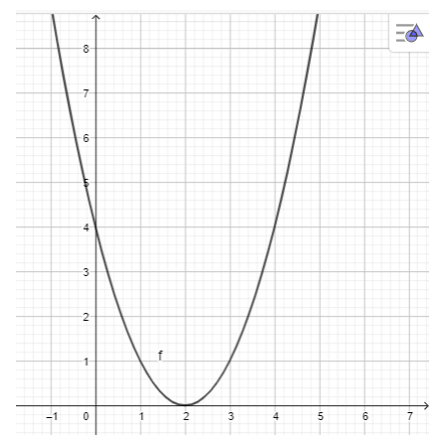
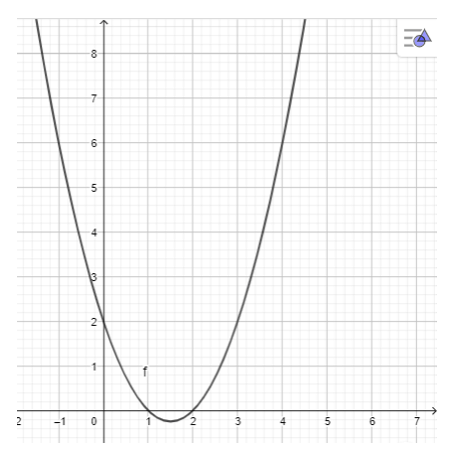
a) y = x² – 3x + 2

- Dùng chuột điểu chình các thanh trượt a, b, c để a = 1, b = -3, c = 2 ta được hình vẽ sau:

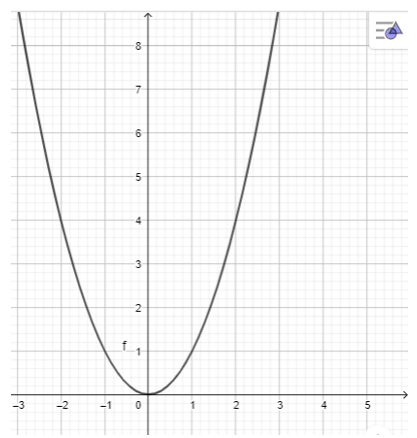
b) y = x²

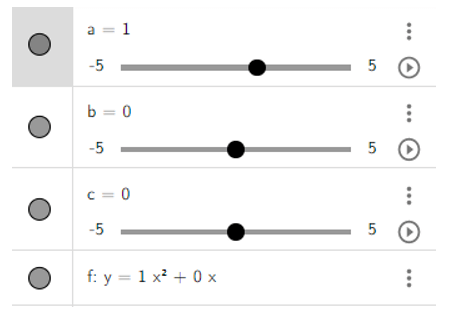
- Dùng chuột điểu chình các thanh trượt a, b, c để a = 1, b = 0, c = 0 ta được hình vẽ sau:

c) y = -x²

- Dùng chuột điểu chình các thanh trượt a, b, c để a = -1, b = 0, c = 0 ta được hình vẽ sau:

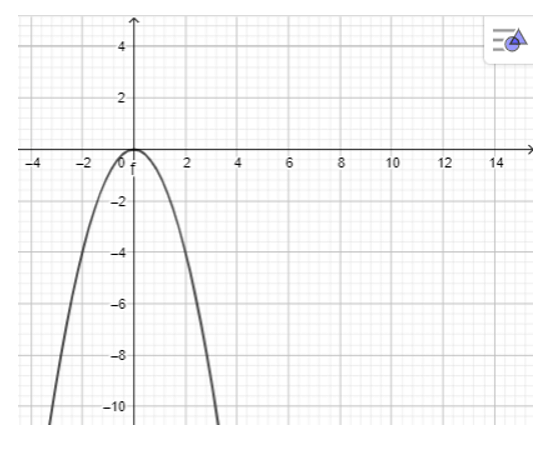
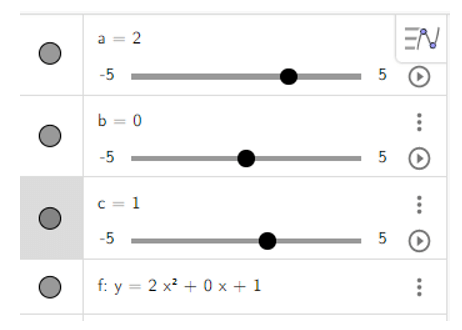
d) y = 2x² + 1;

- Dùng chuột điểu chình các thanh trượt a, b, c để a = 2, b = 0, c = 1 ta được hình vẽ sau:

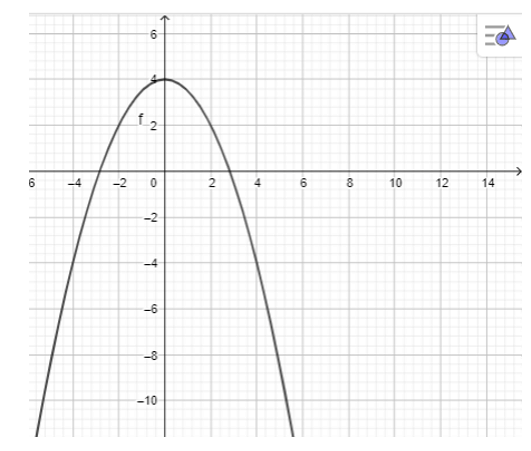
e) y = $-\frac{1}{2}$>x² + 4.

- Dùng chuột điểu chình các thanh trượt a, b, c để a = $-\frac{1}{2}$, b = 0, c = 4 ta được hình vẽ sau:

Hoạt động 3. Vẽ cổng chào hình parabol

Thực hành 3 trang 90 Toán lớp 10 Tập 2: Hãy tự thiết kế một cổng trào hình parabol.

Một cổng chào hình parabol có chiều cao là 8,1m và khoảng cách giữa hai chân cổng là 10m. Hãy vẽ parabol đó.

Lời giải:

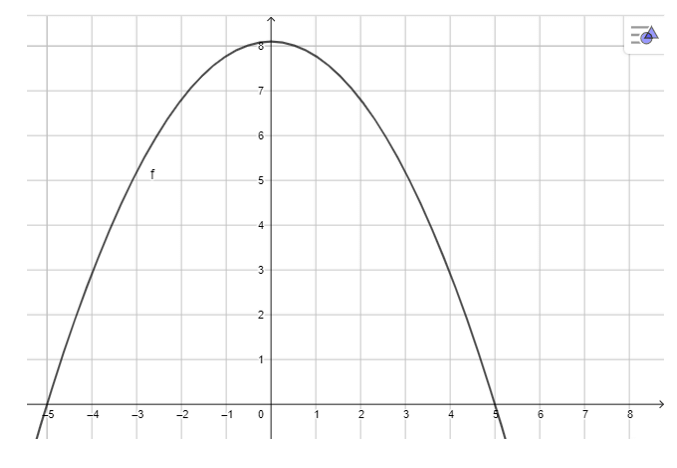
- Ta chọn hệ tọa độ để parabol có phương trình y = - ax² + h.

- Ta có h = 8,1m, d = 10m, suy ra điểm M(5; 0) thuộc parabol.

- Thay tọa độ điểm M vào phương trình parabol ta được: 0 = - a.5² + 8,1 ⇔ a = 0,324.

- Vậy phương trình parabol là y = -0,324x² + 8,1.

- Dùng Geogebra theo cách vẽ đồ thị hàm số bậc hai đã hướng dẫn trong Hoạt động 1, ta vẽ được parabol biểu diễn cổng chào như hình sau:

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 9

Bài 1: Không gian mẫu và biến cố

Bài 2: Xác suất của biến cố

Bài tập cuối chương 10

Bài 2: Vẽ ba đường conic bằng phần mềm Geogebra