Cho tam giác ABC vuông tại đỉnh A. Gọi AD là đường cao của tam giác. Biết rằng BD = 2 cm, CD = 8 cm

Bài 9.37 trang 60 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại đỉnh A. Gọi AD là đường cao của tam giác. Biết rằng BD = 2 cm, CD = 8 cm. Hãy tính độ dài các cạnh AB, AC và chiều cao AD của tam giác ABC.

Trả lời

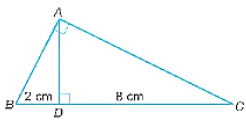
Vì AD là đường cao của tam giác ABC nên AD vuông góc với BC.

Do đó, $\widehat{ADB}=\widehat{ADC}=90°$  .

Tam giác ABD và tam giác CAD có:

$\widehat{ADB}=\widehat{ADC}=90°$ (cmt)

 $\widehat{BAD}=\widehat{C}$ (cùng phụ với góc DAC).

Do đó, ∆ABD ᔕ ∆CAD (g.g).

Suy ra $\frac{AD}{CD}=\frac{BD}{AD}$  nên AD² = CD . BD = 8 . 2 = 16.

Do đó, AD = 4 cm.

Áp dụng định lý Pythagore trong tam giác vuông ABD vuông tại D có:

AB² = AD² + BD² = 4² + 2² = 20.

Nên AB = $2\sqrt{5}$ cm.

Áp dụng định lý Pythagore vào tam giác ACD vuông tại D có:

AC² = AD² + CD² = 4² + 8² = 80.

Nên AC = $4\sqrt{5}$  cm.

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Bài 33: Hai tam giác đồng dạng

Bài 34: Ba trường hợp đồng dạng của hai tam giác

Bài 35: Định lí Pythagore và ứng dụng

Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Bài 37: Hình đồng dạng

Bài tập cuối chương 9