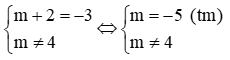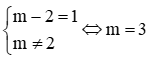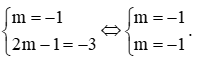Giải SBT Toán 8 (Chân trời sáng tạo) Bài tập cuối chương 5 trang 18

Giải SBT Toán 8 Bài tập cuối chương 5 trang 18

Câu hỏi trắc nghiệm

Bài 1 trang 18 SBT Toán 8 Tập 2: Trong các hàm số sau, hàm số nào là hàm số bậc nhất?

A.$y=1-\frac{1}{x}$.

B.$y=2-\frac{2x}{3}$.

C. y = x² + 1.

D. y = 2$\sqrt{x}$+1.

Lời giải:

Đáp án đúng là: B

Vì hàm số $y=2-\frac{2x}{3}$ có dạng y = ax + b với a = $\frac{-2}{3}$ và b = 2.

Bài 2 trang 18 SBT Toán 8 Tập 2: Trong các điểm sau, điểm nào thuộc đồ thị hàm số y = 2 – 4x?

A. (1; 1).

B. (2; 0).

C. (1; –1).

D. (1; –2).

Lời giải:

Đáp án đúng là: D

Thay điểm có toạ độ (1; –2) vào hàm số y = 2 – 4x ta có: –2 = 2 – 4.(1) $\Rightarrow$ thoả mãn

Do đó điểm có toạ độ (1; –2) thuộc hàm số y = 2 – 4x.

Bài 3 trang 18 SBT Toán 8 Tập 2: Nếu hai đường thẳng d₁: y = –3x + 4 và d₂: y = (m + 2)x + m song song với nhau thì m bằng:

A. –2.

B. 3.

C. –5.

D. –3.

Lời giải:

Đáp án đúng là: C

Để d₁ song song d₂ thì 

Bài 4 trang 18 SBT Toán 8 Tập 2: Đường thẳng song song với đường thẳng y = 5x và cắt trục tung tại điểm có tung độ bằng 1 là

A. y = 5x – 1.

B. y = –5x – 1.

C. y = 5x + 1.

D. y = 4 – 5(1 – x).

Lời giải:

Đáp án đúng là: C

Đường thẳng y = ax + b song song với đường thẳng y = 5x nên a = 5.

Đường thẳng y = 5x + b cắt trục tung tại điểm M có tung độ bằng 1 hay M(0; 1).

Thay M(0; 1) vào y = 5x + b ta có: 1 = 5.0 + b $\iff$ b = 1.

Suy ra hàm số cần tìm là y = 5x + 1.

Bài 5 trang 18 SBT Toán 8 Tập 2: Cho hai đường thẳng y = $\frac{1}{4}$x + 4và y = $\frac{1}{4}$x - 4. Hai đường thẳng đã cho:

A. Cắt nhau tại điểm có hoành độ là 4.

B. Song song với nhau.

C. Cắt nhau tại điểm có tung độ là 4.

D. Trung nhau.

Lời giải:

Đáp án đúng là: B

Ta có: y = $\frac{1}{4}$x + 4 và y = $\frac{1}{4}$x - 4

Vì  nên đường thẳng y = $\frac{1}{4}$x + 4 song song với đường thẳng y = $\frac{1}{4}$x - 4.

Bài 6 trang 18 SBT Toán 8 Tập 2: Cho hàm số $y=\frac{-x+9}{9}$. Phát biểu nào sau đây là đúng về đồ thị hàm số đã cho?

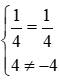
A. Là một đường thẳng có hệ số b là 9.

B. Không phải là một đường thẳng.

C. Cắt trục hoành tại điểm có hoành độ là 9.

D. Đi qua điểm (19; 1).

Lời giải:

Đáp án đúng là: C

Ta có: $y=\frac{-x+9}{9}$.

Xét x = 9 thay vào y ta được: $y=\frac{-9+9}{9}=0$.

Do đó đồ thị hàm số $y=\frac{-x+9}{9}$ cắt trục hoành tại điểm có hoành độ là 9.

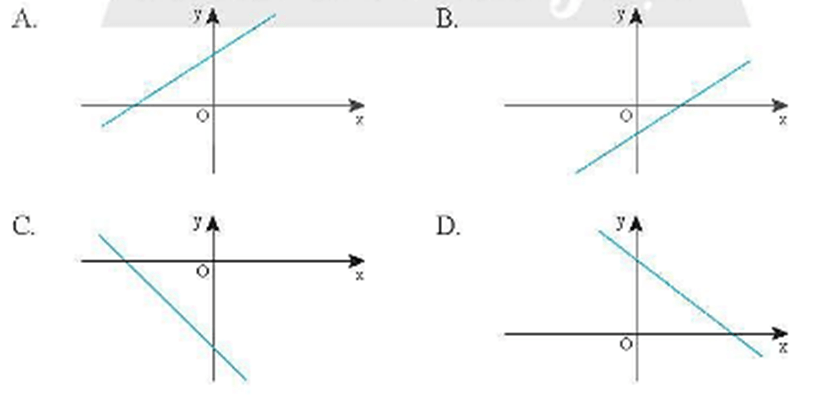
Bài 7 trang 18 SBT Toán 8 Tập 2: Đồ thị của hàm số y = $\frac{x}{4}$ + 4 có dạng giống với đồ thị nào dưới đây?

Lời giải:

Đáp án đúng là: A

Ta có: y = $\frac{x}{4}$ + 4

•Với x = 0 thay vào y ta được y = $\frac{0}{4}$ + 4 = 4

•Với y = 0 thay vào hàm số y = $\frac{x}{4}$ + 4ta có:

0 = $\frac{x}{4}$+ 4 $\iff$x = -1

Do đó đồ thị hàm số y = $\frac{x}{4}$ + 4đi qua 2 điểm có toạ độ (0; 4) và (–1; 0) nên đồ thị có dạng như đáp án A.

Bài 8 trang 19 SBT Toán 8 Tập 2: Đoạn thẳng trong hình vẽ bên là tập hợp những điểm (x; y) thoả mãn điều kiện nào dưới đây?

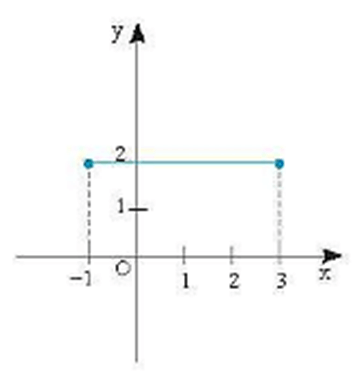
A. –1 $\le$ y $\le$ 3 và x = 2.

B. –1 £ x $\le$ 3 và y $\le$ 2.

C. –1 $\le$ x $\le$ 3 và y = 2.

D. x ≥ –1 và y = 2.

Lời giải:

Đáp án đúng là: C

Dựa vào hình vẽ ta thấy đoạn thẳng đi qua các điểm có tung độ y = 2 và có hoành độ nằm trong đoạn [–1; 3].

Bài 9 trang 19 SBT Toán 8 Tập 2: Cho hàm số y = 5x + 10. Giá trị của hàm số tại x = a – 1 là:

A. 5a + 5.

B. 5a + 15.

C. 5a + 3.

D. 5a – 5.

Lời giải:

Đáp án đúng là: A

Thay x = a – 1 vào hàm số y = 5x + 10, ta được:

y = 5(a – 1) + 10 = 5a – 5 + 10 = 5a + 5.

Bài tập tự luận

Bài 10 trang 19 SBT Toán 8 Tập 2: Cho hàm số y = f(x) = 3x – 2. Tính f(–5); f(–4); f(0); f(1); f(2); f(a); f(a + 1).

Lời giải:

Ta có: y = f(x) = 3x – 2.

•Thay x = –5 vào f(x) ta được: f(–5) = 3.(–5) – 2 = –17.

•Thay x = –4 vào f(x) ta được: f(–4) = 3.(–4) – 2 = –14.

•Thay x = 0 vào f(x) ta được: f(0) = 3.0– 2 = –2.

•Thay x = 1 vào f(x) ta được: f(1) = 3.1 – 2 = 1.

•Thay x = 2 vào f(x) ta được: f(2) = 3.2 – 2 = 4.

•Thay x = a vào f(x) ta được: f(a) = 3a – 2.

•Thay x = a + 1 vào f(x) ta được: f(a + 1) = 3(a + 1) – 2 = 3a + 1.

Vậy f(–5) = –17; f(–4) = –14; f(0) = –2; f(1) = 1; f(2) = 4; f(a) = 3a – 2; f(a + 1) = 3a + 1.

Bài 11 trang 19 SBT Toán 8 Tập 2: Cho hàm số y = f(x) = $\frac{2}{3}$x + 5. Tìm toạ độ giao điểm của đồ thị hàm số đã cho với trục Ox và trục Oy.

Lời giải:

•Đồ thị hàm số y = f(x) = $\frac{2}{3}$x + 5cắt Ox tại M nên y_M = 0.

Do đó: $\frac{2}{3}$x + 5 = 0 $\iff$$\frac{2}{3}$x = -5 $\iff$ x = $\frac{-15}{2}$.

Suy ra đồ thị hàm số y = f(x) = $\frac{2}{3}$x + 5 cắt Ox tại $M\left(\frac{-15}{2};0\right)$.

•Đồ thị hàm số y = f(x) = $\frac{2}{3}$x + 5 cắt Oy tại N nên x_N = 0.

Thay x_N = 0 vào f(x) ta có: y = $\frac{2}{3}$.0 + 5 = 5.

Suy ra đồ thị hàm số y = f(x) = $\frac{2}{3}$x + 5 cắt Oy tại N(0; 5).

Vậy đồ thị hàm số y = f(x) $\frac{2}{3}$x + 5 cắt Ox, Oy tại $M\left(\frac{-15}{2};0\right)$ và N(0; 5).

Bài 12 trang 19 SBT Toán 8 Tập 2: Cho hàm số y = f(x) = (m + 1)x + 5.

a) Tìm điều kiện của m để hàm số đã cho là hàm số bậc nhất.

b) Với giá trị nào của m thì đồ thị hàm số đã cho đi qua điểm A(5; 0)?

Lời giải:

a) Để y = f(x) = (m + 1)x + 5 là hàm số bậc nhất thì m + 1 $\ne$ 0 hay m $\ne$ –1.

Vậy điều kiện của m để hàm số đã cho là hàm số bậc nhất là m $\ne$ –1.

b) Vì đồ thị hàm số đã cho đi qua điểm A(5; 0) nên ta có:

0 = 5(m + 1) + 5

$\iff$ 5m + 10 = 0

$\iff$ m = –2

Vậy m = –2.

Bài 13 trang 19 SBT Toán 8 Tập 2: Cho hàm số y = (m – 3)x.

a) Với giá trị nào của m thì đồ thị hàm số đã cho đi qua điểm A(1; 2)?

b) Với giá trị nào của m thì đồ thị hàm số đã cho đi qua điểm B(1; –2)?

Lời giải:

a) Vì đồ thị hàm số đã cho đi qua điểm A(1; 2) nên ta có:

2 = 1(m – 3)

$\iff$ m – 3 = 2

$\iff$ m = 5

Vậy m = 5.

b) Vì đồ thị hàm số đã cho đi qua điểm B(1; –2) nên ta có:

–2 = 1.(m – 3)

$\iff$ m – 3 = –2

$\iff$ m = 1

Vậy m = 1.

Bài 14 trang 19 SBT Toán 8 Tập 2: Cho hai d: y = x – 2 và d’: y = –2x + 1.

a) Tìm hệ số góc của hai đường thẳng d và d’.

b) Tìm toạ độ giao điểm của hai đường thẳng d và d’ với trục Ox và Oy.

c) Với giá trị nào của m thì đồ thị hàm số y = (m – 2)x – m song song với d và cắt d’.

Lời giải:

a) Đường thẳng d: y = x – 2 có hệ số góc là a = 1.

Đường thẳng d’: y = –2x + 1 có hệ số góc là a = –2.

b) +) Xét hàm số y = x – 2

Đồ thị hàm số y = x – 2 cắt Ox tại M nên y_M = 0.

Do đó: x – 2 = 0 $\iff$ x = 2.

Suy ra đồ thị hàm số y = x – 2 cắt Ox tại M(2; 0).

Đồ thị hàm số y = x – 2 cắt Oy tại N nên x_N = 0.

Thay x_N = 0 vào f(x) ta có: y = 0 – 2 = –2.

Suy ra đồ thị hàm số y = x – 2 cắt Oy tại N(0; –2).

+) Xét hàm số y = –2x + 1.

Đồ thị hàm số y = –2x + 1 cắt Ox tại P nên y_P = 0.

Do đó: -2x + 1 = 0 $\iff$ x = $\frac{1}{2}$

Suy ra đồ thị hàm số y = –2x + 1 cắt Ox tại $P\left(\frac{1}{2};0\right)$.

Đồ thị hàm số y = –2x + 1 cắt Oy tại Q nên x_Q = 0.

Thay x_Q = 0 vào f(x) ta có: y = –2.0 + 1 = 1.

Suy ra đồ thị hàm số y = –2x + 1 cắt Oy tại Q(0; 1).

Vậy đồ thị hàm số y = x – 2 cắt Ox, Oy tại M(2; 0) và N(0; –2).

Đồ thị hàm số y = –2x + 1 cắt Ox, Oy tại $P\left(\frac{1}{2};0\right)$ và Q(0; 1).

c) Đồ thị hàm số y = (m – 2)x – m cắt d’: y = –2x + 1 nên m – 2 $\ne$ –2 $\iff$ m $\ne$ 0.

Đồ thị hàm số y = (m – 2)x – m song song với d: y = x – 2 thì

Vậy m = 3 thoả mãn đề bài.

Bài 15 trang 19 SBT Toán 8 Tập 2: Cho đường thẳng d: y = (m – 2)x + 1. Với giá trị nào của m để:

a) Đường thẳng d song song với đường thẳng d₁: y = 2x + 3.

b) Đường thẳng d cắt đường thẳng d₂: y = –5x + 1.

Lời giải:

a) Đường thẳng y = (m – 2)x + 1 song song với đường thẳng y = 2x + 3.

Suy ra m – 2 = 2 $\iff$ m = 4.

Vậy m = 4.

b) Đường thẳng y = (m – 2)x + 1 cắt đường thẳng y = –5x + 1.

Suy ra m – 2 $\ne$ –5 $\iff$ m $\ne$ –3.

Vậy m $\ne$ –3.

Bài 16 trang 19 SBT Toán 8 Tập 2: Xác định hàm số y = ax + b biết đồ thị của hàm số đã cho song song với đường thẳng y = –2x + 3 và đi qua A(1; –3).

Lời giải:

Đồ thị của hàm số y = ax + b song song với đường thẳng y = –2x + 3 nên a = –2 và b $\ne$ 3.

Ta được hàm số y = –2x + b.

Đồ thị của hàm số y = –2x + b đi qua A(1; –3) nên ta có:

–3 = –2.1 + b $\iff$ b = –1.

Vậy hàm số cần tìm có phương trình y = –2x – 1.

Bài 17 trang 19 SBT Toán 8 Tập 2: Tìm điểm cố định mà mỗi đường thẳng d’: y = (m – 2)x + 3 luôn đi qua với mọi giá trị của m.

Lời giải:

Giả sử điểm cố định của đồ thị hàm số y = (m – 2)x + 3 là I(x₀; y₀).

Thay x = x₀ và y = y₀ vào y = (m – 2)x + 3, ta được:

y₀ = (m – 2)x₀ + 3

$\iff$ mx₀ – 2x₀ + 3 – y₀ = 0

$\iff$ mx₀ – (y₀ + 2x₀ – 3) = 0 (1)

Để (1) luôn đúng với mọi giá trị của m thì .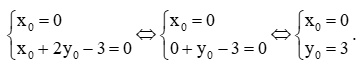

Vậy đồ thị hàm số y = (m – 2)x + 3 luôn đi qua điểm cố định I(0; 3).

Bài 18 trang 20 SBT Toán 8 Tập 2: Cho các đường thẳng d₁: y = x + 1; d₂: y = –x – 3; d₃: y = mx + 2m – 1.

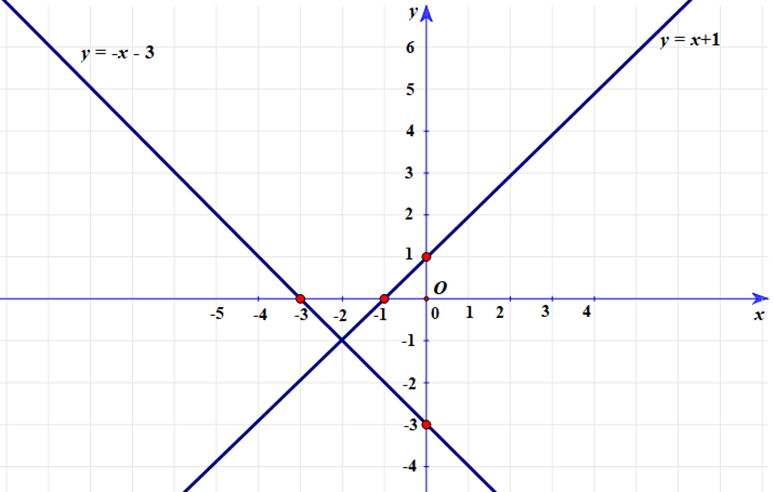
a) Vẽ hai đường thẳng d₁ và d₂ trên cùng một mặt phẳng toạ độ Oxy.

b) Với giá trị nào của m thì đường thẳng d₃ trùng với đường thẳng d₂?

Lời giải:

a) Vẽ hai đường thẳng d₁ và d₂ trên cùng một mặt phẳng toạ độ Oxy.

b) Đường thẳng y = mx + 2m – 1 trùng với đường thẳng y = –x – 3.

Do đó: 

Vậy m = –1 thoả mãn đề bài.

Xem thêm các bài giải SBT Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác: