Cho ∆ABC có AD, BE, CF lần lượt là đường phân giác của góc A, góc B, góc C (D ∈ BC, E ∈ AC, F ∈ AB)

Bài 4.13 trang 52 SBT Toán 8 Tập 1: Cho ∆ABC có AD, BE, CF lần lượt là đường phân giác của góc A, góc B, góc C (D ∈ BC, E ∈ AC, F ∈ AB). Chứng minh rằng: $\frac{AE}{EC}\cdot \frac{CD}{DB}\cdot \frac{BF}{FA}=1.$

Trả lời

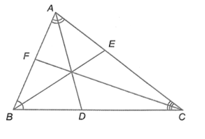
Trong ∆ABC có AD là phân giác của $\widehat{BAC}$ nên $\frac{DC}{DB}=\frac{AC}{AB}$ (tính chất đường phân giác của tam giác).

Tương tự, ta có BE, CF lần lượt là tia phân giác của $\widehat{B},\widehat{C}$.

Suy ra $\frac{EA}{EC}=\frac{BA}{BC};\frac{FB}{FA}=\frac{CB}{CA}$.

Do đó: $\frac{AE}{EC}\cdot \frac{CD}{DB}\cdot \frac{BF}{FA}=\frac{BA}{BC}\cdot \frac{AC}{AB}\cdot \frac{CB}{CA}=1$

Xem thêm các bài giải Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:

Bài 15: Định lí Thalès trong tam giác

Bài 16: Đường trung bình của tam giác

Bài 17: Tính chất đường phân giác của tam giác

Bài tập cuối chương 4

Bài 18: Thu thập và phân loại dữ liệu

Bài 19: Biểu diễn dữ liệu bằng bảng, biểu đồ